[PAT甲级]1020、二叉树层序遍历

题目链接

https://pintia.cn/problem-sets/994805342720868352/exam/problems/994805485033603072

题目描述

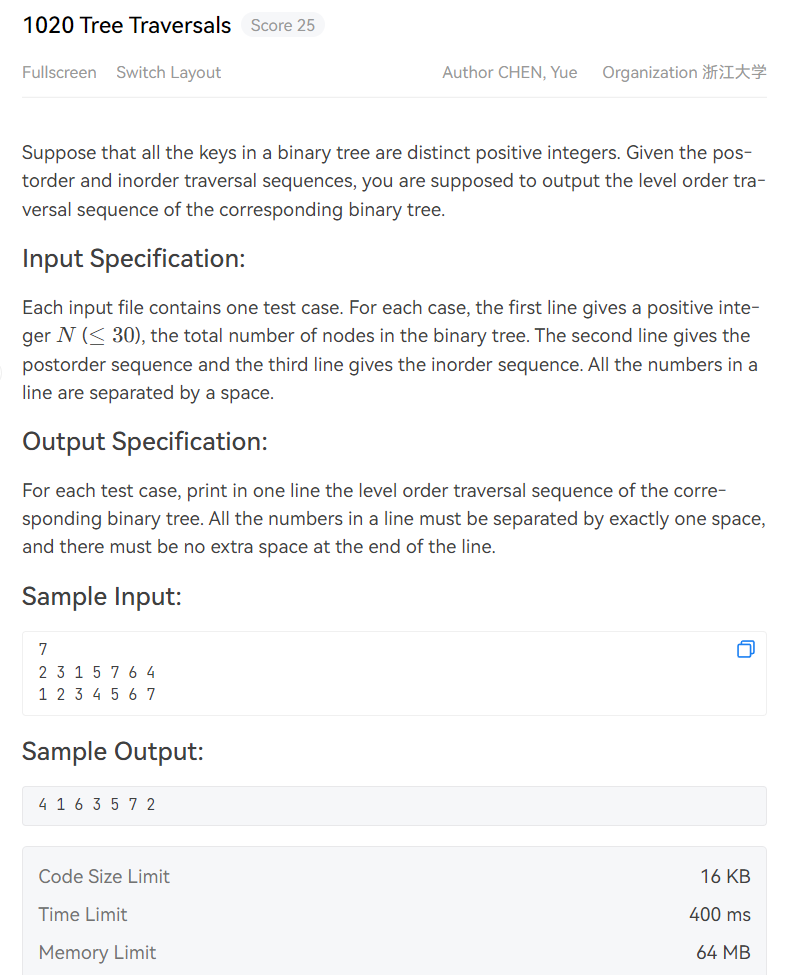
大致意思就是，他会给出三行输入，第一行是这个二叉树有多少个节点，

第二行是这棵二叉树的后序遍历结果，第三行是这棵二叉树的中序遍历结果，要求我们输出这棵树层序遍历的结果。

我的思路

既然是二叉树，并且只给了两种遍历的结果，想要得到层序遍历的结果，我们就需要构建出这棵树，或者是在建立的过程中把每一层的节点保存下来。

我是第一次见这样的题，以前都是直接建树然后宽度优先搜索来进行层序遍历，这次树都不直接给，确实让我头疼了一会= =。

我是先动手推导了一下题目给出的输入样例，每次都是在后序遍历的序列中找到某个区间的最后一个值，它就是这个子树的根节点；有了根节点以后，再去看中序遍历，这个根节点的左边就是它的左子树，右边就是它的右子树，如此类推，循环的进行下去，最后树就建立出来了。

带着这种想法，我觉得可以递归试一下，在递归的过程中把每一层的根节点都收集起来，最后再统一输出。

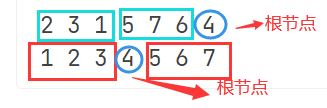
那么可以看到，我们每次看到的子树，它含有的节点会构成一个区间，比如4的左子树里有1，2，3；

接下来如果要找出4的左子树的根节点，那就是要在后序序列中找到1，2，3这三个值构成的区间中的最后一个值，这个例子里1，2，3在后序中的顺序是2，3，1,所以这棵子树的根节点就是1 .

那么每次递归要得出一个根节点，就必须知道这棵子树在后序、中序序列中的区间位置。

所以递归函数定义为：

// s1,e1 分别是后序遍历区间的起始下标和结束下标，后面同理，是中序遍历的 
void dfs(int s1,int e1,int s2,int e2,int level)

递归参数传递

中序的区间对我们来说是已知的，比如4的左子树就是1，2，3，他们的中序下标就是0，1，2，这些从例子里就可以看出。但是后序的区间就不一定了，没有明显的规律。

这时我写的第一版递归就成了死递归，因为递归传递的参数不正确。去看了眼大佬们的思路，也是收获很多，实际上，无论是中序还是后序，他们的区间的长度是一样的，因为是同一棵子树，节点数是一样的，所以区间长度一定相同。由于我们是可以直接写出中序的左右子树区间的，因此只需要观察得出后序的表达式，然后二者相等，就可以求出正确的区间了。

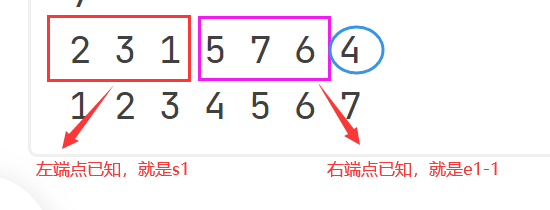
可以看出，左子树在后序遍历中的右端点是不确定的，但左端点就是s1

右子树在后序遍历中的左端点是不确定的，但右端点就是e1-1

假设根节点在中序遍历的下标是index。

那么由中序遍历序列知，左子树的长度 = index - s2，右子树的长度为e2 - index

可列式：

左子树： ？ - s1 = index - 1 - s2
右子树： e1 - 1 - ? = e2 - index - 1

？就是各自未知的那个下标了。

退出条件

由于每次递归进入的子树都是越来越小的，区间越缩越小。

由于中序遍历我们是能明确知道范围的，所以区间下标不会出现左小于右的情况。

但是后序遍历中存在未知的下标，我们是写了表达式让它自己计算的，这就可能出现左端下标小于右端下标，这样必定会出现下标越界的情况。

因此，左端下标小于右端下标就是我们的退出条件。

程序代码

#include<iostream>
#include<vector> 
using namespace std;
int N;
//order[0]代表的是后序，order[1]代表的是中序
vector<int> order[2];
vector<int> tree[31];
int postIndex[31];
int inIndex[31];
int left_length,right_length;

// s1,e1 分别是后序遍历区间的起始下标和结束下标，后面同理，是中序遍历的 
void dfs(int s1,int e1,int s2,int e2,int level){
    if(s1>e1) return;
    // 后序遍历区间的最后一个值一定是这个子树的根节点 
    int result = order[0][e1];
    // 存入树容器对应层里去 
    tree[level].push_back(result);
    // 进入左子树
    // 左子树在后序遍历的区间的右端点未知，要用左端点下标+长度 -1 
    dfs(s1, s1+inIndex[result]-1-s2,s2,inIndex[result]-1,level + 1);
    // 进入右子树,右子树区间在后序遍历的区间的左端点未知，要用右端点下标 -长度
    dfs(inIndex[result]+e1-e2, e1-1 ,inIndex[result]+1,e2,level + 1);
}


int main(){
    int i,j,k,count;
    cin>>N;
    // 存入后序遍历序列 
    for(i=0;i<N;i++){
        cin>>j;
        // 记录这个点在后序序列中的下标 
        postIndex[j] = i; 
        order[0].push_back(j);
    }
    k = j;
    // 存入中序遍历序列 
    for(i=0;i<N;i++){
        cin>>j;
        // 记录这个点在中序序列中的下标
        inIndex[j] = i;
        order[1].push_back(j);
    }
    
    // 后序遍历的最后一个结果一定是总根节点，所以初始下标该节点的中序下标 
    k = inIndex[k];
    dfs(0,N-1,0,N-1,1);
    count = N;
    for(int level=1;level<=N;level++){
        
        for(int i=0;i<tree[level].size();i++){
            if(count!=N) cout<<" ";
            cout<<tree[level][i];
            count--;
        }
    }
    cout<<endl;
    return 0;
}

虽然这题通过率挺高，但是我还是没能一下就想出来，在借鉴了别人的想法以后才成功AC...

菜狗会继续努力