凸优化第九章无约束优化 9.3 梯度下降方法

使君杭千秋

于 2020-12-20 00:03:22 发布

阅读量332

点赞数 2

分类专栏：凸优化

原文链接：https://blog.youkuaiyun.com/wangchy29/article/details/87968905

版权

凸优化专栏收录该内容

62 篇文章

订阅专栏

本文介绍了梯度下降方法，以负梯度为搜索方向，通过直线搜索确定步长。列举了空间的二次、非二次型等问题的例子，对比了回溯搜索和精确搜索方法的迭代过程。指出梯度方法通常近似线性收敛，收敛速度受海瑟矩阵或下水平集条件数影响。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

9.3 梯度下降方法

梯度下降方法
例子

梯度下降方法

用负梯度做搜索方向，即令 $\bigtriangleup x = -\bigtriangledown f(x)$ ，这种下降方法称为梯度下降方法：

给定初始点 $x \in dom(f)$

重复进行

$\bigtriangleup x = - \bigtriangledown f(x)$
直线搜索：通过精确或回溯直线搜索方法确定步长t
修改： $x:=x+t \bigtriangleup x$

直到满足停止条件

停止准则通常取为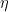： $\begin{Vmatrix} \bigtriangedown f(x)\end{Vmatrix}_2 \leq \eta$ ，其中 $\eta$ 是小正数。一般情况下步骤１１完成后就检验停止条件而不是在修改后才检验。

例子

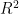空间的二次问题

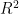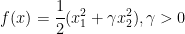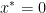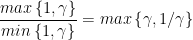
考虑 R^2 上的二次目标函数： $f(x)=\frac{1}{2}(x_1^2+\gamma x_2^2),\gamma >0$ ，显然最优点是 x^*=0 。f的海瑟矩阵是常熟，其特征值是１和 $\gamma$ ，因此起所有下水平集的条件数为 $\frac{max\left \{ 1,\gamma \right \}}{min\left \{ 1,\gamma \right \}}=max\left \{ \gamma,1/\gamma \right \}$

采用精确线性搜索，初始点为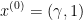 $x^{(0)}=(\gamma,1)$ ，迭代过程中每个点的表达式写成：

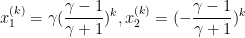
$x_1^{(k)}=\gamma(\frac{\gamma-1}{\gamma+1})^k,x_2^{(k)}=(-\frac{\gamma-1}{\gamma+1})^k$

下图是 $\gamma =10$ 时，精确线性搜索方法的迭代过程，其中虚线是等值线。

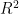空间的非二次型问题

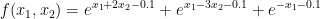
$f(x_1,x_2)=e^{x_1+2x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}$

上图分别是该问题的回溯搜索方法和精确搜索方法的迭代过程。可以看出精确搜索方法的收敛速度大约是回溯收敛方法的两倍。

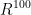$R^{100}$ 空间的一个问题

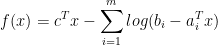
$f(x)=c^Tx-\sum_{i=1}^mlog(b_i-a_i^Tx)$

上图是分别采用回溯直线搜索和精确直线搜索的梯度优化方法所产生的误差和迭代次数之间的关系

梯度方法和条件数的结论

书上给出了一些结论

梯度方法通常呈现近似线性收敛性质
回溯参数 $\alpha ,\beta$ 的取值对收敛性有明显的影响，但不会产生戏剧性的效果。精确搜索方法有时可以改善梯度方法的收敛性，胆效果不是很大。
收敛速度强烈以来与海瑟矩阵或下水平集的条件数。及时问题的条件数不是太坏，收敛速度也可能很慢，如果条件数很大，梯度方法已经慢的失去实用价值。

来源：https://blog.youkuaiyun.com/wangchy29/article/details/87968905

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。