凸优化第九章无约束优化 9.1 无约束优化问题_无约束优化线性方程组的等价求解-优快云博客

9.1 无约束优化问题

例子
强凸性及其含义

无约束优化问题

$minimize \,\, f(x)$ 其中 $f:R^n \rightarrow R$ 是二次可微凸函数（dom(f)是开集），假设该问题可解，存在最优点 x^* ，这里用 p^* 表示最优值 inf_xf(x)=f(x^*) 。

由于f是二次可微凸函数，最优点 x^* 应满足： $\bigtriangledown f(x^*)=0$

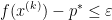所以无约束优化问题的求解变成了求解上述方程的解。一般情况下，必须采用迭代算法求解此方程，即计算点列 $x^{(0)},x^{(1)}\cdots \in dom(f)$ 使得 $k\rightarrow \infty$ 时， $f(x^{(k)})\rightarrow p^*$ ，这样的点列被称为优化问题的极小化点列。当 $f(x^{(k)})-p^* \leq \varepsilon$ 时，算法将终止，其中 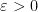$\varepsilon >0$ 是设定的容许误差值。

初始点和下水平集

迭代的方法需要一个适当的初始点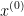 $x^{(0)}$ ，该初始点必须满足两个条件：

初始点必须在dom(f)内
下水平集 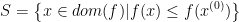$S=\left \{ x \in dom(f)|f(x)\leq f(x^{(0)}) \right \}$ 必须是闭集。

条件１很容易满足，条件２却不容易满足。除非在全部的下水平集都是闭集的时候，条件２才容易满足。

全部下水平集都是闭集的情况：

epi f （ｆ的上境图）是闭集
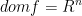
当 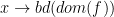$x \rightarrow bd(dom(f))$ ，即x趋于dom(f)的边界时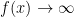， $f(x)\rightarrow \infty$

下水平集的条件数

对任意满足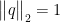 $\begin{Vmatrix}q \end{Vmatrix}_2=1$ 的方向向量q，我们定义凸集 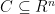$C\subseteq R^n$ 的宽度如下：

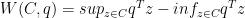
$W(C,q)=sup_{z\in C}q^Tz-inf_{z \in C}q^Tz$

再定义C的最小宽度和最大宽度：

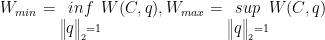
$W_{min}=\underset{\begin{Vmatrix} q\end{Vmatrix}_2=1}{inf}W(C,q), W_{max}=\underset{\begin{Vmatrix} q\end{Vmatrix}_2=1}{sup}W(C,q)$

于是凸集C的条件数可以表示成：

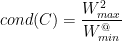
$cond(C)=\frac{W^2_{max}}{W^@_{min}}$

例子

无约束几何规划

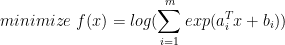
$minimize \, \, f(x)=log(\sum_{i=1}^m exp(a_i^Tx+b_i))$

其最优性条件为：

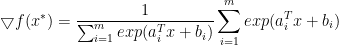
$\bigtriangledown f(x^*)=\frac{1}{\sum_{i=1}^mexp(a_i^Tx+b_i)}\sum_{i=1}^mexp(a_i^Tx+b_i)$

但一般情况下，此方程组没有解析解，于是采用迭代方法，这里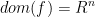 dom(f)=R^n ，所以人和店都可以是初始点。

线性不等式的解析中心

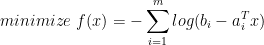
$minimize \, \, f(x)=-\sum_{i=1}^m log(b_i-a_i^Tx)$

其中 $dom(f)=\left \{ x|a_i^Tx<b_i,i=1,\cdots m\right \}$

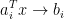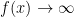采用迭代的方法，也可以找到初始点，因为当 $a_i^Tx\rightarrow b_i$ 时， $f(x)\rightarrow \infty$ ，满足下水平集为闭集的条件。

强凸性及其含义

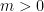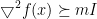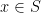假设目标函数在Ｓ上是强凸的，这是指存在 m>0 使得 $\bigtriangledown^2 f(x)\succeq mI$ ，对任意的 $x \in S$ 都成立。

对于任意的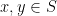 $x,y \in S$ 都有 $f(y)=f(x)+\bigtriangledown f(x)^T(y-x)+1/2(y-x)^T\bigtriangledown ^2f(z)(y-x),z \in [x,y]$

由强凸性可推出

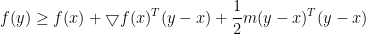
$f(y) \geq f(x)+\bigtriangledown f(x)^T(y-x)+\frac{1}{2}m(y-x)^T(y-x)$

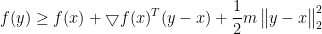
$f(y) \geq f(x)+\bigtriangledown f(x)^T(y-x)+\frac{1}{2}m\begin{Vmatrix} y-x\end{Vmatrix}_2^2$

可知，对固定的x，不等式右边是y的二次凸函数，记为Ｌ，令其对y的一阶导数为０

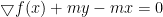
$\bigtriangledown f(x)+ my-mx=0$

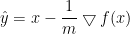
$\hat{y}=x-\frac{1}{m}\bigtriangledown f(x)$

可知Ｌ的最小值为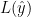 $L(\hat{y})$ ，所以可推出

$f(y) \geq f(x)+\bigtriangledown f(x)^T(y-x)+\frac{1}{2}m\begin{Vmatrix} y-x\end{Vmatrix}_2^2\geq L(\hat{y})=f(x)+\bigtriangledown f(x)^T(-\frac{1}{m}\bigtriangledown f(x))+\frac{1}{2}m\begin{Vmatrix}-\frac{1}{m}\bigtriangledown f(x)\end{Vmatrix}_2^2=f(x)-\frac{1}{2m}\begin{Vmatrix}\bigtriangledown f(x)\end{Vmatrix}_2^2$

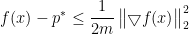
由于y是任意的，又可推出 $p^*\geq f(x)-\frac{1}{2m}\begin{Vmatrix}\bigtriangledown f(x)\end{Vmatrix}_2^2$ 即 $f(x)-p^*\leq \frac{1}{2m}\begin{Vmatrix}\bigtriangledown f(x)\end{Vmatrix}_2^2$