7.3 最优检测器设计及假性检验
二值假设检验
- 检测问题
- 随机检测器
- 检测概率矩阵
- 检测器设计的多准则表述
- 标量化
检测问题:
假设X是随机变量,在 中取值,其概率密度分布和参数
中取值,其概率密度分布和参数 的取值有关,对
的取值有关,对 的m个可能值,X的概率密度分布可以由矩阵
的m个可能值,X的概率密度分布可以由矩阵 表征,其元素为:
表征,其元素为: ,即矩阵的第j列对于参数值
,即矩阵的第j列对于参数值 的概率分布。
的概率分布。
对 的m个可能值称为m个假设,我们需要从假设中猜想哪个是正确的,这个问题称为假设检验,而假设检验也可以看成观测到X的某个取值,然后判断不寻常事件(某种假设为一种常规事件,而其他假设均对应不寻常事件)是否发生,如果发生了,是哪一个不寻常事件。于是假设检验问题又称为检测问题。
的m个可能值称为m个假设,我们需要从假设中猜想哪个是正确的,这个问题称为假设检验,而假设检验也可以看成观测到X的某个取值,然后判断不寻常事件(某种假设为一种常规事件,而其他假设均对应不寻常事件)是否发生,如果发生了,是哪一个不寻常事件。于是假设检验问题又称为检测问题。
二值假设检验,即一种特殊的检验问题,即m=2,只有两个假设。这里X是随机变量,且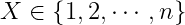 ,假设1:X由概率密度分布
,假设1:X由概率密度分布 产生;假设2:X由概率密度分布
产生;假设2:X由概率密度分布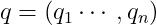 产生;
产生;
随机检测器
随机检测器可以定义为一个矩阵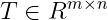 ,其元素为
,其元素为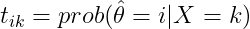 ,其中
,其中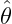 是
是 的猜想值,k是X的观测值。T可以理解为,如果我们得到观测值X=k,那么检测器以概率
的猜想值,k是X的观测值。T可以理解为,如果我们得到观测值X=k,那么检测器以概率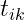 给出估计值
给出估计值 。显然T满足两个约束,
。显然T满足两个约束,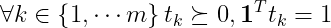 。
。
在二值假设检验中:如果观测到X=k,估计假设1的概率为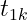 ,估计假设2的概率为
,估计假设2的概率为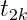 。
。
如果矩阵T的元素要么是0,要么是1,则矩阵T是确定性检测器。
检测概率矩阵
定义检测矩阵D=TP,于是有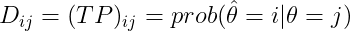 ,即
,即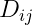 是当
是当 时,猜想为
时,猜想为 的概率。
的概率。
二值假设检验中:
![D =[Tp \, \, Tq]=\begin{bmatrix} 1-P_{fp} &P_{fn} \\ P_{fp} & 1-P_{fn} \end{bmatrix}](https://i-blog.csdnimg.cn/blog_migrate/c9864256642b0f575d385a9b82cd4570.gif)
其中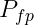 表示X是由分布p产生但却被估计为假设2(由分布q产生)的概率,
表示X是由分布p产生但却被估计为假设2(由分布q产生)的概率,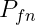 表示X是由分布q产生但却被估计为假设1(由分p产生)的概率。
表示X是由分布q产生但却被估计为假设1(由分p产生)的概率。
检测器设计的多准则表述
对于二值假设检验问题,检测器设计的目标就是极小化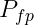 和
和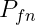 ,即
,即
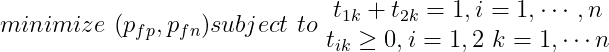
而对于一般的假设检验,检测器设计的目标是极小化 ,即
,即
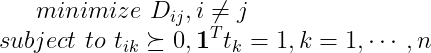
标量化
对于二值假设检验问题的标量化,即加上一个惩罚权重,即:
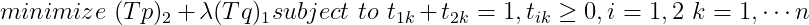
其中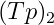 表示列向量Tp的第2行的元素。
表示列向量Tp的第2行的元素。
解析解:
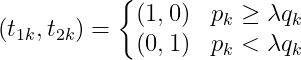
对于一般的假设检验问题的标量化,即引入权系数将目标函数加权求和,即
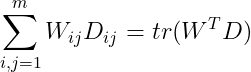
其中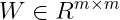
检验问题等价于:
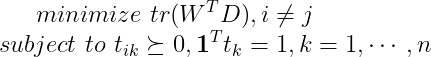
目标函数还可以描述为一系列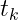 的线性函数的和:
的线性函数的和:
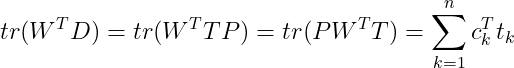
其中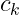 是
是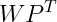 的第k列。
的第k列。
于是可以通过分别求解下面的线性规划来求解检验问题。
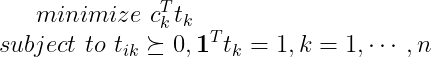
极小极大检测器
对于二值假设检验,极小极大检测器,即求解:
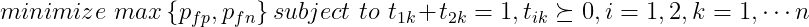
来源:https://blog.youkuaiyun.com/wangchy29/article/details/87465799

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








