本文仅提供第(1)问的模型及代码 (Ps:其实是之前没写第二问)
题目
试就某市设置交巡警服务平台的相关情况,建立数学模型分析研究下面的问题:
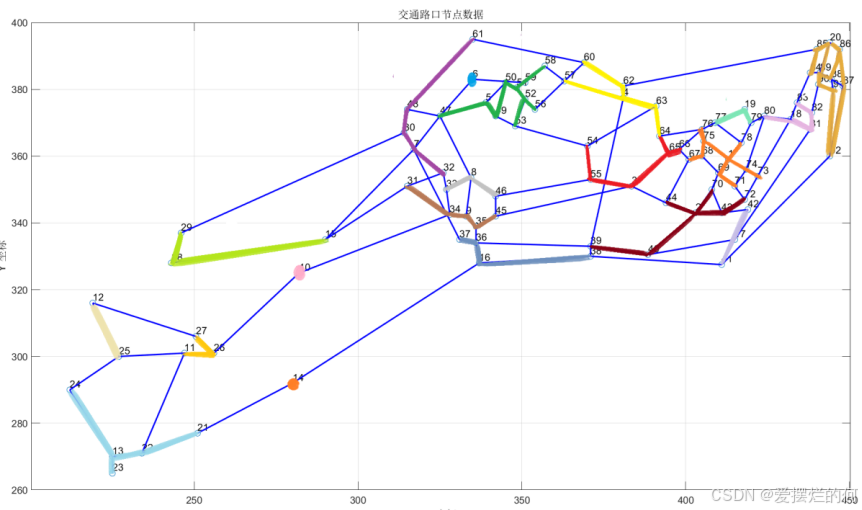
(1)附件1中的附图1给出了该市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图,相关的数据信息见附件2。请为各交巡警服务平台分配管辖范围,使其在所管辖的范围内出现突发事件时,尽量能在3分钟内有交巡警(警车的时速为60km/h)到达事发地。
对于重大突发事件,需要调度全区20个交巡警服务平台的警力资源,对进出该区的13条交通要道实现快速全封锁。实际中一个平台的警力最多封锁一个路口,请给出该区交巡警服务平台警力合理的调度方案。
根据现有交巡警服务平台的工作量不均衡和有些地方出警时间过长的实际情况,拟在该区内再增加2至5个平台,请确定需要增加平台的具体个数和位置。
模型准备
我们需要使用Floyd算法求解从服务平台到各路口的最短路径,matlab代码如下
TT=readtable("C:\Users\何YJ\Desktop\cumcm2011B附件2_全市六区交通网路和平台设置的数据表.xls",'Sheet','Sheet1','Range','A2:G140');
a=[];b=[];c=[];
a=TT.Var1;
b=TT.Var4;
c=TT.Var7;
g=zeros(92,92);p=zeros(92,92);
for i=1:92
for j=1:92
if i~=j
g(i,j)=10000;
end
end
end
for i=1:139
g(a(i),b(i))=c(i);
end
for i=1:92
for j=1:92
if i>j&&g(i,j)~=10000
g(j,i)=g(i,j);
elseif i<j&&g(i,j)~=10000
g(j,i)=g(i,j);
end
end
end
for i=1:92
for j=1:92
p(i,j)=j;
end
end
for k=1:92
for i=1:92
for j=1:92
if g(i,j)>g(i,k)+g(k,j)
g(i,j)=g(i,k)+g(k,j);
p(i,j)=p(i,k);
end
end
end
end
g=g/10;
符合说明

模型一
为确保各平台工作量分配均衡并提升整体效率,我们构建了一个基于工作量的方差模型
目标: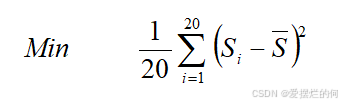
约束条件:
(1)“0-1”变量约束

(2)单一路口平台管辖约束
一个路口只能被一个交巡警服务平台所管辖
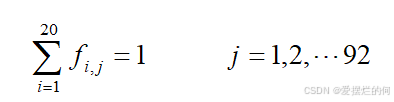
(3)就近分配
由于部分交巡警服务平台直接安置在路口处,对于这些路口,我们直接将其分配给相对应的交巡警服务平台进行管辖
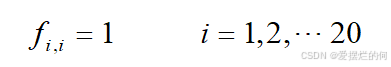
(4)力争三分钟内抵达案发地点
我们发现所有平台都无法在3分钟内抵达的路口只有28,29,38,39,61,92这六个路口。在这种情况下,我们将采用就近原则,选择距离这六个路口最近的交巡警服务平台进行警力分配。
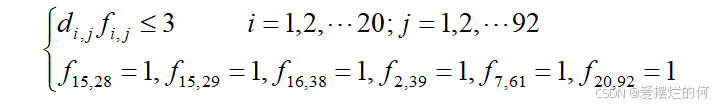
具体模型
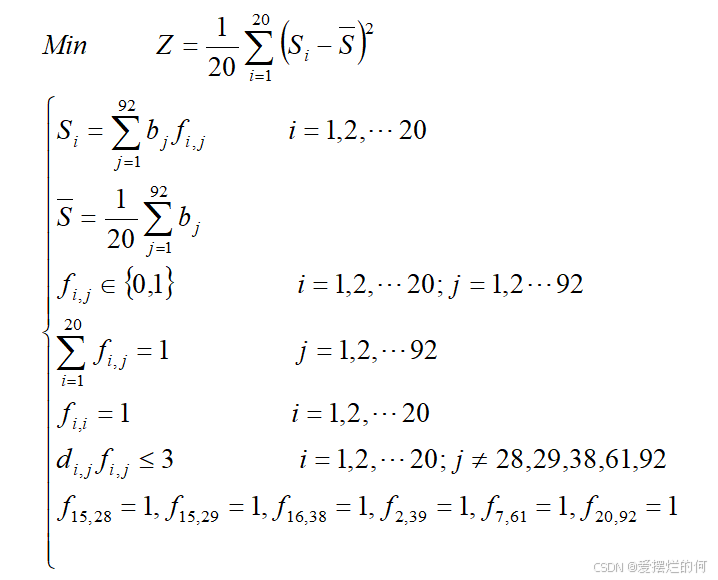
结果
模型二
目标: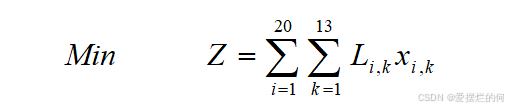
约束条件:
具体模型:
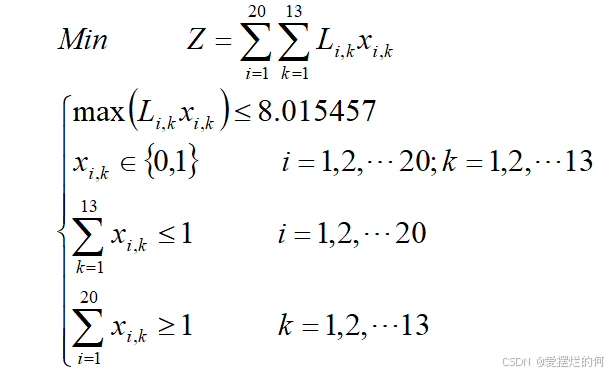
结果
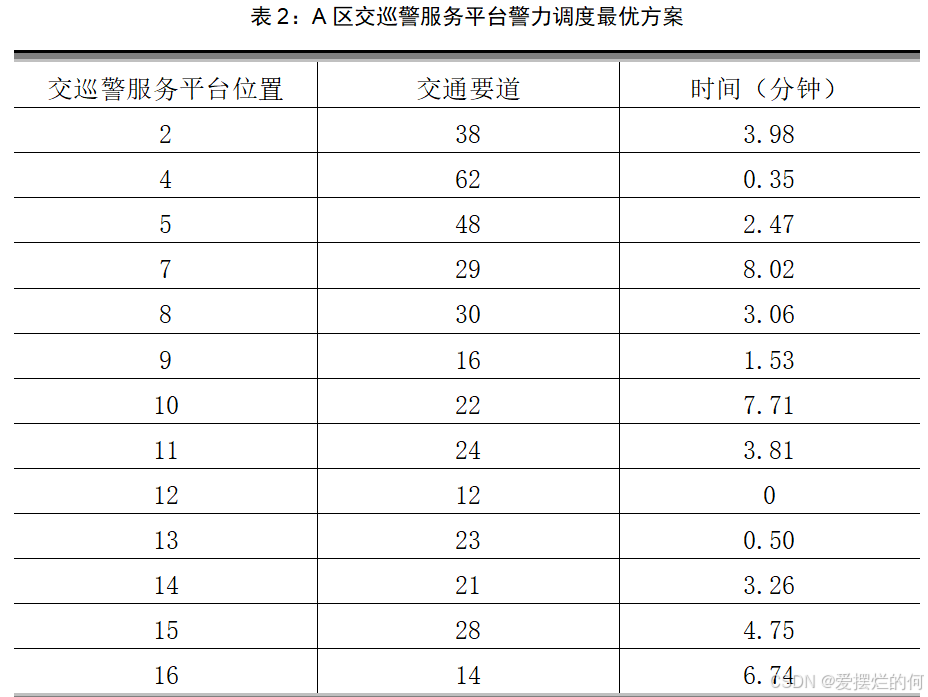
模型三
目标:
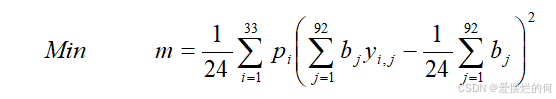
约束条件:


具体模型:
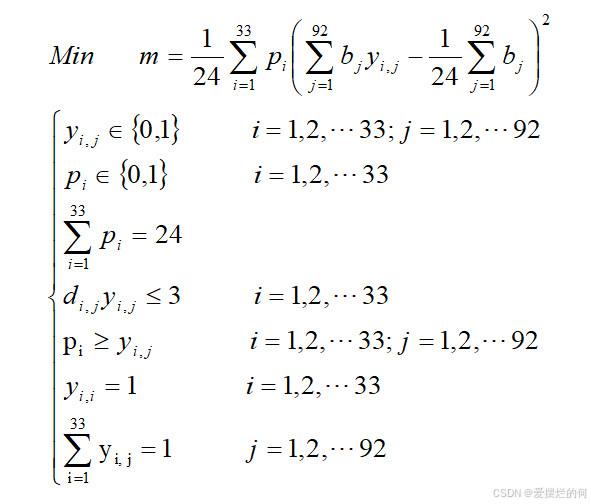
结果:

本文到此结束。注意:本文中的所有模型均可以改进,希望同学们可以在此基础上想出更好的模型
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








