微分方程

4.1 秘籍内容

前人的不断探索，才有现在的好功夫，但是我们学习同时懂得创新。
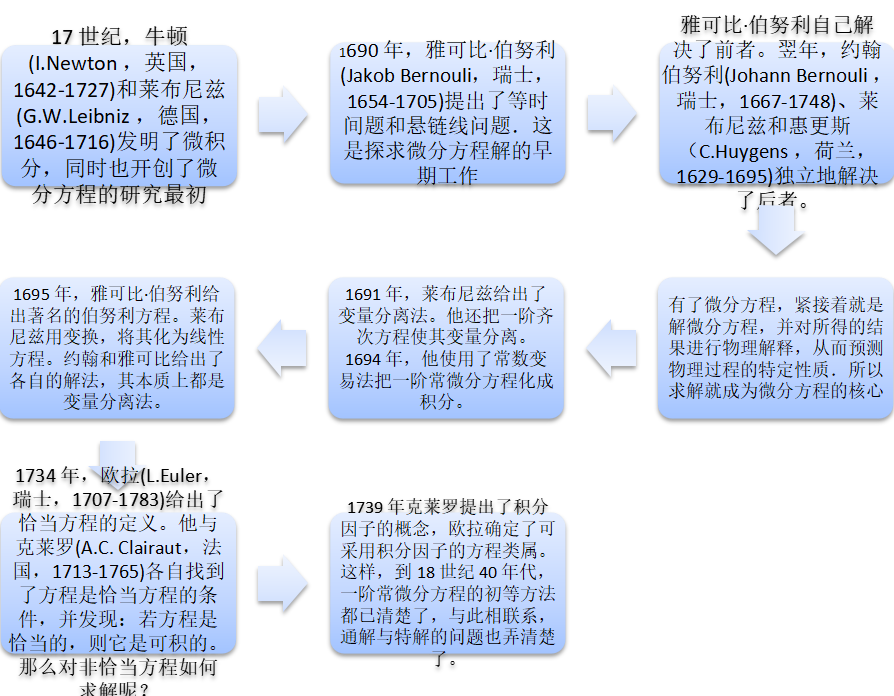
此功夫在科技、工程、经济管理以及生态、环境、人口、交通等各个领域大有作为，因为是研究函数变化规律的有力工具。不过要注意的是一般在用到该功夫可以通过三个方面大大提高效果：
1、根据规律建模；
2、用微元法建模；
3、用模拟近似法建模。

4.2 场景一 ：根据规律建模类模型

在数学、物理、化学等学科有许多实践检验的规律和定律，这些都涉及某些函数变化率。我们可以就此列出相应的微分方程。

例1 物体在空气中的冷却速度与物体和空气的温差成正比，如果物体在20min内由100℃冷却到60℃，那么经过多长时间此物体的温度讲达到30℃？
解：牛顿冷却定律是：将温度为T的物体放入处于常温$T_0$的介质中时，$T$的变化率正比于TT