实现折半查找(数据结构与算法 - 查找)

最新推荐文章于 2022-05-12 23:51:11 发布

原创

最新推荐文章于 2022-05-12 23:51:11 发布 · 5.5k 阅读

51 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #c语言 #c#

本文详细介绍了折半查找算法在顺序存储线性表中的应用，包括关键码的查找、插入、删除等操作，提供了具体的C语言实现代码，适用于初学者理解折半查找的基本原理及其实现细节。

相关知识

折半查找通常是针对顺序存储的线性表，线性表的结点按关键码从小到大排序，后面称之为折半查找的顺序表。为了简化讨论，假设折半查找的顺序表中每个结点只含一个关键码，关键码为整数。图 1 给出了一个存储了 4 个关键码的折半查找的顺序表的存储结构图。
下面描述了线性表顺序存储的一种实现方案。该实现方案的示意图为：
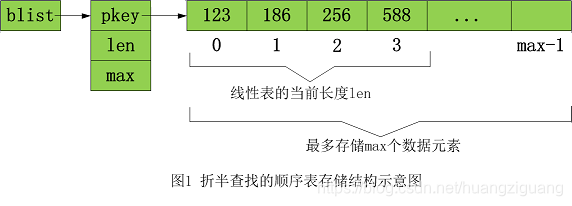
在这里插入图片描述
指针pkey是存储关键码的连续空间的起始地址，顺序表中当前的关键码的个数由len给出，该顺序表中最多可存储max个关键码。
将pkey、len、max组织成一个结构，该结构定义为：

struct BSeqList
{
   
   
    int* pkey;  // 指向关键码数组的指针
    int len;  // 当前元素个数
    int max;  // 线性表的最大元素数
};

只要给定指向该结构的一指针blist，就可对线性表进行操作。
对折半查找的顺序表定义如下操作，各个操作函数的功能详见下面给出的代码文件 BSlist.cpp 的代码框架：

BSeqList* BSL_Create(int size);
void BSL_Free(BSeqList* blist);
int BSL_InsKey(BSeqList* blist, int key);
int BSL_FindKey(BSeqList* blist, int key);
int BSL_DelKey(BSeqList* blist, int key);
void BSL_Print(BSeqList* blist);

输入输出格式说明
输入格式：
首先输入一个正整数max，创建一个最多可存储max个元素的表。
然后输入多个操作：如果输入 “insert” ，则后面跟一个数x，表示将x插入；如果输入 “delete” ，则后面跟一个数x，表示将x删除；如果输入 “end” ，表示输入结束。
输出格式：
输出表的长度，然后从表头到表尾依次输出各元素。
以下是平台对 step1/Main.cpp 的样例测试集：
样例输入：

9
insert 9
insert 8
insert 89
insert 11
insert 22
insert 13
delete 11
delete 5
end

样例输出：

list length: 5
The list contains: 8  9  13  22  89

//折半查找的顺序表 实现文件
//每个结点的数据是关键码
////////////////////////////

最低0.47元/天解锁文章