6_Visibility Graph_宾夕法尼亚大学机器人运动规划专项课程【学习笔记】

现在有一个理论框架，可以(以此切入)考虑大面积的运动规划问题，如何在位形空间中规划路径，下面来探讨一下该问题的三种不同解法，它们的出发点是一样的
也就是，一开始它们都将(机器人的)运动放到连续位形空间里进行规划，然后用不同的方法在图像中对问题进行重构，于是我们就可以应用讨论过的算法，如烧草、Dijikstra 和 A* 算法，我们可以用接下来的图中呈现的2D规划方案来阐明这些方法。

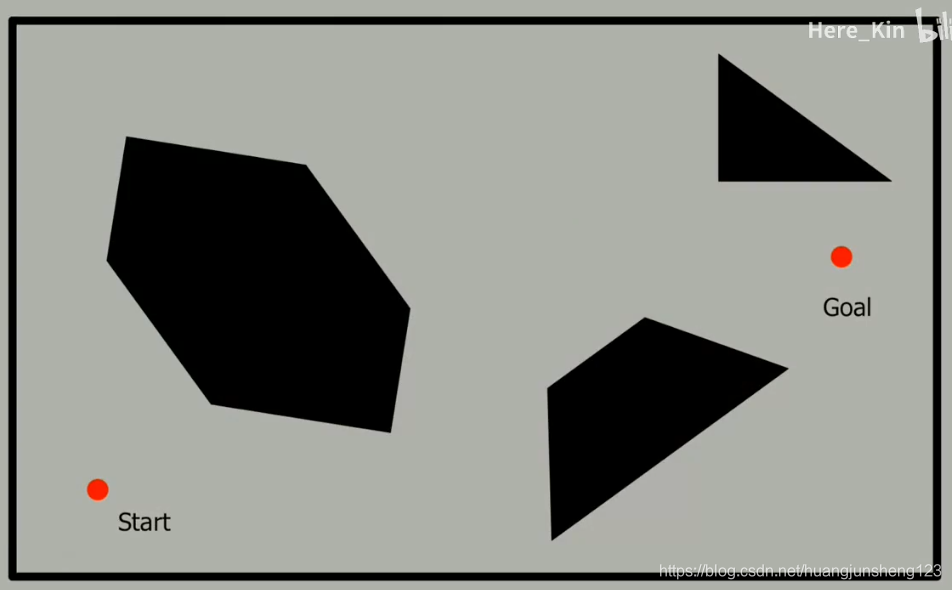
像往常样，我们的目标是，在二维的位形空间内找到一个从起点到终点的轨迹，在这个例子中，位形空间中的障碍物被简化成多边形，表明将出现离散化的现象。

如下图所示，我们将(起始)点和每个位形空间光学顶点(optical vertex)两两相连，然后，我们只需要计算这个可视图(visibility graph)(中的数据)。
具体地说，我们在任意两个顶点之间绘制一条边，这两个点可用直线连接，而且这些直线完全处于自由空间，注意，同个障碍上的相邻顶点间的边也包括在内。【这里感觉官方课件中少画了一条边，所以用红色双向箭头补上】

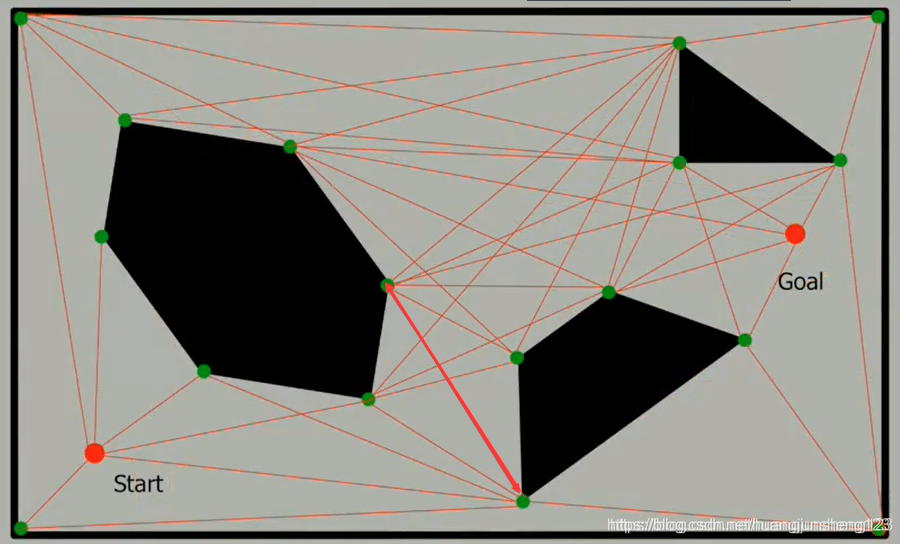
为了能够让算法运作起来，我们需要确定，在位形空间中任何两点之间的线与障碍是否相交，在此图中的位形空间，其障碍是多边形的，实际上(对于算法的运行）是相对简单的，在这个图中，我们把起点和终点也算作(需要描绘的)点。

完成这一步后,让我们回到一开始讨论的的规划问题中，我们的目标是，建立一条从起点到终点的最短路径，解决这个问题很简单用Dijkstra算法就行，这里是这个例子中我们所找到的最短路径的结果。