机器学习之数学基础：方差的性质以及常见分布的方差

本文重点

在数据分析和概率统计中，方差是衡量随机变量离散程度的核心指标。它不仅揭示了数据围绕均值的波动规律，更在金融风险评估、质量控制、机器学习等领域发挥着关键作用。

方差的性质

• 设c是常数, 则 Var(c) = 0
• 若 k 是常数，则 Var(kX) = k²Var(X)，这个性质说明了将随机变量的取值扩大k倍，那么方差就会扩大k²倍。
• 若X1与X2 相互独立，则Var(X1±X2) = Var(X1) +Var(X2)，注意只有加没有减了，可推广为：若X1, X2, …, Xn相互独立，则：

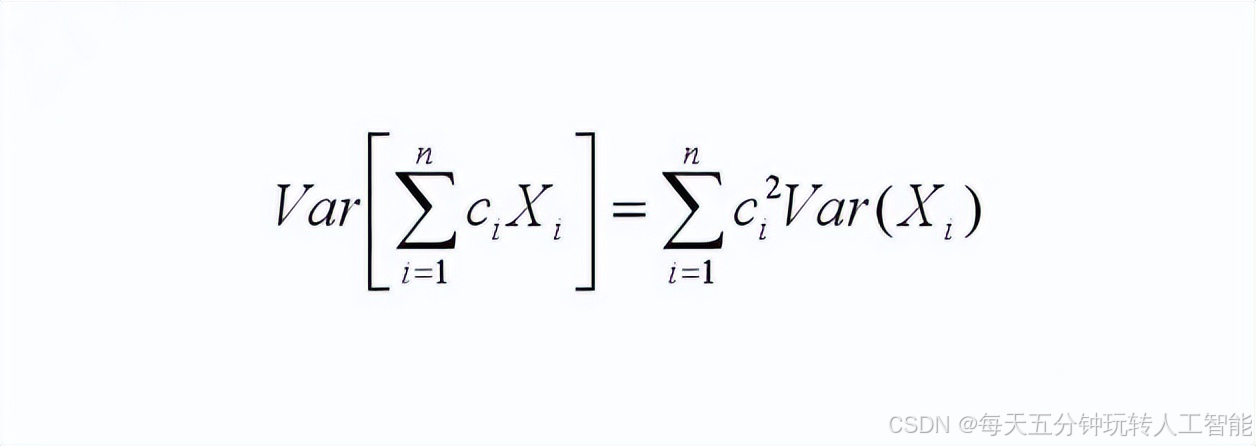
• Var(X) = 0 P{X= c }=1，这里 c = E(X)。这个意思是说若方差为0，那么这个随机变量恒等于c，然后均值也是c

常见分布的方差

两点分布

若 X ~ B(1, p)，则 Var(X) = p(1-p)

二项分布

若 X ~ B(n, p)，则 Var(X) = n p(1-p)

泊松分布

若 X ~ P(λ)，则 Var(X) = λ