每天五分钟机器学习：神经网络和支持向量机的基础——感知机模型

本文重点

感知机模型是神经网络和支持向量机的基础。感知机是二分类的线性分类模型 ，它将学习出一个分类超平面，超平面一边是正类样本，而另外一边是负类样本。

具体来说感知机需要学习到的模型函数为w.x+b=0,w.x+b是一个超平面，其中w是超平面的法向量，而b是超平面的截距,当w.x+b>0时，此时样本x表示为正样本，当w.x+b<0时，此时样本为负样本。

感知机由输入空间到输出空间的函数如下：

f（x）=sign（w.x+b）

w和b都是感知机的参数，sign是符号函数，也就是

 

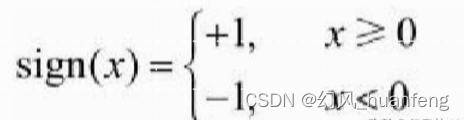
也就是说只要x大于0，此时sign(x)=1，要是x<0,此时sign(x)=0

那么如何才能对于给定样本学习到一个很好的感知机模型呢？和所有的机器学习方法一样，我们需要定义损失函数，在感知机中，损失函数为误分类点到超平面S的总距离，首先注意一点不是所有的点，而是误分类点，我们的目的就是使得所有误分类点的总距离最小，这就是我们的优化目标。

当所有的误分类点到超平面的距离为0的时候，那么就可以说全部样本分类正确

损失函数

输入空间中任意一点x0到超平面S的距离为：