每天五分钟机器学习：为什么局部下降最快的方向是梯度的负方向？

本文重点

在前面的课程中我们学习了梯度下降算法，我们可以看到梯度下降算是沿着负梯度的方向，那么为什么要沿着负梯度的方向呢？本文我们对其将进行详细的解释。

简单理解

梯度下降是一种优化算法，用于最小化损失函数。在每一步迭代中，算法会根据当前位置的梯度方向（即损失函数在该点处的导数）来更新参数。因为导数表示了函数在该点处的变化率，所以朝着负梯度方向更新参数可以使得损失函数在下一步迭代中尽可能减少。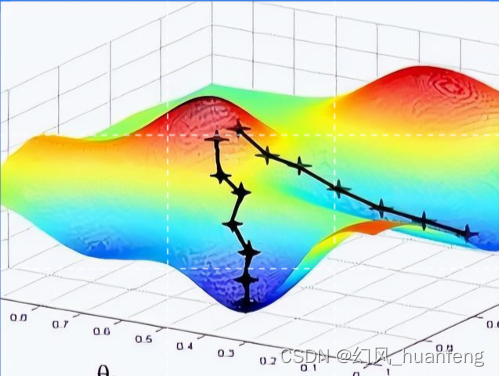

简单来说，朝着负梯度方向更新参数可以让我们走向损失函数下降最快的方向，从而更快地找到最优解。也就是最快下山的方向。

梯度方向和负梯度方向以及步长

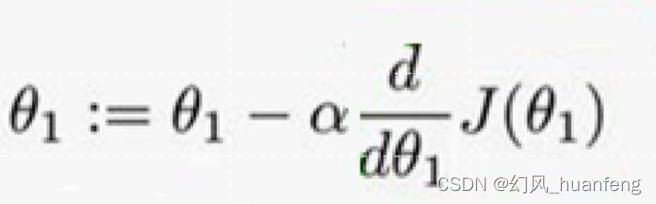
dJ(θ1)/dθ1可以认为是梯度方向

-dJ(θ1)/dθ1可以认为是负梯度方向

从公式角度来说，梯度下降确实是让模型参数更新永远是沿着负梯度的方向

a是学习率，也就是步长，就是说我们在这个负梯度方向走多远

方向有了步长有了，按照这个方向走出指定步长，这就是梯度下降算法的直观理解。

从数学入手