【C++ 真题】P5018 [NOIP 2018 普及组] 对称二叉树

P5018 [NOIP 2018 普及组] 对称二叉树

题目背景

NOIP2018 普及组 T4

题目描述

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

1. 二叉树；
2. 将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

下图中节点内的数字为权值，节点外的 $id$ 表示节点编号。

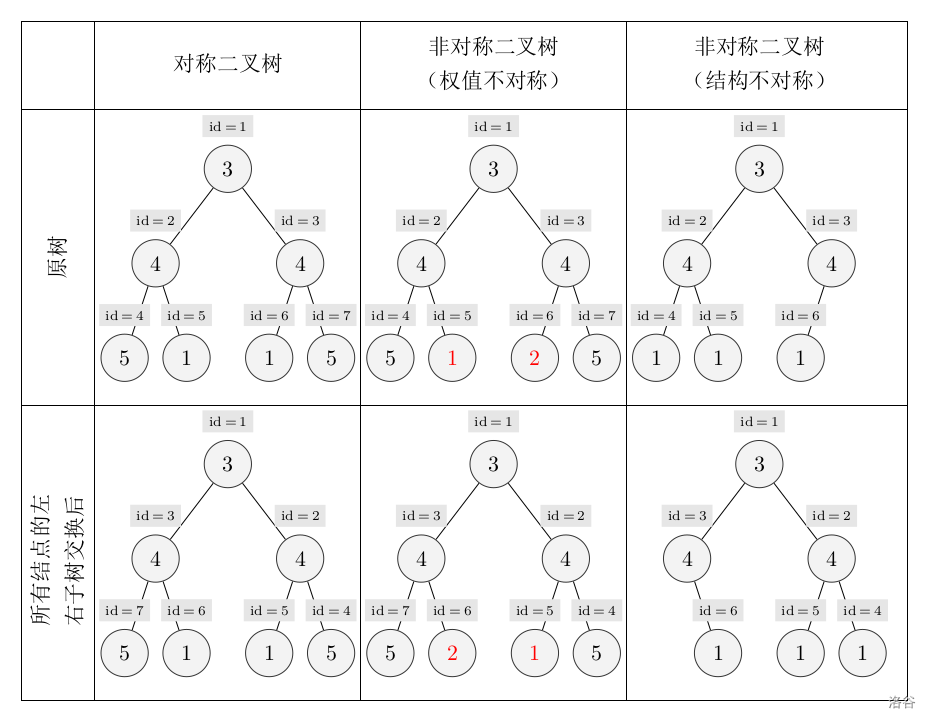
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点 $T$ 为子树根的一棵“子 树”指的是：节点$T$ 和它的全部后代节点构成的二叉树。

输入格式

第一行一个正整数 $n$，表示给定的树的节点的数目，规定节点编号 $1\sim n$，其中节点 $1$ 是树根。

第二行 $n$ 个正整数，用一个空格分隔，第 $i$ 个正整数 $v_i$ 代表节点 $i$ 的权值。

接下来 $n$ 行，每行两个正整数 $l_i,r_i$，分别表示节点 $i$ 的左右孩子的编号。如果不存在左 / 右孩子，则以 $-1$ 表示。两个数之间用一个空格隔开。

输出格式

输出文件共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

输入输出样例 #1

输入 #1

2 
1 3 
2 -1 
-1 -1

输出 #1

1

输入输出样例 #2

输入 #2

10 
2 2 5 5 5 5 4 4 2 3 
9 10 
-1 -1 
-1 -1 
-1 -1 
-1 -1 
-1 2 
3 4 
5 6 
-1 -1 
7 8

输出 #2

3

说明/提示

样例 1 解释

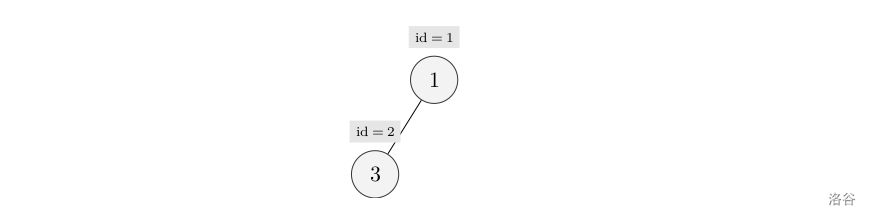
最大的对称二叉子树为以节点 $2$ 为树根的子树，节点数为 $1$。

样例 2 解释

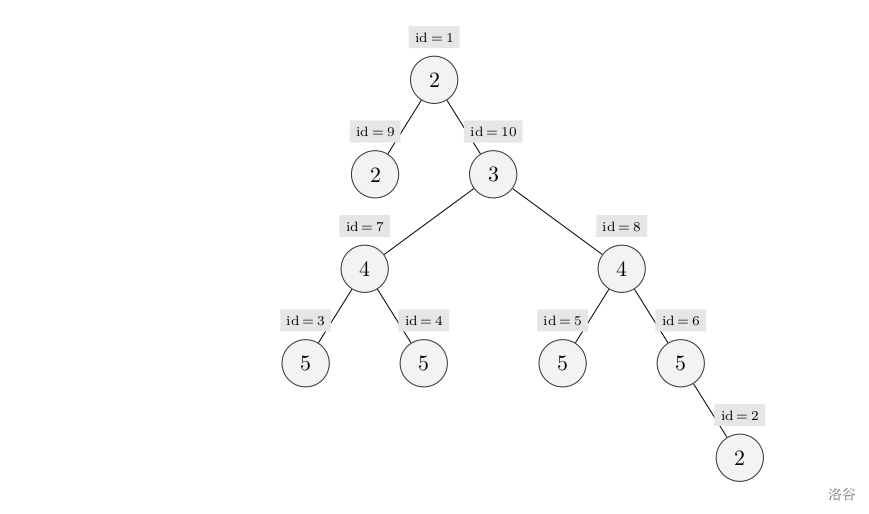
最大的对称二叉子树为以节点 $7$ 为树根的子树，节点数为 $3$。

数据规模与约定

共 $25$ 个测试点。

$v_i\le 1000$。

• 测试点 $1\sim 3,n\le 10$，保证根结点的左子树的所有节点都没有右孩子，根结点的右 子树的所有节点都没有左孩子。
• 测试点 $4\sim 8,n\le 10$。
• 测试点 $9\sim 12,n\le 10^5$，保证输入是一棵“满二叉树” 。
• 测试点 $13\sim 16,n\le 10^5$，保证输入是一棵“完全二叉树”。
• 测试点 $17\sim 20,n\le 10^5$，保证输入的树的点权均为 $1$。
• 测试点 $21\sim 25,n\le 10^6$。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 $1$。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为 $h$，且二叉树有 $2^h-1$ 个节点，这就是满二叉树。

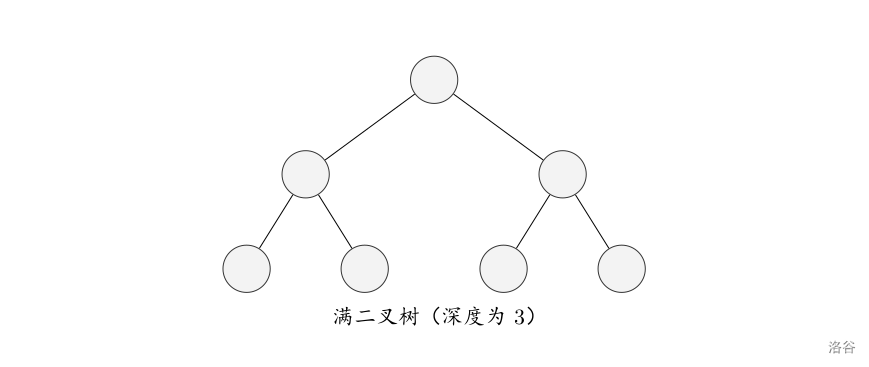
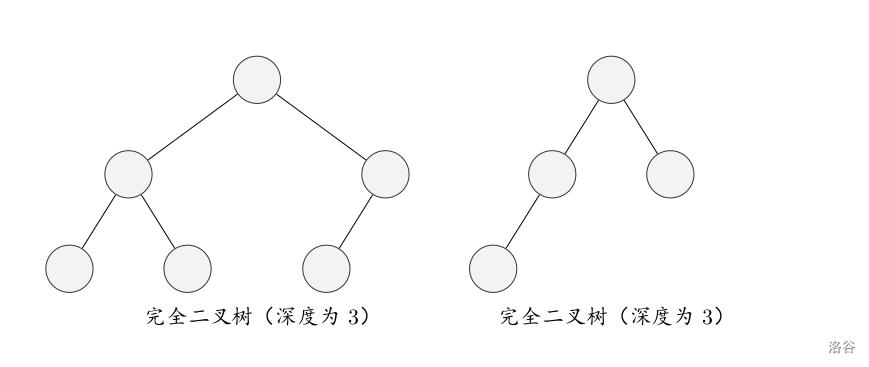
完全二叉树：设二叉树的深度为 $h$，除第 $h$ 层外，其它各层的结点数都达到最大 个数，第 $h$ 层所有的结点都连续集中在最左边，这就是完全二叉树。

题解

#include "bits/stdc++.h"
using namespace std;
const int N = 1e6+7;
int n, maxn = 1, s[N];
struct Node{//节点权重,左右子节点编号
    int l, r, v;
}a[N];

bool issame(int x, int y){// 以x为节点的子树是否对称
    // int ll = a[x].l, rr = a[x].r;
    if(x == -1 && y == -1) {//x没有子节点,是对称的
        return true;
    }
    if(x == -1 || y == -1) return false;//只有一端有子节点,不对称
    if(a[x].v != a[y].v) {//左右子节点权重不同,不对称
        return false;
    }
    if(issame(a[x].l, a[y].r) && issame(a[x].r, a[y].l)) return true;
    //左子树的左子树 vs 右子树的右子树，左子树的右子树 vs 右子树的左子树
    return false;
}

int size(int x){//以x为节点的子树大小
    if(x == -1) return 0;
    return 1 + size(a[x].l) + size(a[x].r);
}

void dfs(int x){
    if(x == -1) return ;
    if(issame(a[x].l, a[x].r)) {
        maxn = max(maxn, size(x));
    }
    dfs(a[x].l);
    dfs(a[x].r);
}

int main(){
    cin>>n;
    for(int i=1;i<=n;++i) cin>>a[i].v;
    for(int i=1;i<=n;++i) cin>>a[i].l>>a[i].r;
    dfs(1);
    cout<<maxn<<endl;
    return 0;
}