一、控制结构
(一)输出斐波拉契数
- 斐波拉契数列,又称黄金分割数列,指的是这样一个数列: 1 、 1 、 2 、 3 、 5 、 8 、 13 、 21 、 34 、 … … 1、1、2、3、5、8、13、21、34、…… 1、1、2、3、5、8、13、21、34、……在数学上,斐波拉契数列以递推的方法定义: F ( 0 ) = 1 , F ( 1 ) = 1 , F ( n ) = F ( n − 1 ) + F ( n − 2 ) ( n ≥ 2 , n ∈ N ∗ ) F(0)=1,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*) F(0)=1,F(1)=1,F(n)=F(n−1)+F(n−2)(n≥2,n∈N∗)在现代物理、准晶体结构、化学等领域,斐波拉契数列都有直接的应用,为此,美国数学会从 1963 1963 1963年起出版了以《斐波拉契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
1、利用简单变量迭代输出斐波拉契数列
- 源代码
#include "stdio.h"
void main()
{
int i, a, b, c;
a = 1;
b = 1;
printf("%-8d %-8d ", a, b);
for (i = 3; i <= 40; i++)
{
c = a + b;
printf("%-8d ", c);
a = b;
b = c;
if (i % 5 == 0)
printf("\n");
}
}
- 运行结果
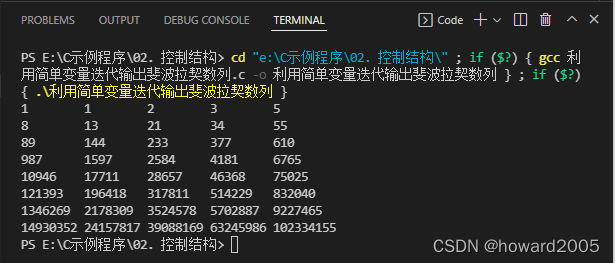
2、利用一维数组递推输出斐波拉契数列
- 源代码
#include "stdio.h"
int main()
{
int i, f[40];
f[0] = 1;
f[1] = 1;
for (i = 2; i < 40; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
for (i = 0; i < 40; i++)
{
printf("%-8d ", f[i]);
if ((i + 1) % 5 == 0)
printf("\n");
}
return 0;
}
- 运行结果
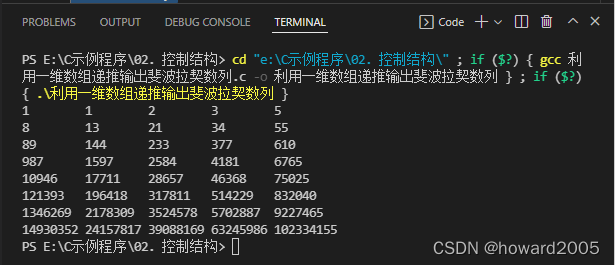
(二)打印杨辉三角形
-
杨辉三角,是二项式系数在三角形中的一种几何排列,中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623 ~ 1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。

-
( a + b ) 1 = a + b (a+b)^1=a+b (a+b)1=a+b
-
( a + b ) 2 = a 2 + 2 a b + b 2 (a+b)^2=a^2+2ab+b^2 (a+b)2=a2+2ab+b2
-
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 (a+b)^3=a^3+3a^2b+3ab^2+b^3 (a+b)3=a3+3a2b+3ab2+b3
-
( a + b ) 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 a b 3 + b 4 (a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4 (a+b)4=a4+4a3b+6a2b2+4ab3+b4
…… -
源代码
#include "stdio.h"
int main()
{
int i, j, k, m[14][14];
for (i = 0; i < 14; i++)
{
for (j = 0; j < 15; j++)
{
m[i][j] = 1;
}
}
for (i = 2; i < 14; i++)
{
for (j = 1; j < i; j++)
{
m[i][j] = m[i - 1][j - 1] + m[i - 1][j];
}
}
for (i = 0; i < 14; i++)
{
for (k = 1; k < 40 - 3 * i; k++)
{
printf(" ");
}
for (j = 0; j <= i; j++)
{
printf("%-5d ", m[i][j]);
}
printf("\n");
}
return 0;
}
- 运行结果
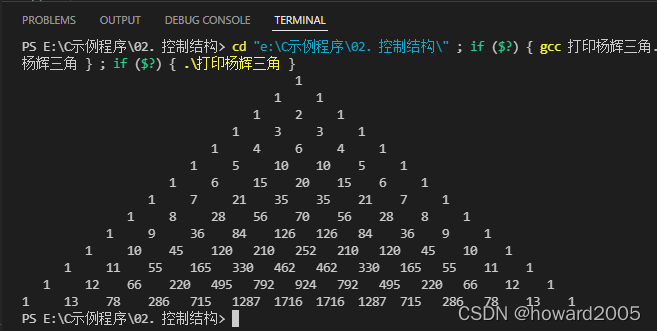
(三)打印乘法九九表
- 作为启蒙教材,我们都背过九九乘法表:一一得一、一二得二、……、九九八十一。而古代是从“九九八十一”开始,因此称“九九表”。九九表的使用,对于完成乘法是大有帮助的。齐桓公纳贤的故事说明,到公元前7世纪时,九九歌诀已不稀罕。也许有人认为这种成绩不值一提。但在古代埃及作乘法却要用倍乘的方式呢。举个例子说明:比如计算23×13,就需要从23开始,加倍得到23×2,23×4,23×8,然后注意到13=1+4+8,于是23+23×4+23×8加起来的结果就是23×13。通过对比,不难看出使用九九表的优越性了。
- 源代码
#include <stdio.h>
int main()
{
int i, j;
for (i = 1; i <= 9; i++)
{
for (j = 1; j <= i; j++)
{
printf("%d×%d=%-2d ", i, j, i * j);
}
printf("\n");
}
}
- 运行结果
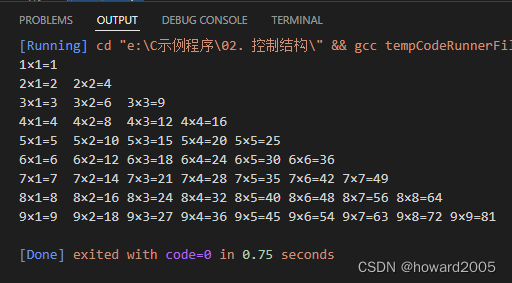
(四)百钱买百鸡问题
-
我国古代数学家张丘建在《算经》一书中曾提出过著名的“百钱买百鸡”问题,该问题叙述如下:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?
-
翻译过来,意思是公鸡一个五块钱,母鸡一个三块钱,小鸡三个一块钱,现在要用一百块钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?
-
需要定义三个整型变量 c o c k cock cock, h e n hen hen, c h i c k chick chick,分别代表公鸡、母鸡和小鸡的购买数量。
有两方面的条件:关于钱的条件与关于鸡的条件
– 钱的条件: c o c k × 5 + h e n × 3 + c h i c k 3 = 100 cock \times5+hen\times3+\displaystyle\frac{chick}{3}=100 cock×5+hen×3+3chick=100
– 鸡的条件: c o c k + h e n + c h i c k = 100 cock+hen+chick=100 cock+hen+chick=100
1、采用三重循环解决百钱买百鸡问题
- 源代码
#include "stdio.h"
int main()
{
int cock, hen, chick, count = 0;
for (cock = 0; cock <= 20; cock++)
{
for (hen = 0; hen <= 34; hen++)
{
for (chick = 0; chick <= 100; chick++)
{
if (cock + hen + chick == 100 &&
cock * 5 + hen * 3 + chick / 3.0 == 100)
{
count++;
printf("cock = %-2d, hen = %-2d, chick = %-2d \n", cock, hen, chick);
}
}
}
}
printf("百钱买百鸡购买方案数:%d\n", count);
}
-
运行结果
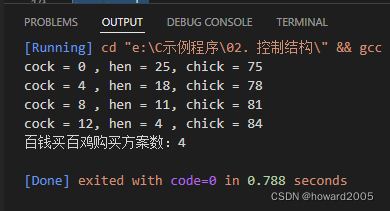
-
验证四种购买方案是否正确
– 方案1: 0 + 25 + 75 = 100 , 0 × 5 + 25 × 3 + 75 3 = 75 + 25 = 100 0+25+75=100, 0\times5+25\times3+\displaystyle\frac{75}{3}=75+25=100 0+25+75=100,0×5+25×3+375=75+25=100
– 方案2: 4 + 18 + 78 = 100 , 4 × 5 + 18 × 3 + 78 3 = 20 + 54 + 26 = 100 4+18+78=100, 4\times5+18\times3+\displaystyle\frac{78}{3}=20+54+26=100 4+18+78=100,4×5+18×3+378=20+54+26=100
– 方案3: 8 + 11 + 81 = 100 , 8 × 5 + 11 × 3 + 81 3 = 40 + 33 + 27 = 100 8+11+81=100, 8\times5+11\times3+\displaystyle\frac{81}{3}=40+33+27=100 8+11+81=100,8×5+11×3+381=40+33+27=100
– 方案4: 12 + 4 + 84 = 100 , 12 × 5 + 4 × 3 + 84 3 = 60 + 12 + 28 = 100 12+4+84=100, 12\times5+4\times3+\displaystyle\frac{84}{3}=60+12+28=100 12+4+84=100,12×5+4×3+384=60+12+28=100 -
注意:有个一个细节问题,条件里用的是
chick / 3.0,而不是chick / 3。在数学上两者没有区别,但是在计算机里就有区别了,因为计算机里不同类型数据存储与运算不一样。 -
采用三重循环固然可以解决百钱买百鸡问题,但是最内层循环里的基本操作次数 = 21 × 35 × 101 = 74 , 235 21\times 35 \times 101=74,235 21×35×101=74,235,时间复杂度就比较高了,我们应该优化解决问题的算法。下面,我们降维处理,采用双重循环来解决此问题。
2、采用双重循环解决百钱买百鸡问题
- 源代码
#include "stdio.h"
int main()
{
int cock, hen, chick, count = 0;
for (cock = 0; cock <= 20; cock++)
{
for (hen = 0; hen <= 34; hen++)
{
chick = 100 - cock - hen;
if (cock * 5 + hen * 3 + chick / 3.0 == 100)
{
count++;
printf("cock = %-2d, hen = %-2d, chick = %-2d \n", cock, hen, chick);
}
}
}
printf("百钱买百鸡购买方案数:%d\n", count);
}
- 运行结果
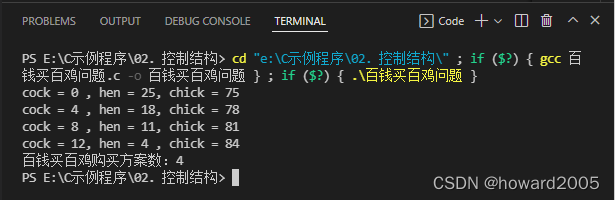
- 采用双重循环解决百钱买百鸡问题,内层循环里的基本操作次数 = 21 × 35 = 735 21\times 35=735 21×35=735,跟三重循环算法相比,时间复杂度就大大降低了,因此双重循环算法是一个更好的算法。
(五)打印水仙花数
1、通过拆分三位整数来实现
- 所谓水仙花数,是指等于其各位数字立方和的三位数。
\qquad
153
=
1
3
+
5
3
+
3
3
153=1^3+5^3+3^3
153=13+53+33
\qquad
370
=
3
3
+
7
3
+
0
3
370=3^3+7^3+0^3
370=33+73+03
\qquad
371
=
3
3
+
7
3
+
1
3
371=3^3+7^3+1^3
371=33+73+13
\qquad
407
=
4
3
+
0
3
+
7
3
407=4^3+0^3+7^3
407=43+03+73
- 分析问题,首先水仙花数是三位数,那么我们可以确定范围:100~999,这个我们可以通过循环结构来搞定:
for (n = 100; n <= 999; n++) {
...
}
-
然后对于这个范围的每个数n,我们要去判断它是否等于其各位数字的立方和,这里的难点或关键在于如何分解一个三位数,得到它的每位数字。
-
假设我们已经把三位数n分解成百位数p3,十位数p2,个位数p1,
这样我们的筛选条件就可以写出来:n == p3 * p3 * p3 + p2 * p2 * p2 + p1 * p1 * p1。 -
如何拆分一个三位数n呢?
-
首先求n的个位数:n % 10
然后要将三位数变成两位数:n = n / 10;
对于新的两位数n,又求它的个位数:n % 10
然后要将两位数变成一位数:n = n / 10; -
也就是说我们可以交替使用求余和整除运算将一个三位数拆分,得到它的个位数、十位数和百位数。当然这个分解方法可以推广到任何多位数的拆分。
-
源代码
#include <stdio.h>
void main()
{
int n;
int p3; // 百位数
int p2; // 十位数
int p1; // 个位数
for (n = 100; n <= 999; n++) // 循环头:初始条件、循环条件、更新条件
{
p1 = n % 10; // 得到个位数
p2 = n / 10 % 10; // 得到十位数
p3 = n / 100; // 得到百位数
if (n == p1 * p1 * p1 + p2 * p2 * p2 + p3 * p3 * p3) // if负责筛选工作
{
printf("%d = %d^3 + %d^3 + %d^3\n", n, p3, p2, p1);
}
}
}
- 运行结果
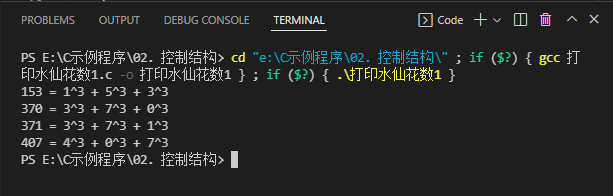
2、通过三重循环筛选三位整数来实现
- 源代码
#include <stdio.h>
void main()
{
int n, i, j, k, count = 0;
for (i = 1; i <= 9; i++) // 百位数[1, 9]
{
for (j = 0; j <= 9; j++) // 十位数[0, 9]
{
for (k = 0; k <= 9; k++) // 个位数[0, 9]
{
n = i * 100 + j * 10 + k;
if (n == i * i * i + j * j * j + k * k * k)
{
count++;
printf("%d = %d^3 + %d^3+ %d^3\n", n, i, j, k);
}
}
}
}
printf("总共有%d个水仙花数。", count);
}
- 运行结果
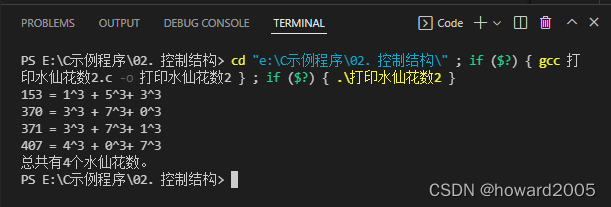
3、通过整数转换成字符串来实现
- iota()函数:
char *itoa( int value, char *string,int radix);
value:欲转换的数据
string:目标字符串的地址
radix:转换后的进制数,可以是10进制、16进制等,范围必须在 2~36
#include <stdio.h>
#include <stdlib.h>
void main()
{
int n;
int p3; // 百位数
int p2; // 十位数
int p1; // 个位数
char p[3] = {0};
for (n = 100; n <= 999; n++)
{
itoa(n, p, 10); // 10表示十进制
p3 = (int)p[0] - 48;
p2 = (int)p[1] - 48;
p1 = (int)p[2] - 48;
if (n == p3 * p3 * p3 + p2 * p2 * p2 + p1 * p1 * p1)
{
printf("%d = %d^3 + %d^3 + %d^3\n", n, p3, p2, p1);
}
}
}
-
说明:字符
0的ASCII码是48,因此要把字符0变成数字0,需要减去48 -
运行结果
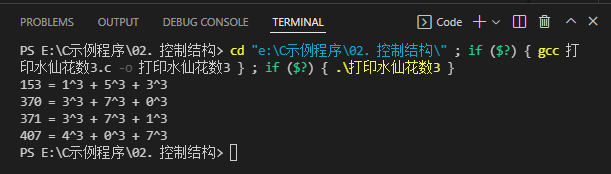
(六)验证四平方和定理
- 四平方和定理,又称为拉格朗日定理:每个正整数都可以表示为至多4个正整数的平方和。如果把0包括进去,就正好可以表示为4个数的平方和。比如: 5 = 0 2 + 0 2 + 1 2 + 2 2 5 = 0^2 + 0^2 + 1^2 + 2^2 5=02+02+12+22, 7 = 1 2 + 1 2 + 1 2 + 2 2 7 = 1^2 + 1^2 + 1^2 + 2^2 7=12+12+12+22
- 对于一个给定的正整数,可能存在多种平方和的表示法。要求你对4个数排序: 0 ≤ a ≤ b ≤ c ≤ d 0\le a \le b \le c \le d 0≤a≤b≤c≤d,并对所有的可能表示法按 a , b , c , d a,b,c,d a,b,c,d 为联合主键升序排列,最后输出第一个表示法。程序输入为一个正整数 N ( N < 5000000 ) N (N<5000000) N(N<5000000),要求输出 4 4 4个非负整数,按从小到大排序,中间用空格分开。
- 例如,输入: 5 5 5,则程序应该输出: 0 0 1 2 0\ 0\ 1\ 2 0 0 1 2
- 源代码
#include <stdio.h>
#include <math.h>
int main()
{
int n, a, b, c, d, m;
printf("n = ");
scanf("%d", &n);
for (a = 0; a <= sqrt(n); a++)
{
for (b = a; b <= sqrt(n); b++)
{
for (c = b; c <= sqrt(n); c++)
{
m = n - a * a - b * b - c * c;
if (sqrt(m) == (int)sqrt(m))
{
d = (int)sqrt(m);
printf("%d %d %d %d\n", a, b, c, d);
return 0;
}
}
}
}
return 0;
}
- 运行结果
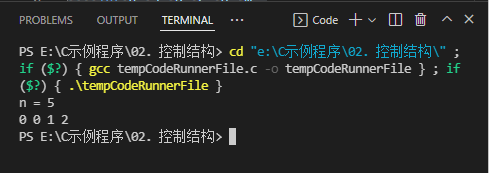
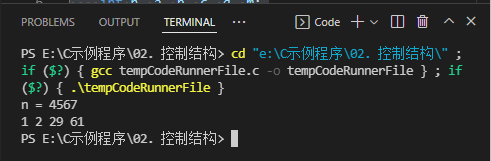
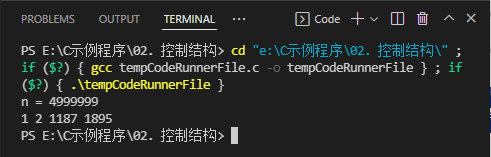
(七)指定范围有多少纯质数
- 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。如果一个正整数只有 1 和它本身两个约数,则称为一个质数(又称素数)。前几个质数: 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , … 2,3,5,7,11,13,17,19,23,29,31,37,… 2,3,5,7,11,13,17,19,23,29,31,37,…。如果一个质数的所有十进制数位都是质数,我们称它为纯质数。例如: 2 , 3 , 5 , 7 , 23 , 37 2,3,5,7,23,37 2,3,5,7,23,37都是纯质数,而 11 , 13 , 17 , 19 , 29 , 31 11, 13, 17, 19, 29, 31 11,13,17,19,29,31不是纯质数。当然 1 , 4 , 35 1, 4, 35 1,4,35也不是纯质数。请问,在 1 到 20210605 中,有多少个纯质数?
- 源代码
#include <stdio.h>
#include <math.h>
// 判断n是不是质数
int isPrimeNumber(int n)
{
int i;
for (i = 2; i <= sqrt(n); i++)
if (n % i == 0)
return 0;
if (n == 1)
return 0;
return 1;
}
// 判断k每位数字是否是质数
int isPrimeByDigit(int k)
{
while (k > 0)
{
int m = k % 10;
if (m == 0 || m == 1 || m == 4 || m == 6 || m == 8 || m == 9)
{
return 0;
}
k = k / 10;
}
return 1;
}
void main()
{
int n, k, count = 0;
for (n = 1; n <= 20210605; n++)
{
if (isPrimeNumber(n) && isPrimeByDigit(n))
count++;
}
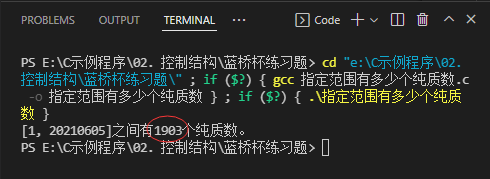
printf("[1, 20210605]之间有%d个纯质数。\n", count);
}
- 运行结果
(八)输出10000以内的完全数
- 完全数是等于真因子之和的数
- 源代码
#include <stdio.h>
int sum_of_factors(int n)
{
int i, sum = 0;
for (i = 1; i <= n / 2; i++)
if (n % i == 0)
sum = sum + i;
return sum;
}
void main()
{
int i, n;
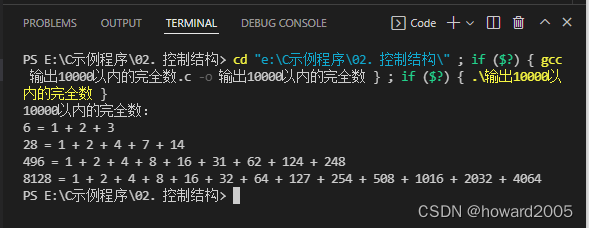
printf("10000以内的完全数:\n");
for (n = 1; n <= 10000; n++)
{
if (n == sum_of_factors(n))
{
printf("%d = 1", n);
for (i = 2; i <= n / 2; i++)
if (n % i == 0)
printf(" + %d", i);
printf("\n");
}
}
}
- 运行结果
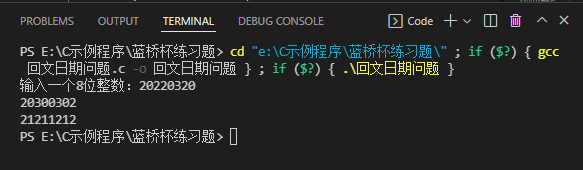
(九)输出指定要求的回文日期
- 2020 年春节期间,有一个特殊的日期引起了大家的注意:2020 年 2 月 2 日。因为如果将这个日期按“
yyyymmdd”的格式写成一个 8 位数是 20200202,恰好是一个回文数。我们称这样的日期是回文日期。有人表示 20200202 是“千年一遇”的特殊日子。对此小明很不认同,因为不到 2 年之后就是下一个回文日期:20211202 即 2021年 12月2日。也有人表示 20200202 并不仅仅是一个回文日期,还是一个 ABABBABA 型的回文日期。对此小明也不认同,因为大约 100 年后就能遇到下一个 ABABBABA 型的回文日期:21211212即2121 年 12 月 12 日。算不上“千年一遇”,顶多算“千年两遇”。 - 给定一个 8 位数的日期,请你计算该日期之后下一个回文日期和下一个 ABABBABA 型的回文日期各是哪一天。
- 输入描述:输入包含一个八位整数 N,表示日期。
对于所有评测用例,10000101 ≤ N ≤ 89991231,保证 N 是一个合法日期的 8 位数 - 输出描述:输出两行,每行 1 个八位数。第一行表示下一个回文日期,第二行表示下一个 ABABBABA 型
的回文日期。 - 源代码
#include <stdio.h>
#include <stdlib.h>
// 判断日期是否合法
int isLegalDate(int n)
{
char strDate[8];
int k, year, month, day;
k = n;
itoa(k, strDate, 10); // 调用此函数会改变第一个参数值,所以传入与n值相同的k,免得修改了参数n
// 年份要求(题目要求)
year = ((int)strDate[0] - 48) * 1000 + ((int)strDate[1] - 48) * 100 + ((int)strDate[2] - 48) * 10 + ((int)strDate[3] - 48);
if (year < 1000 || year > 8999)
return 0;
// 月份要求
month = ((int)strDate[4] - 48) * 10 + ((int)strDate[5] - 48);
if (month < 1 || month > 12)
return 0;
// 天日要求
day = ((int)strDate[6] - 48) * 10 + ((int)strDate[7] - 48);
if (month == 1 || month == 3 || month == 5 || month == 7 || month == 8 || month == 10 || month == 12)
{
if (day < 1 || day > 31)
return 0;
}
if (month == 4 || month == 6 || month == 9 || month == 11)
{
if (day < 1 || day > 30)
return 0;
}
if (month == 2)
{
if (year % 4 == 0 && year % 100 != 0 || year % 400 == 0)
{
if (day < 1 || day > 29)
return 0;
}
else
{
if (day < 1 || day > 28)
return 0;
}
}
return 1;
}
// 判断是否是回文日期
int isPalindromicDate(int n)
{
int i, k;
char strDate[8];
k = n;
itoa(k, strDate, 10); // 调用此函数会改变第一个参数值,所以传入与n值相同的k,免得修改了参数n
if (!isLegalDate(n))
return 0;
for (i = 0; i < 8; i++)
{
if (strDate[i] != strDate[8 - i - 1])
return 0;
}
return 1;
}
// 判断是否是ABABBABA型回文日期
int isABABBABA(int n)
{
int i, k, m;
char strDate[8];
k = n;
itoa(k, strDate, 10); // 调用此函数会改变第一个参数值,所以传入与n值相同的k,免得修改了参数n
if (isPalindromicDate(n))
{
if (strDate[0] == strDate[2] && strDate[1] == strDate[3])
return 1;
}
return 0;
}
void main()
{
int n, m, k;
char strDate[8];
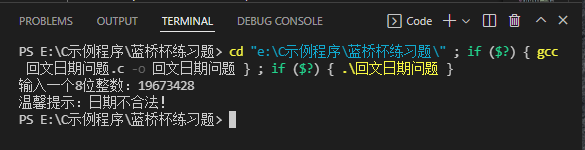
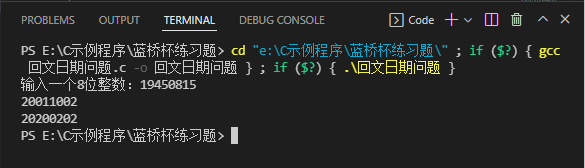
printf("输入一个8位整数:");
scanf("%d", &n);
if (isLegalDate(n))
{
// 输出下一个回文日期
for (m = n + 1; m <= 89991231; m++)
{
if (isPalindromicDate(m))
{
printf("%d\n", m);
break;
}
}
// 输出下一个ABABBABA型回文日期
for (k = m + 1; k <= 89991231; k++)
{
if (isABABBABA(k))
{
printf("%d\n", k);
break;
}
}
}
else
{
printf("温馨提示:日期不合法!");
}
}
- 运行结果
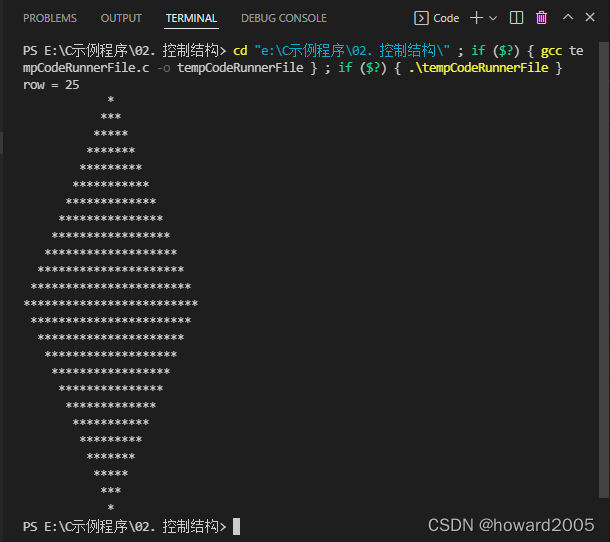
(十)打印实心钻石
- 实心钻石,其实由一个正立的等腰三角形和一个倒立的等腰三角形组合而成,也就是一个菱形。
- 源代码
#include <stdio.h>
#include <stdlib.h>
void main()
{
int row, half, i, j;
// 输入行数
printf("row = ");
scanf("%d", &row);
// 打印钻石上半部分
half = row / 2 + 1;
for (i = 1; i <= half; i++)
{
// 打印前导空格
for (j = 1; j <= half - i; j++)
{
printf(" ");
}
// 打印星号
for (j = 1; j <= 2 * i - 1; j++)
{
printf("*");
}
// 换行
printf("\n");
}
// 打印钻石下半部分
for (i = 1; i < half; i++)
{
// 打印前导空格
for (j = 1; j <= i; j++)
{
printf(" ");
}
// 打印星号
for (j = 1; j <= 2 * (half - i - 1) + 1; j++)
{
printf("*");
}
// 换行
printf("\n");
}
}
- 运行结果
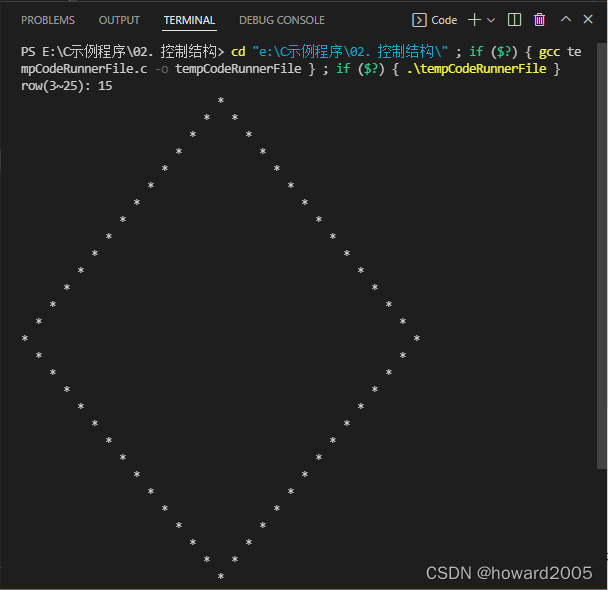
(十一)打印空心钻石
- 源代码
#include <stdio.h>
void main() {
int i, j, row, col;
char c[25][50];
printf("row(3~25): ");
scanf("%d", &row);
if (row < 3 || row > 25) {
printf("超出范围!");
return;
}
col = 2 * row;
for(i = 0; i < row; i++) {
for(j = 0; j < col; j++) {
c[i][j] = ' ';
}
}
for(i = 0; i < row; i++) {
j = row - 1 - i;
c[i][j] = '*';
j = j + 2 * i;
c[i][j] = '*';
}
for(i = 0; i < row; i++) {
for(j = 0; j < col; j++) {
printf("%c ", c[i][j]);
}
printf("\n");
}
for(i = 0; i < row - 1; i++) {
for(j = 0; j < col; j++) {
c[i][j] = ' ';
}
}
for(i = 0; i < row - 1; i++) {
j = i + 1;
c[i][j] = '*';
j = col - i - 3;
c[i][j] = '*';
}
for(i = 0; i < row - 1; i++) {
for(j = 0; j < col; j++) {
printf("%c ", c[i][j]);
}
printf("\n");
}
}
- 运行结果
(十二)验证哥德巴赫猜想
- 哥德巴赫1742年在给欧拉的信中提出了以下猜想:任一大于2的整数都可写成三个质数之和,但是哥德巴赫自己无法证明它,于是就写信请教赫赫有名的大数学家欧拉帮忙证明,但是一直到死,欧拉也无法证明。因现今数学界已经不使用“1也是素数”这个约定,原初猜想的现代陈述为:任一大于5的整数都可写成三个质数之和。(n>5:当n为偶数,n=2+(n-2),n-2也是偶数,可以分解为两个质数的和;当n为奇数,n=3+(n-3),n-3也是偶数,可以分解为两个质数的和)欧拉在回信中也提出另一等价版本,即任一大于2的偶数都可写成两个质数之和。今日常见的猜想陈述为欧拉的版本。把命题"任一充分大的偶数都可以表示成为一个素因子个数不超过a个的数与另一个素因子不超过b个的数之和记作“a+b”。1966年陈景润证明了“1+2”成立,即“任一充分大的偶数都可以表示成二个素数的和,或是一个素数和一个半素数的和”。
- 今日常见的猜想陈述为欧拉的版本,即任一大于2的偶数都可写成两个素数之和,亦称为“强哥德巴赫猜想”或“关于偶数的哥德巴赫猜想”。
- 从关于偶数的哥德巴赫猜想,可推出:任何一个大于7的奇数都能被表示成三个奇质数的和。后者称为“弱哥德巴赫猜想”或“关于奇数的哥德巴赫猜想”。若关于偶数的哥德巴赫猜想是对的,则关于奇数的哥德巴赫猜想也会是对的。2013年5月,巴黎高等师范学院研究员哈洛德·贺欧夫各特发表了两篇论文,宣布彻底证明了弱哥德巴赫猜想。
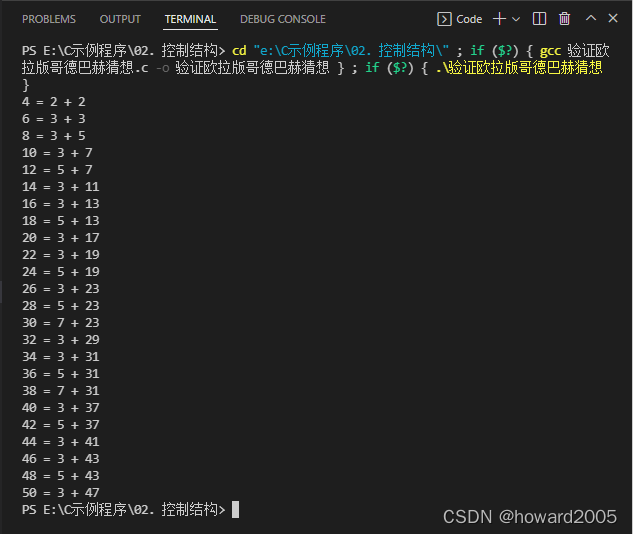
1、欧拉版哥德巴赫猜想
- 任一大于2的偶数都可写成两个素数之和
- 源代码
#include <stdio.h>
#include <math.h>
int isPrimeNumber(int n)
{
int i, flag = 1;
for (i = 2; i <= sqrt(n); i++)
{
if (n % i == 0)
{
flag = 0;
break;
}
}
if (n == 1)
flag = 0;
return flag;
}
void main()
{
int i, n;
for (n = 4; n <= 100; n = n + 2)
{
for (i = 2; i <= n / 2; i++)
{
if (isPrimeNumber(i) && isPrimeNumber(n - i))
{
printf("%d = %d + %d\n", n, i, n - i);
break;
}
}
}
}
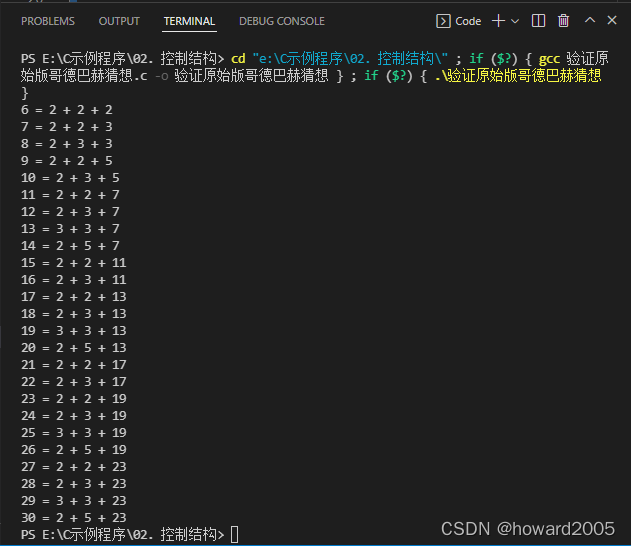
- 运行结果
2、原始版哥德巴赫猜想
- 任一大于5的整数都可写成三个质数之和
- 源代码
#include <stdio.h>
#include <math.h>
int isPrimeNumber(int n)
{
int i, flag = 1;
for (i = 2; i <= sqrt(n); i++)
{
if (n % i == 0)
{
flag = 0;
break;
}
}
if (n == 1)
flag = 0;
return flag;
}
void main()
{
int i, j, n, p1, p2, p3;
for (n = 5; n <= 30; n++)
{
for (i = 2; i <= n / 2; i++)
{
if (isPrimeNumber(i))
{
p1 = i;
for (j = i; j <= (n - p1) / 2; j++)
{
if (isPrimeNumber(j))
{
p2 = j;
p3 = n - p1 - p2;
if (isPrimeNumber(p3) && p3 >= p2)
{
printf("%d = %d + %d + %d\n", n, p1, p2, p3);
goto next;
}
}
}
}
}
next:
printf("");
}
}
- 运行结果
二、使用指针
- 指针:在计算机内存里有很多存储单元(以字节为单位),为了便于存取数据,给每一个存储单元编号,这个编号就叫做地址(address)。在C语言里,变量的地址也叫做指针。
- 指针变量:专门用来存放指针的变量。如果指针是指向整型数据,那么存放该指针的变量也必须是整型的,也就是类型要保持一致。有了指针变量之后,我们访问数据就多了一种方式:间接访问方式。
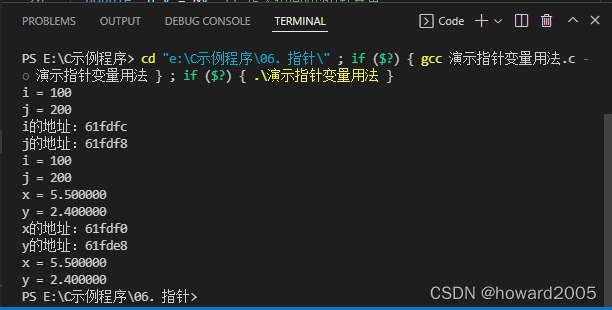
(一)演示指针变量用法
- 源代码
#include "stdio.h"
int main()
{
// 声明部分
int i = 100;
int j = 200;
double x = 5.5;
double y = 2.4;
/*
&——取址运算符
*——取值运算符
它们是互逆运算
*/
int *p_i = &i; // 定义指向i的指针变量
int *p_j = &j; // 定义指向j的指针变量
double *p_x = &x; // 定义指向x的指针变量
double *p_y = &y; // 定义指向y的指针变量
// 输出部分
printf("i = %d\n", i); // 通过变量名直接访问数据
printf("j = %d\n", j); // 通过变量名直接访问数据
printf("i的地址:%x\n", p_i); // 输出指针变量p_i的值,即i的地址
printf("j的地址:%x\n", p_j); // 输出指针变量p_j的值,即j的地址
printf("i = %d\n", *p_i); // 通过指针变量间接访问数据
printf("j = %d\n", *p_j); // 通过指针变量间接访问数据
printf("x = %f\n", x); // 通过变量名直接访问数据
printf("y = %f\n", y); // 通过变量名直接访问数据
printf("x的地址:%x\n", p_x); // 输出指针变量p_x的值,即x的地址
printf("y的地址:%x\n", p_y); // 输出指针变量p_y的值,即y的地址
printf("x = %f\n", *p_x); // 通过指针变量间接访问数据
printf("y = %f\n", *p_y); // 通过指针变量间接访问数据
return 0;
}
- 运行结果
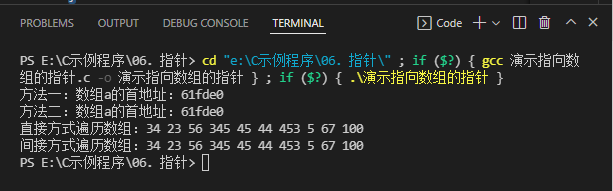
(二)演示指向数组的指针
-
指针可以指向简单变量、数组、函数、结构体和文件,这里我们只讲述指向数组的指针,其中会涉及到指针的运算。为了简单起见,我们拿整型数组来说明指向数组的指针。
-
首先,我们定义一个整型数组:int a[10]; 因为数组在计算机内存里是连续存放的,所以只要我们知道第一个元素的地址,那么我们可以推算出数组其它元素的地址。首地址:
&a[0],其实,数组名a的值就是数组的首地址&a[0]。 -
现在有一个任务,我们要遍历整个一维数组,当然可以用以前的方法,通过for循环与下表访问元素来访问每一个数组元素,这是直接遍历数组的方式。但现在我们要用一种新方法来完成这个任务。通过指向数组的指针来实现。
int *p_a;
p_a = a;
p_a = &a[0];
-
两句赋值语句效果完全一样,把数组首地址保存到指针变量
p_a里。 -
p_a —— 第一个元素的地址
-
p_a + 1 —— 第二个元素的地址
-
……
-
p_a + 9 —— 最后一个元素的地址
-
有了每个数组元素的地址,怎么访问它的数据,很简单,利用*(取值运算符)就可以得到该地址存放的数据,这是一种间接访问数据的方式。
-
*p_a —— 第一个元素的值
-
*(p_a + 1) —— 第二个元素的值
-
……
-
*(p_a + 9) —— 最后一个元素的值
-
这样我们可以通过指针运算来间接地遍历数组。
-
源代码
#include "stdio.h"
int main()
{
// 声明部分
int i;
int a[10] = {34, 23, 56, 345, 45, 44, 453, 5, 67, 100};
int *p_a = a; // 定义指向数组的指针变量
// 输出数组的首地址,也就是第一个元素的地址
// 方法一:&a[0]
printf("方法一:数组a的首地址:%x\n", &a[0]);
// 方法二:a
printf("方法二:数组a的首地址:%x\n", a);
// 通过下标变量直接遍历数组
printf("直接方式遍历数组:");
for (i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 通过指针变量间接遍历数组
printf("间接方式遍历数组:");
for (i = 0; i < 10; i++)
{
printf("%d ", *(p_a + i));
}
return 0;
}
- 运行结果
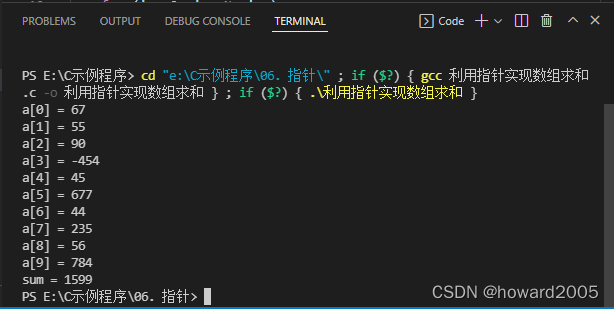
(三)利用指针实现数组求和
- 源代码
#include "stdio.h"
#define N 10
void main()
{
//声明部分
int i, a[N], sum = 0, *p;
//输入部分
p = a;
for (i = 0; i < N; i++)
{
printf("a[%d] = ", i);
scanf("%d", (p + i));
}
//处理部分
p = a;
for (i = 0; i < N; i++)
{
sum = sum + *(p + i);
}
// 输出部分
printf("sum = %d\n", sum);
}
- 运行结果
(四)实现字符串与数字加密
(1)编写fun()函数,该函数的功能是将字符串中字符和数字进行加密。如果是字母,转换成其后第三个,如字母A转换成D,字母X转换成A;如果是数字,转换为其前第二个,如数字3转换成1,数字1转换为9;其余字符保持不变。
(2)编写main()函数,输入一个字符串,并把转换后的字符串输出。
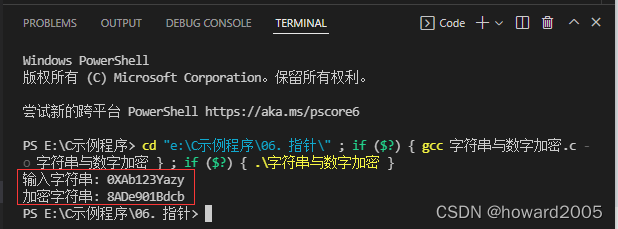
如输入0XAb123Yazy,则程序运行结果如下所示:
输入字符串:0XAb123Yazy
加密字符串:8ADe901Bdcb
- 源代码
#include "stdio.h"
#include "string.h"
#include <stdlib.h>
char *fun(char *s);
void main()
{
char *s = (char *)malloc(sizeof(char) * 100);
printf("输入字符串: ");
scanf("%s", s);
printf("加密字符串: %s", fun(s));
}
char *fun(char *s)
{
int i, len = strlen(s);
for (i = 0; i < len; i++)
{
char c = s[i];
if (c >= 'A' && c <= 'W')
{
c = c + 3;
}
else if (c >= 'X' && c <= 'Z')
{
c = c - 23;
}
else if (c >= 'a' && c <= 'w')
{
c = c + 3;
}
else if (c >= 'x' && c <= 'z')
{
c = c - 23;
}
else if (c >= '2' && c <= '9')
{
c = c - 2;
}
else if (c >= '0' && c <= '1')
{
c = c + 8;
}
s[i] = c;
}
return s;
}
- 运行结果
三、了解结构体
- “结构体类型”是由不同数据类型变量组成的集合体,相当于其它高级语言中的记录。结构体类型的数据由若干称为“成员”的数据组成,每个成员既可以是一个基本数据类型的数据,也可以是另一个构造类型的数据。
- 结构体定义
struct 类型名 {
类型1 成员名1;
类型2 成员名2;
……
};
-
以上整个部分是一个数据类型,与整型的
int是同样地位。可用typedef把结构体类型替换成一个只有几个字母的简短标识符。 -
结构体变量的声明:结构体变量是用说明的结构体类型所定义的一个变量,与结构体类型不是一回事。一个结构体变量所占字节数为其所有成员所占字节数之和。如struct Student {char name[10]; int age;} a, b; 则表明定义了两个结构体变量a,b,每个变量占14个字节。a,b与int i, j; 中的变量i,j是同样地位。
-
结构体成员的引用
–(1)结构体变量名.成员名
–(2)指针变量名->成员名
–(3)(*指针变量名).成员名 -
点
.称为成员运算符,箭头->称为结构指向运算符
(一)显示学生记录
- 源代码
#include <stdio.h>
#include <string.h>
// 定义结构体
struct Student
{
int num;
char name[20];
char sex[4];
int age;
double score;
char address[30];
};
void main()
{
struct Student stu1, stu2, stu3; // 声明结构体变量
// 给第一个学生赋值
stu1.num = 1;
strcpy(stu1.name, "李平");
strcpy(stu1.sex, "男");
stu1.age = 18;
stu1.score = 98.5;
strcpy(stu1.address, "泸州江阳区瓦窑坝西35#");
// 给第二个学生赋值
stu2.num = 2;
strcpy(stu2.name, "王红");
strcpy(stu2.sex, "女");
stu2.age = 19;
stu2.score = 99.5;
strcpy(stu2.address, "泸州龙马潭区潇湘路15#");
// 给第三个学生赋值
stu3.num = 3;
strcpy(stu3.name, "张枫");
strcpy(stu3.sex, "男");
stu3.age = 21;
stu3.score = 69.0;
strcpy(stu3.address, "泸州龙马潭区潇湘路15#");
//输出三个学生的信息
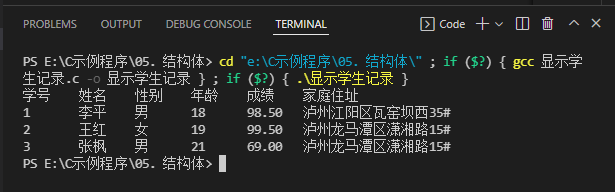
printf("学号\t姓名\t性别\t年龄\t成绩\t家庭住址\n");
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", stu1.num, stu1.name, stu1.sex, stu1.age, stu1.score, stu1.address);
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", stu2.num, stu2.name, stu2.sex, stu2.age, stu2.score, stu2.address);
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", stu3.num, stu3.name, stu3.sex, stu3.age, stu3.score, stu3.address);
}
- 运行结果
(二)使用指针指向结构体
- 源代码
#include <stdio.h>
#include <string.h>
// 定义结构体
struct Student
{
int num;
char name[20];
char sex[4];
int age;
double score;
char address[30];
};
void main()
{
struct Student stu1, stu2, stu3; // 声明结构体变量
struct Student *s1, *s2, *s3; // 声明结构体指针
s1 = &stu1;
s2 = &stu2;
s3 = &stu3;
// 给第一个学生赋值
s1->num = 1;
strcpy(s1->name, "李平");
strcpy(s1->sex, "男");
s1->age = 18;
s1->score = 98.5;
strcpy(s1->address, "泸州江阳区瓦窑坝 35#");
// 给第二个学生赋值
s2->num = 2;
strcpy(s2->name, "王红");
strcpy(s2->sex, "女");
s2->age = 19;
s2->score = 99.5;
strcpy(s2->address, "泸州龙马潭区潇湘路15#");
// 给第三个学生赋值
s3->num = 3;
strcpy(s3->name, "张枫");
strcpy(s3->sex, "男");
s3->age = 21;
s3->score = 69.0;
strcpy(s3->address, "泸州龙马潭区潇湘路15#");
// 输出三个学生的信息
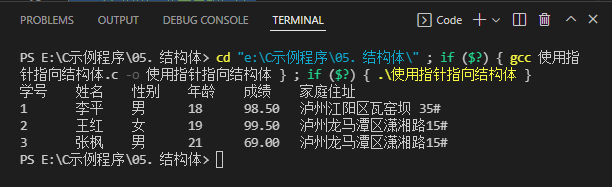
printf("学号\t姓名\t性别\t年龄\t成绩\t家庭住址\n");
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", s1->num, s1->name, s1->sex, s1->age, s1->score, s1->address);
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", s2->num, s2->name, s2->sex, s2->age, s2->score, s2->address);
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", s3->num, s3->name, s3->sex, s3->age, s3->score, s3->address);
}
- 运行结果
- 输出三个学生信息,代码还可以这样写。
printf("学号\t姓名\t性别\t年龄\t成绩\t家庭住址\n");
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", (*s1).num, (*s1).name, (*s1).sex, (*s1).age, (*s1).score, (*s1).address);
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", (*s2).num, (*s2).name, (*s2).sex, (*s2).age, (*s2).score, (*s2).address);
printf("%d\t%s\t%s\t%d\t%.2f\t%s\n", (*s3).num, (*s3).name, (*s3).sex, (*s3).age, (*s3).score, (*s3).address);
四、文件操作
- 文件在进行读写操作之前要先打开,使用完毕要关闭。所谓打开文件,实际上是建立文件的各种有关信息,并使文件指针指向该文件,以便进行其它操作。关闭文件则断开指针与文件之间的联系,也就禁止再对该文件进行操作。在C语言中,文件操作都是由库函数来完成的。
- 文件打开函数 - fopen():
文件指针名 = fopen(文件名, 文件使用方式); - 文件使用方式
- “rt”只读打开一个文本文件,只允许读数据
- “wt”只写打开或建立一个文本文件,只允许写数据
- “at”追加打开一个文本文件,并在文件末尾写数据
- “rb”只读打开一个二进制文件,只允许读数据
- “wb”只写打开或建立一个二进制文件,只允许写数据
- “ab”追加打开一个二进制文件,并在文件末尾写数据
- “rt+”读写打开一个文本文件,允许读和写
- “wt+”读写打开或建立一个文本文件,允许读写
- “at+”读写打开一个文本文件,允许读,或在文件末追加数据
- “rb+”读写打开一个二进制文件,允许读和写
- “wb+”读写打开或建立一个二进制文件,允许读和写
- “ab+”读写打开一个二进制文件,允许读,或在文件末追加数据
- 在打开一个文件时,如果出错,
fopen将返回一个空指针值NULL。在程序中可以用这一信息来判别是否完成打开文件的工作,并作相应的处理。 - 文件关闭函数 - fclose():
fclose(文件指针名);“文件指针名”必须是被说明为FILE类型的指针变量。 - 文件读写函数
字符读写函数 :fgetc()和fputc()
字符串读写函数:fgets()和fputs()
数据块读写函数:fread()和fwrite()
格式化读写函数:fscanf()和fprintf()
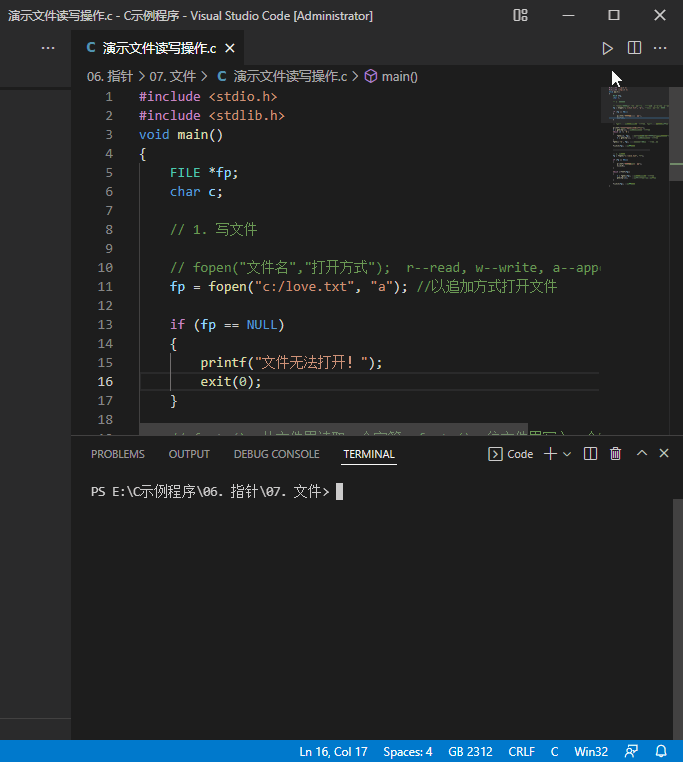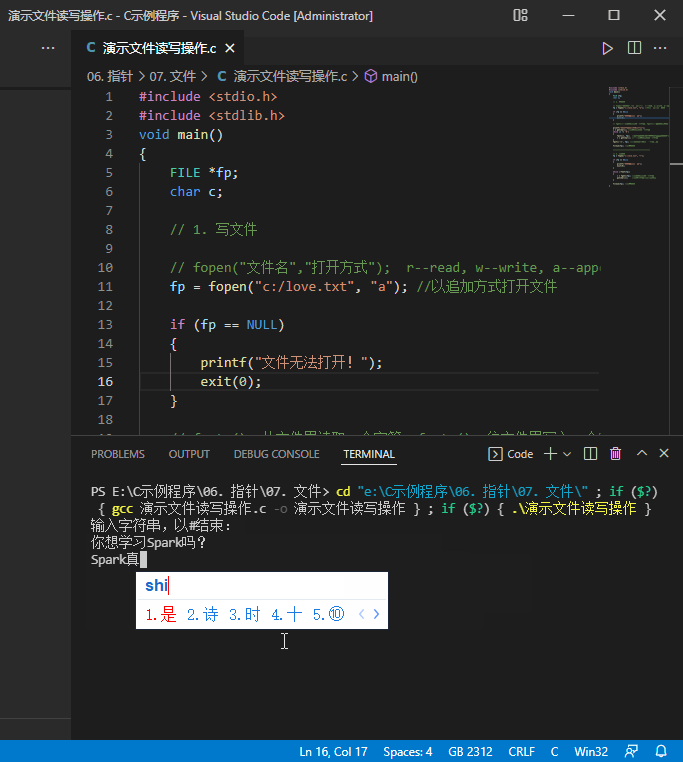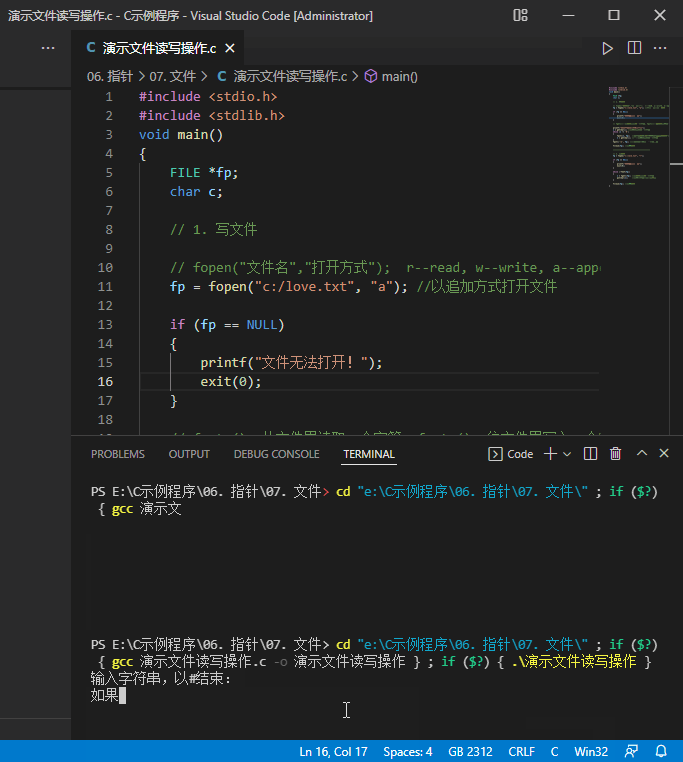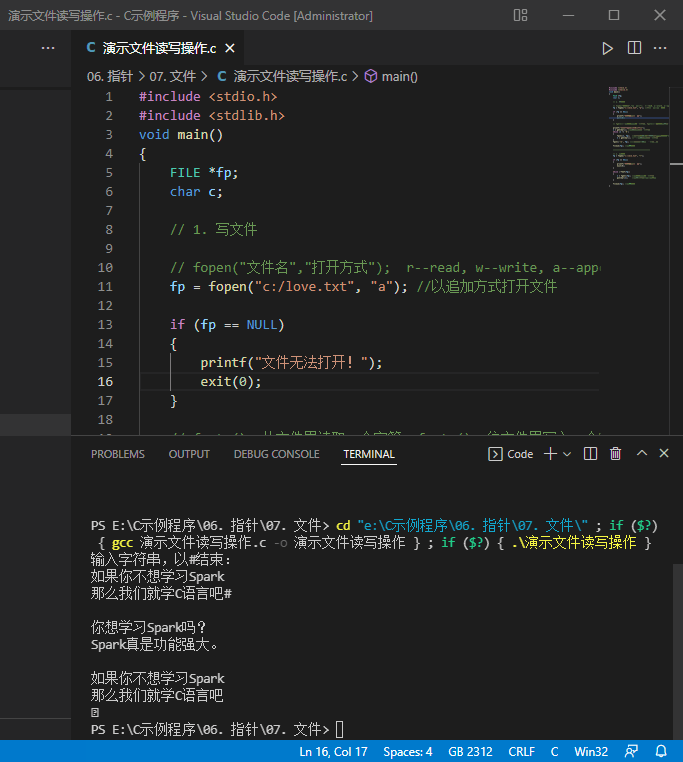
(一)演示文件读写操作
- 源代码
#include <stdio.h>
#include <stdlib.h>
void main()
{
FILE *fp;
char c;
// 1. 写文件
// fopen("文件名","打开方式"); r--read, w--write, a--append
fp = fopen("c:/love.txt", "a"); //以追加方式打开文件
if (fp == NULL)
{
printf("文件无法打开!");
exit(0);
}
// fgetc()--从文件里读取一个字符, fputc()--往文件里写入一个字符
printf("输入字符串,以#结束:");
c = getchar(); //从键盘上输入一个字符
while (c != '#')
{
fputc(c, fp); //将字符变量c的内容写入fp指向的文件"c:\love.txt"
c = getchar(); //继续从键盘上输入一个字符
}
fputc('\n', fp); //每次输入完之后加一个换行符
fclose(fp); //关闭文件
/////////////////////////////////////
// 2. 读文件
fp = fopen("c:/love.txt", "r");
if (fp == NULL)
{
printf("文件无法打开!");
exit(0);
}
while (!feof(fp))
{
c = fgetc(fp); //从文件里读取一个字符
putchar(c); //把这个字符显示在屏幕上
}
fclose(fp); //关闭文件
}
- 运行结果
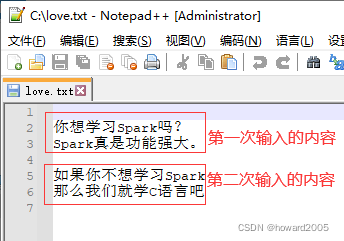
- 说明:因为写文件采用的是追加方式,所以文件
c:\love.txt里最后会有两次次输入的内容。
(二)实现文件复制功能
- 将
C:\Windows\win.ini文件复制到D盘根目录,改名为win.txt同时在控制台输出该文件内容。 - 源代码
#include <stdio.h>
#include <stdlib.h>
void main()
{
FILE *fp1; // 源文件
FILE *fp2; // 目标文件
char c;
fp1 = fopen("C:/Windows/win.ini", "r");
fp2 = fopen("D:/win.txt", "w");
// 遍历源文件
while (!feof(fp1))
{
c = fgetc(fp1); //从源文件文件里读取一个字符
putchar(c); //把这个字符显示在屏幕上
fputc(c, fp2); // 将这个字符写入目标文件
}
// 关闭文件
fclose(fp1);
fclose(fp2);
}
- 运行结果
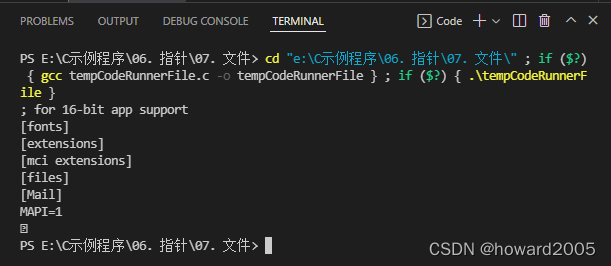
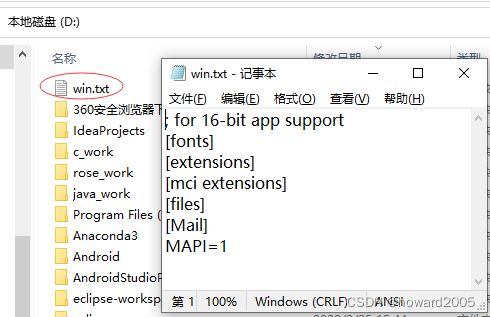
- 查看生成的目标文件
D:\win.txt








 本文详细介绍了编程中的各种算法,包括控制结构、指针运用、结构体理解以及文件操作。从斐波那契数列到杨辉三角形,再到乘法九九表和水仙花数,深入浅出地展示了算法的实际应用。同时,文章探讨了百钱买百鸡问题的解决方案,以及如何验证四平方和定理。此外,还讲解了如何通过指针访问数组和结构体,以及实现了文件的读写操作。
本文详细介绍了编程中的各种算法,包括控制结构、指针运用、结构体理解以及文件操作。从斐波那契数列到杨辉三角形,再到乘法九九表和水仙花数,深入浅出地展示了算法的实际应用。同时,文章探讨了百钱买百鸡问题的解决方案,以及如何验证四平方和定理。此外,还讲解了如何通过指针访问数组和结构体,以及实现了文件的读写操作。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










