本文详细介绍了矩阵的各种运算，包括算术运算如加减乘除、乘方、左除以及矩阵乘法、点乘和点除。通过实例演示了如何使用这些运算解决线性方程组，并给出了具体步骤和解题结果。
一、算术运算
（一）算术运算符
| 运算符 | 定义 |
|---|---|
| + | 算术加 |
| - | 算术减 |
| * | 算术乘 |
| .* | 点乘 |
| ^ | 算术乘方 |
| .^ | 点乘方 |
| \ | 算术左除 |
| .\ | 点左除 |
| / | 算术右除 |
| ./ | 点右除 |
' | 矩阵转置。当矩阵是复数时，求矩阵的共轭转置 |
.' | 矩阵转置。当矩阵是复数时，不求矩阵的共轭转置 |
（二）案例演示
1、算术加减乘运算
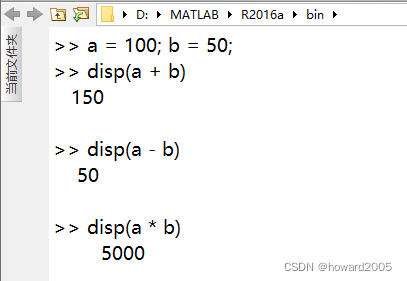
2、算术除运算
3、乘方运算
（1）算术乘方运算
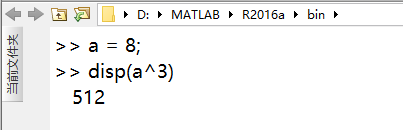
（2）矩阵点乘方运算
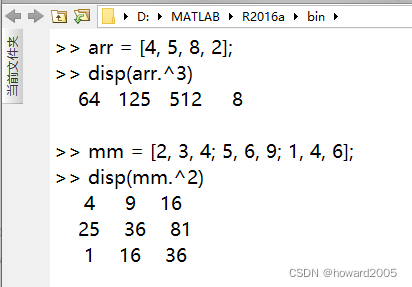
4、矩阵左除运算
- 求解线性方程组： { x + 2 y + 3 z = 14 ( 1 ) 2 x − 4 y + z = − 3 ( 2 ) 3 x + 5 y − 2 z = 7 ( 3 ) \begin{cases} x + 2y + 3z = 14 &(1)\\ 2x -4y +z = -3 &(2)\\ 3x + 5y - 2z = 7 &(3) \end{cases} ⎩⎪⎨⎪⎧x+2y+3z=142x−4y+z=−33x+5y−2z=7(1)(2)(3)
A = [ 1 2 3 2 − 4 1 3 5 − 2 ] A=\left[ \begin{matrix} 1 & 2 & 3 \\ 2 & -4 & 1\\ 3 & 5 & -2 \\ \end{matrix} \right] A=⎣⎡1232−4531−2⎦⎤， B = [ 14 − 3 7 ] B=\left[ \begin{matrix} 14 \\ -3\\ 7 \\ \end{matrix} \right] B=⎣⎡14−37⎦⎤， X = [ x y z ] X=\left[ \begin{matrix} x \\ y\\ z \\ \end{matrix} \right] X=⎣⎡xyz⎦⎤
- 线性方程组表示为 A X = B AX=B AX=B，即- [ 1 2 3 2 − 4 1 3 5 − 2 ] \left[ \begin{matrix} 1 & 2 & 3 \\ 2 & -4 & 1\\ 3 & 5 & -2 \\ \end{matrix} \right] ⎣⎡1232−4531−2⎦⎤ [ x y z ] \left[ \begin{matrix} x \\ y\\ z \\ \end{matrix} \right] ⎣⎡xyz⎦⎤ = [ 14 − 3 7 ] =\left[ \begin{matrix} 14 \\ -3\\ 7 \\ \end{matrix} \right] =⎣⎡14−37⎦⎤
-
X
=
A
−
1
B
X=A^{-1}B
X=A−1B相当于
X
=
B
÷
A
X=B\div A
X=B÷A，是左除
- 所以方程组的解： X = [ 1 2 3 ] X=\left[ \begin{matrix} 1 \\ 2\\ 3 \\ \end{matrix} \right] X=⎣⎡123⎦⎤
5、矩阵乘法
- A = [ a i j ] , 1 ≤ i ≤ m , 1 ≤ j ≤ k A=[a_{ij}], 1\le i\le m, 1\le j\le k A=[aij],1≤i≤m,1≤j≤k
- B = [ b i j ] , 1 ≤ i ≤ k , 1 ≤ j ≤ n B=[b_{ij}], 1\le i\le k, 1\le j\le n B=[bij],1≤i≤k,1≤j≤n
-
C
=
A
×
B
=
[
c
i
j
]
=
[
∑
p
=
1
k
a
i
p
⋅
b
p
j
]
,
1
≤
i
≤
m
,
1
≤
j
≤
n
\displaystyle C=A\times B=[c_{ij}]=[\sum_{p=1}^k a_{ip}\cdot b_{pj}], 1\le i\le m, 1\le j\le n
C=A×B=[cij]=[p=1∑kaip⋅bpj],1≤i≤m,1≤j≤n
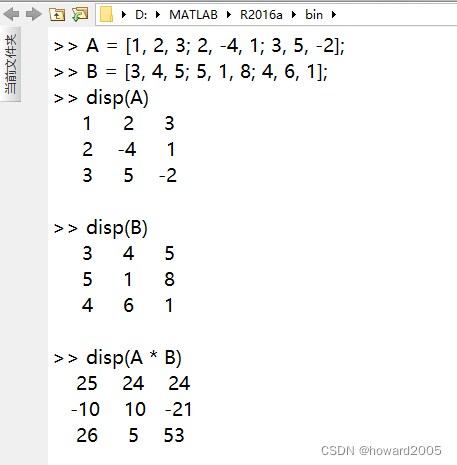
- A ∗ B A * B A∗B的第一个元素 25 = 1 × 3 + 2 × 5 + 3 × 4 25 = 1\times3+2\times 5+ 3\times4 25=1×3+2×5+3×4
6、矩阵点乘
- 矩阵点乘意味着对应元素相乘
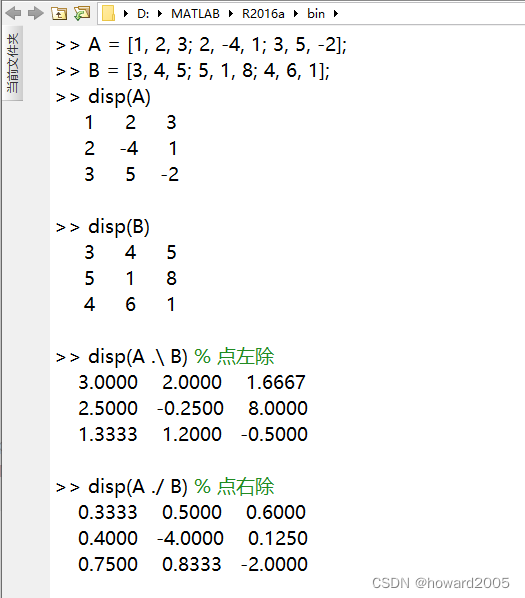
7、矩阵点除
- 矩阵点除意味着对应元素相除
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
