背包问题-最优解

主要是想记录下学习的背包问题
问题描述：
给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品，使得装
入背包中物品的总价值最大?
对于一种物品，要么装入背包，要么不装。所以对于一种物品的装入状态可以取0和1.我们设物品i的装入状态为xi,xi∈ (0,1)，此问题称为0-1背包问题。
数据：物品个数n=5,物品重量w[n]={0，2，2，6，5，4},物品价值V[n]={0，6，3，5，4，6},给定背包容量为10，
我们可以得到一个二维数组。自左下开始向右上看

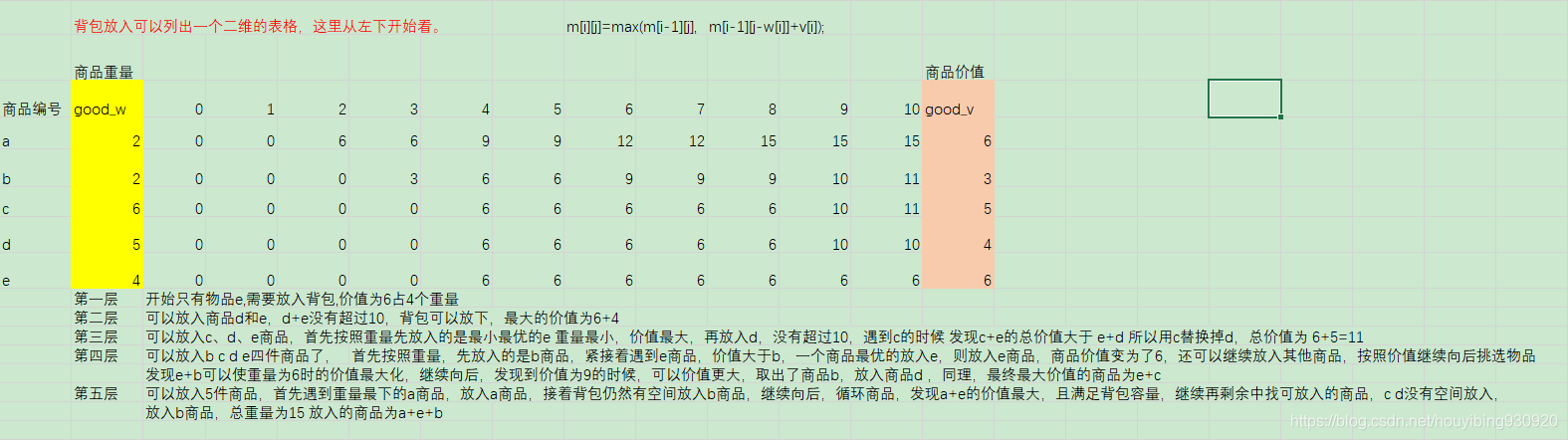
用代码描述如下：

public static void main(String[] args) {
    int [] good_w = {2,2,6,5,4};  //商品重量
    int [] good_v = {6,3,5,4,6}; //商品价值
    int m = 10; //背包容量
    int number = 5;//商品数量
    //初始化二位数组
    int c[][] = new int[number+1][m+1];
    //二维数组第一行第一列填充值0
    for (int i = 0; i < c.length; i++) {
        c[i][0] = 0;
    }
    for (int i = 0; i < c[0].length; i++) {
        c[0][i] = 0
    }
    //二维数组遍历
    for (int i = 1; i < c.length; i++) {
        for (int wj = 1; wj < c[0].length; wj++) {
            if(good_w[i-1]>wj){
                //装不下
                c[i][wj] = c[i-1][wj];
            }else{
                //在装和不装中寻求最优解，取装和不装的最大值
                c[i][wj] = Math.max(c[i-1][wj], c[i-1][wj-good_w[i-1]]+good_v[i-1])
            }
        }
    }
}