仿射变换和透视变换

1 简述仿射变换和透射变换的基本概念，并用实例说明

仿射变换:
仿射变换的表达式一般为：

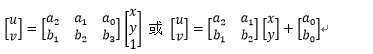
平移、比例缩放和旋转变换都是一种称为仿射变换的特殊情况。
具有如下性质：
（1）仿射变换有6个自由度（对应变换中的6个系数），因此，仿射变换后互相平行直线仍然为平行直线，三角形映射后仍是三角形。但却不能保证将四边形以上的多边形映射为等边数的多边形。
（2）仿射变换的乘积和逆变换仍是仿射变换。
（3）仿射变换能够实现平秱、旋转、缩放等几何变换。
比如我们将一个平面坐标旋转加平移就是仿射变换
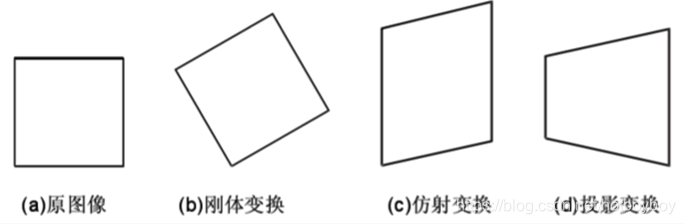
仿射变换是一种二维坐标到二维坐标之间的线性变换，保持二维图形的平直性，保持二维图形的“平直性”（即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平行性”（其实是指保二维图形间的相对位置关系不变，平行线还是平行线，相交直线的交角不变。）。如下图所示

参考链接:
https://blog.youkuaiyun.com/sailinglt/article/details/77196364
https://www.cnblogs.com/bnuvincent/p/6691189.html
透视变换：
本质是将图像投影到一个新的视平面。仿射变换可以理解为透视变换的特殊形式。利用透视中心、像点、目标点三点共线的条件，按透视旋转定律使承影面（透视面）绕迹线（透视轴）旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影几何图形不变的变换。如图所示；

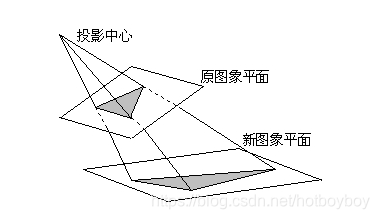
对于透视投影，一束平行于投影面的平行线的投影可保持平行，而不平行于投影面的平行线的投影会聚集到一个点，该点称为灭点。
当在行驶过程中，看向远处，马路两边的白线会向交于一点
两者的关系
仿射变换：二维空间的变换 ； 线性变换 ；已知3对坐标点就可以求得变换矩阵
透视变换：三维空间的变换 ； 非线性变换 ；已知4对坐标点可以求得变换矩阵
参考链接：
https://blog.youkuaiyun.com/Liuqz2009/article/details/61198790
https://blog.youkuaiyun.com/zhanghm1995/article/details/80762274
2 结合图简述图像坐标系、相机坐标系和世界坐标系的定义，并说明三者之间的变换关系

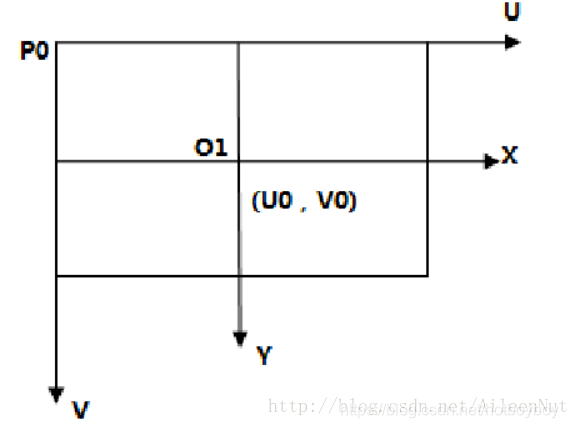
1 像素坐标系
原点：图像左上角P0点
单位：像素
横坐标u：图像数组中的列数
纵坐标v：图像数组中的行数
2 图像坐标系：
在图像像素坐标系下建立以物理单位（以下均假设为mm）表示的坐标系，使像素尺度具有物理意义。
原点：主点（相机光轴与图像平面的交点，一般位于图像平面中心，即图中O1点）
单位：mm/像素
横轴x轴：与像素坐标系下的u轴平行
纵轴y轴：与像素坐标系下的v轴平行
像素坐标系与图像坐标系的转换关系：

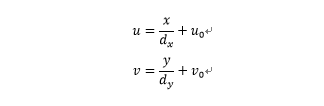
其中，dx为每个像素在横轴x上的尺寸，dy为每个像素在纵轴y上的尺寸。将其写成矩阵形式：

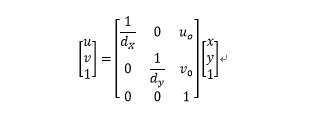
3 相机坐标系

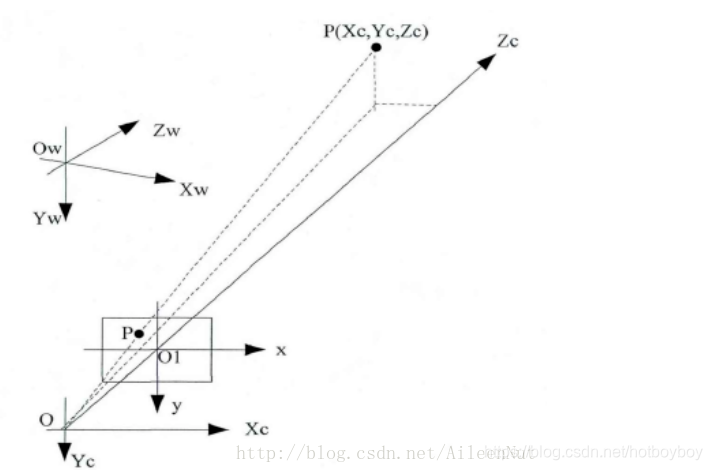
图中：xy平面为图像平面

原点：摄像机光心O点
Xc轴：与图像坐标系x轴平行
Yc轴：与图像坐标系y轴平行
Zc轴：摄像机光轴，与图像平面垂直
OO1=f（焦距）
图像坐标系和相机坐标系的转换关系：

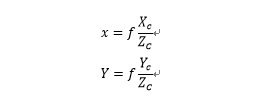
将其写成矩阵形式:

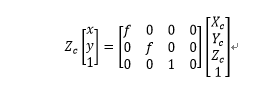
4 世界坐标系
世界坐标系用来描述相机的位置，即相机坐标系原理图中的Ow-XwYwZw坐标系。
相机坐标系与世界坐标系的转换关系：

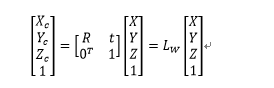
其中:
R为旋转矩阵，是x，y，z三个轴向旋转矩阵的乘积，即R=RxRyRz。
T为平移向量，表示三个轴向上的平移距离，即T=[Tx,Ty,Tz]（上标表转置）。
Lw为由旋转平移构成的一个4*4的矩阵。
由上述对三个坐标系之间的转换可以推导得到图像像素坐标系和世界坐标系的转换关系：

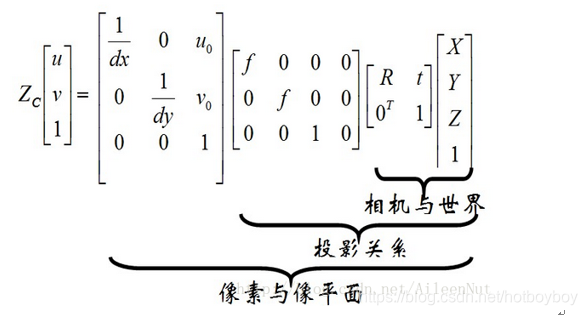
参考链接：https://blog.youkuaiyun.com/weicao1990/article/details/82688446
3 什么是相机的内、外参数矩阵？实际中你能结合身边的实例（如电脑摄像头、手机镜头）说明这些参数的大致值么？
像素坐标系与物理坐标系的转换关系如图所示：

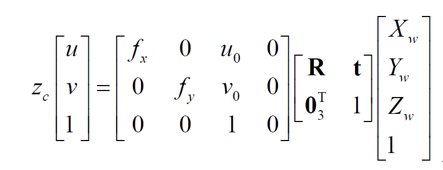
外参：
即为外参矩阵，之所称之为外参矩阵可以理解为只与相机外部参数有关，且外参矩阵随刚体位置的变化而变化。
内参：内参矩阵可以理解为矩阵内各值只与相机内部参数有关，且不随物体位置变化而变化。

参考链接：
https://blog.youkuaiyun.com/qq_30815237/article/details/87530011