二叉搜索树（C语言）

最新推荐文章于 2023-05-27 16:51:54 发布

原创最新推荐文章于 2023-05-27 16:51:54 发布 · 置顶 · 374 阅读

CC 4.0 BY-SA版权

这篇博客介绍了二叉搜索树的概念，它是一棵空树或满足特定排序条件的二叉树。文章详细阐述了二叉搜索树的性质，并通过C语言展示了如何实现关键字的搜索、插入和删除操作，包括递归和非递归方法。对于插入操作，如果关键字已存在则插入失败，否则成功；删除操作则根据具体情况分为多种情况处理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二叉搜索树又称二叉排序树，他或者是一颗空树，或者是具有以下性质的二叉树

1、若它的左子树不为空，左子树上所有节点的值都小于根节点上的值

2、若它的右子树不为空，右子树上所有节点的值都大于根节点上的值

它的左右子树分别为二叉搜索树

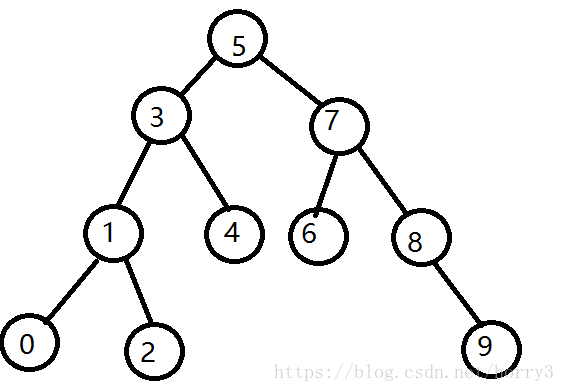
在这里插入图片描述
用搜索关键字的方法先定义

typedef int Key;

在定义结构体：

typedef struct BSTreeNode{
	Key		key;
	struct BSTreeNode *left;
	struct BSTreeNode *right;
}	BSTreeNode;

先查询是否由此关键词
如果找到了，返回 0 表示成功
如果没找到，返回 -1 表示失败

用递归的方法来写就是

int BSTreeSearch(BSTreeNode *root, Key key)
{
	if (root == NULL) {
		return -1;
	}

	if (key == root->key) {
		return 0;
	}
	else if (key < root->key) {
		return BSTreeSearch(root->left, key);
	}
	else {
		return BSTreeSearch(root->right, key);
	}
}

非递归的是：

int BSTreeSearchLoop(BSTreeNode *root, Key key)
{
	BSTreeNode *cur = root;
	while (cur != NULL) {
		if (key == cur->key) {
			return 0;
		}
		else if (key < cur->key) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	return -1;
}

在二叉树中插入一个关键字，要改变参数，所以要传地址用　＊＊
如果重复，插入失败，返回 -1
如果不重复，插入成功，返回 0

非递归方法

int BSTreeInsertLoop(BSTreeNode **pproot, Key key)
{
	assert(pproot != NULL);
	BSTreeNode *cur = *pproot;
	BSTreeNode *parent = NULL;

	while (cur != NULL) {
		if (key == cur->key) {
			// key 重复 插入失败。
			return -1;
		}

		parent = cur;
		if (key < cur->key) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	BSTreeNode *node = (BSTreeNode *)malloc(sizeof(BSTreeNode));
	node->key = key;
	node->left = NULL; node->right = NULL;

	if (parent == NULL) {
		// 对空树做插入
		*pproot = node;
	}
	else if (key < parent->key) {
		parent->left = node;
	}
	else {
		parent->right = node;
	}

	return 0;
}

递归法

int BSTreeInsert(BSTreeNode **pproot, Key key)
{
	if (*pproot == NULL) {
		BSTreeNode *node = (BSTreeNode *)malloc(sizeof(BSTreeNode));
		node->key = key;
		node->left = NULL; node->right = NULL;
		*pproot = node;
		return 0;
	}

	if (key == (*pproot)->key) {
		return -1;
	}

	if (key < (*pproot)->key) {
		return BSTreeInsert(&(*pproot)->left, key);
	}
	else {
		return BSTreeInsert(&(*pproot)->right, key);
	}
}

删除关键字：
如果找到了，就成功删除，返回０
如果没有找到，就返回－１
删除的时候分为三种情况
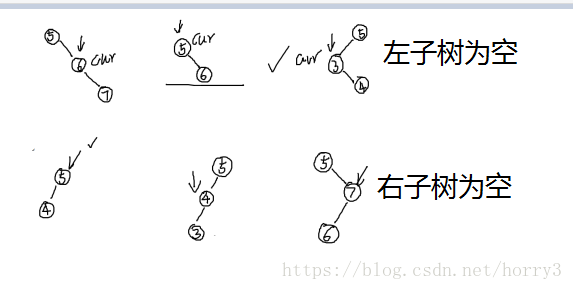
在这里插入图片描述

int BSTreeRemoveLoop(BSTreeNode **pproot, Key key)
{
	BSTreeNode *cur = *pproot;
	BSTreeNode *parent = NULL;
	while (cur != NULL) {
		if (key == cur->key) {
			// 真正删除
			if (cur->left == NULL) {
				if (parent == NULL) {
					// 要删除的是根结点
					*pproot = cur->right;
				}
				else if (key < parent->key) {
					parent->left = cur->right;
				}
				else {
					parent->right = cur->right;
				}
				free(cur);
				return 0;
			}
			else if (cur->right == NULL) {
				if (parent == NULL) {
					// 要删除的是根结点
					*pproot = cur->left;
				}
				else if (key < parent->key) {
					parent->left = cur->left;
				}
				else {
					parent->right = cur->left;
				}
				free(cur);
				return 0;
			}
			else {
				// 替换法删除
				// 左右孩子都不为空

				// 找右子树中最小的一个
				BSTreeNode *del = cur->right;
				BSTreeNode *delParent = cur;
				while (del->left != NULL) {
					delParent = del;
					del = del->left;
				}

				cur->key = del->key;

				if (delParent == cur) {
					delParent->right = del->right;
				}
				else {
					delParent->left = del->right;
				}
				free(del);
				return 0;
			}
		}

		parent = cur;
		if (key < cur->key) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	return -1;
}