线性回归_线性回归方程公式wtx-优快云博客

本文详细介绍了线性回归的基本形式、成本函数及其多种变体，包括普通最小二乘法、岭回归、Lasso和弹性网络。通过对误差的平方和最小化来寻找最佳函数匹配，同时探讨了概率解释。文章还讨论了求解方法，如梯度下降法的不同策略，并特别提到了岭回归中L2正则化的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基本形式

线性模型试图学的一个通过属性的线性组合来进行预测的函数，函数形式为：
$f(x)=w_1x_1+w_2x_2+...+w_dx_d+b$
向量表示
$f(x)=w^Tx+b$
我们的目标是学习得到 $w$ 和 $b$ ，这样模型就确定了。
这里有一个小技巧，我们令 $x_0=1$ 这样，模型就可以进行简化、统一为
$h_\theta(x)=\theta_0x_0+\theta_1x_1+...+\theta_nx_n=\theta^Tx$
$\theta_0$ 为截距，在sklearn中为intercept_

Cost function

定义

线性回归的损失函数有很多种形式，但都可以称为最小二乘法。最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。 （最小二乘法）
下面以sklearn的线性回归为例：

普通最小二乘法（RSS）

$J(\theta)=\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$

岭回归（Ridge）

使用了L2正则
$J(\theta)=\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\alpha\sum_{j=0}^n\theta_j^2$

Lasso

使用了L1正则
$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\alpha\sum_{j=0}^n|\theta_j|$

弹性网络

结合了L1和L2
$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\alpha\rho\sum_{j=0}^n|\theta_j|+\frac{\alpha(1-\rho)}{2}\sum_{j=0}^n\theta_j^2$

由来（概率解释）

假设目标变量和输入值存在如下等量关系
$y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)}$
其中 $\epsilon^{(i)}$ 是误差项。假设 $\epsilon^{(i)}$ 是独立的且符合高斯分布 $\epsilon^{(i)}\sim N(0, \sigma^2)$
故
$p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(\epsilon^{(i)})^2}{2\sigma^2})\\ p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2})$
使用最大似然估计（MLE）
$L(\theta) =\prod_{i=1}^{m} p(y^{(i)}|x^{(i)};\theta) =\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2})$
取对数
$log\ L(\theta) =log\ \prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2})\\ log\ L(\theta)=\sum_{i=1}^{m}log\ \frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum_{i=1}^{m}(y^{(i)} - \theta^Tx^{(i)})^2$
第一项为常数项，要使 $log\ L(\theta)$ 最大，所以要第二项尽可能的小，所以要使
$\frac{1}{2}\sum_{i=1}^{m}(y^{(i)} - \theta^Tx^{(i)})^2$
尽可能的小

求解

有了Cost Function之后，我们就需要对目标函数进行求解

普通最小二乘法

正规方程

以西瓜书的推导为范本 P55 3.11
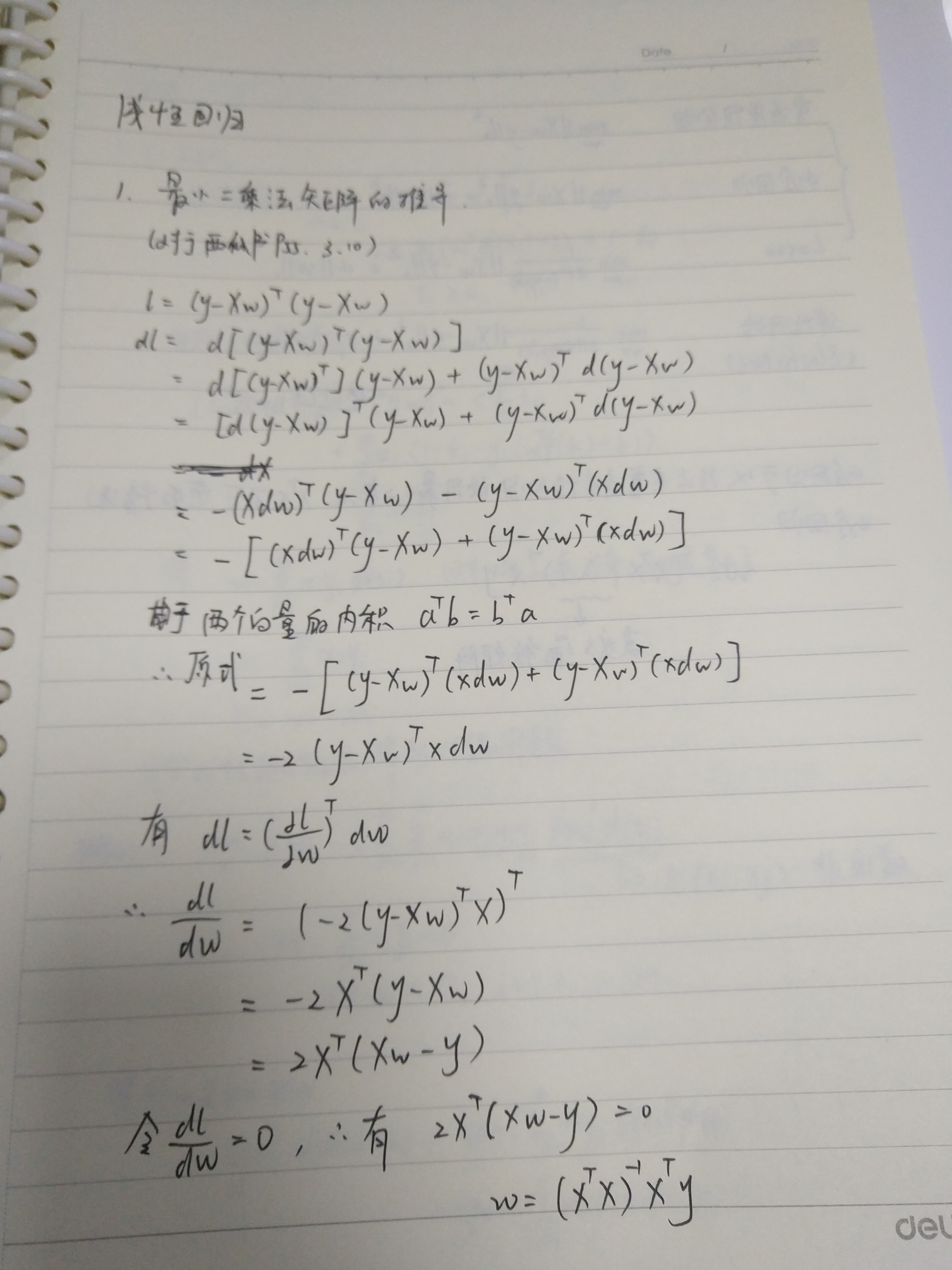
在这里插入图片描述

梯度下降

这里以吴恩达的为范本，吴恩达的损失函数为 $J(\theta)=\frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$
梯度下降就是从某一个 $\theta$ 的初始值开始，然后逐渐重复更新
$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)$
其中
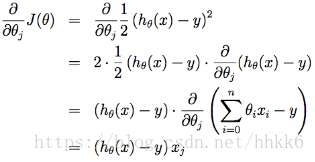
在这里插入图片描述

批量梯度下降(Batch Gradient Descent)

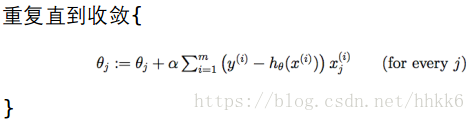
在这里插入图片描述
优点：得到全局最优解
缺点：当样本数目很多时，训练过程会很慢

随机梯度下降(Stochastic Gradient Descent)

也叫作增量梯度下降法（incremental gradient descent）
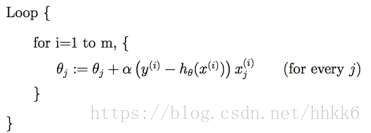
在这里插入图片描述
随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。
随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。
对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。
对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。
优点：训练速度快
缺点：准确度下降，可能跳出最优解，不是全局最优