深度学习碎碎念(一)

深度学习碎碎念(一)

1️⃣理解高维数据

参考blog：关于深度学习高维矩阵的形象化理解_高维矩阵百度百科-优快云博客

💫高维数据的理解：每一维都是对数据的一次分类

例如现有12个苹果样本，被三次分类，即三维数据，如下图

• 黑 = [[黑南]，[黑北]]
• 白 = [[白南]，[白北]]
• 紫 = [[紫南]，[紫北]]

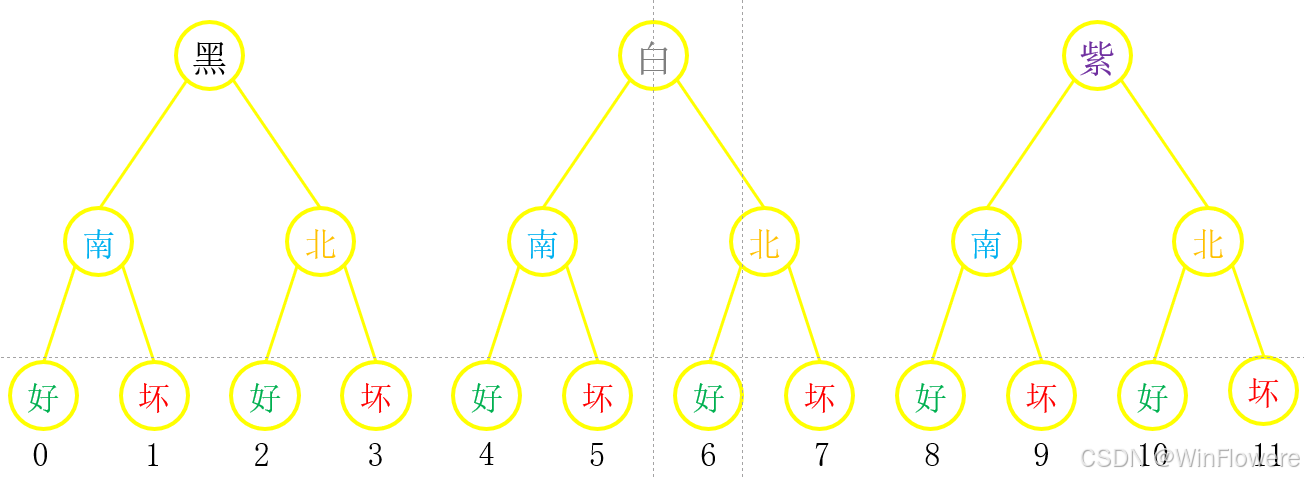
我们用张量表示这些三维数据：

import torch
import pprint
arr = torch.arange(12, dtype=torch.int32).reshape(3, 2, 2)
>>> tensor([[[ 0,  1],
         	 [ 2,  3]],

        	[[ 4,  5],
         	 [ 6,  7]],

        	[[ 8,  9],
         	 [10, 11]]], dtype=torch.int32)

对其进行前两维的交换，即permute操作，permute操作相当于交换了数据被分类的顺序，如苹果是原先是先按颜色分类再按产地分类，经过permute操作后变为先按产地分类再按颜色分类，因此，数据的组织将会变为：

• 南 = 南黑 + 南白 + 南紫，用数组形式表示就是南 = [[南黑]，[南白]，[南紫]]

• 北 = 北黑 + 北白 + 北紫，用数组形式表示就是北 = [[北黑]，[北白]，[北紫]]

让我们用代码验证一下，结果如下，另有图形化展示，说明例如原先位于数组[2,0,1]处的是9，语义含义是紫南好，交换维度后应该变成南紫好，对应交换维度后的数组位置就是[0,2,1]，可以看到也是9

arr_per = torch.permute(arr, (1, 0, 2))
>>> tensor([[[ 0,  1],
         	 [ 4,  5],
         	 [ 8,  9]],

        	[[ 2,  3],
         	 [ 6,  7],
         	 [10, 11]]], dtype=torch.int32)

理解了permute操作，让我们再来顺着这条线来理解一下flatten操作，flatten操作的结果是对数组的某一维进行展平操作，这里我用代码分别对上述经过permute操作后的三维数据的三个维度进行flatten，结果如下

arr_per
>>> tensor([[[ 0,  1],
         	 [ 4,  5],
         	 [ 8,  9]],

        	[[ 2,  3],
         	 [ 6,  7],
         	 [10, 11]]], dtype=torch.int32)

arr_flat_0 = torch.flatten(arr_per, 0)	# 对第一维进行flatten
>>> tensor([ 0,  1,  4,  5,  8,  9,  2,  3,  6,  7, 10, 11], dtype=torch.int32)

arr_flat_1 = torch.flatten(arr_per, 1) 	# 对第二维进行flatten
>>> tensor([[ 0,  1,  4,  5,  8,  9],
        	[ 2,  3,  6,  7, 10, 11]], dtype=torch.int32)

arr_flat_2 = torch.flatten(arr_per, 2)	# 对第三维进行flatten
>>> tensor([[[ 0,  1],
         	 [ 4,  5],
         	 [ 8,  9]],

        	[[ 2,  3],
         	 [ 6,  7],
         	 [10, 11]]], dtype=torch.int32)

在这里我发现：

• 对数组的某一维进行展平，其后面的维度都会“消失”，而只剩下之前的维度
• “消失”的维度会以乘积的形式表现在被faltten后数组的最后一维
• 在保留的维度中，这一维的数据仍然会按照原先分类的顺序进行排列(像是深度优先搜索，可以从这个角度思考一下数据的排列方式)

下面，让我来解释一下这几个规律：

首先，以代码为例，

• 当我们对第一维进行flatten操作时，原先[2,3,2]的三维数组变成了长度为12的一维数组；

• 当我们对第二维进行flatten操作时，原先[2,3,2]的三维数组变成了[2,6]的二维数组；

• 当我们对第三维进行flatten操作时，原先[2,3,2]的三维数组保持不变。

进一步观察，

• 在被进行第一维flatten操作后的数组中，按照次序可写为[南黑,南白,南紫,北黑,北白,北紫];
• 在被进行第二维flatten操作后的数组中，按照次序可写为[[南黑,南白,南紫],[北黑,北白,北紫]];
• 在被进行第三维flatten操作后的数组中，按照次序可写为[[[南黑],[南白],[南紫]],[[北黑],[北白],[北紫]]];

在理解了flatten操作后，我们还需要对sum操作有一个直观的理解，还是一样，先跑一遍代码

arr_per
>>> tensor([[[ 0,  1],
         	 [ 4,  5],
         	 [ 8,  9]],

        	[[ 2,  3],
         	 [ 6,  7],
         	 [10, 11]]], dtype=torch.int32)
         	 
arr_per.sum(dim=0)
>>> tensor([[ 2,  4],
        	[10, 12],
        	[18, 20]])

arr_per.sum(dim=1)
>>> tensor([[12, 15],
        	[18, 21]])

arr_per.sum(dim=2)
tensor([[ 1,  9, 17],
        [ 5, 13, 21]])

还是一样，先放规律，再解释原因

• 对数组的某一维进行sum操作，这一维会消失，其他维均会保留下来
• 消失的这一维，会在其后一维度的基础上进行求和

解释一下上述规律：

首先，我们可以看到：

• 当我们对数组的第一维进行sum操作时，原先[2,3,2]的数组变成了[3,2]的数组
• 当我们对数组的第二维进行sum操作时，原先[2,3,2]的数组变成了[2,2]的数组
• 当我们对数组的第三维进行sum操作时，原先[2,3,2]的数组变成了[2,3]的数组

进一步观察：

• 在被进行第一维sum操作后的数组中，按照次序可写为[[黑好,北好],[白好,白坏],[紫好，紫坏]]，其中，黑好=南黑好+北黑好，其余类似；
• 在被进行第一维sum操作后的数组中，按照次序可写为[[南好,南坏],[北好,北坏]]，其中，南好=南黑好+南白好+南紫好；
• 在被进行第一维sum操作后的数组中，按照次序可写为[[南黑,南白,南紫],[北黑,北白,北紫]]，其中，南黑=南黑好+南黑坏。

总结：permute操作是交换数据的分类顺序，flatten操作是合并按某一维分类的数据，但其内部仍然存在后续维度分类的顺序，sum操作则是消除某一分类标准

🙇深度剖析计算机视觉领域的高维数据

一般来说，计算机视觉领域的高维数据一般由批量大小、多视角、特征、图像的高宽组成，形式如下
$$data=B\times N\times C\times H\times W$$
也就是说图像数据通常先被分为第几个图像(组)，这些个图像(组)再被分为哪一个视角，在某一视角下按照第几个特征进行分类，到特征以下就很难用分类说清了，因为我们通常把单个图像大小的数组视为最小单元，也就是说，其实在计算机领域，图像数据通常按照前几维进行分类，而后的H,W只是为了方便定位图像中某个具体位置的某个特征

2️⃣理解1x1卷积

参考blog：卷积到底是如何操作的？1x1卷积？参数如何计算？_相同的卷积核为什么输出不同的特征图-优快云博客

3️⃣计算卷积后的图像大小

设原图像的大小为$(W,H)$，卷积核的大小为$(F,F)$，步幅为$S$，Padding为$P$，经过卷积后的图像大小为$(W_f,H_f)$，则有公式：

$$\begin{array}{rl}{W}_f& =\frac{W+2P-F}{S}+1\\ H_f& =\frac{H+2P-F}{S}+1\end{array}$$