Manacher 最长回文子串

最新推荐文章于 2025-07-22 10:53:50 发布

Sanzo00

最新推荐文章于 2025-07-22 10:53:50 发布

阅读量287

点赞数

CC 4.0 BY-SA版权

分类专栏： ACM

本文链接：https://blog.youkuaiyun.com/henuyh/article/details/87694074

ACM 专栏收录该内容

260 篇文章

订阅专栏

本文深入解析Manacher算法，一种高效求解最长回文子串问题的方法。通过在原字符串中插入特殊字符，算法能够同时处理奇数和偶数长度的回文串，利用已知回文半径加速后续字符的回文串半径计算，极大提升了查找效率。

用途

求最长回文串，过程中更新 $m a x (M a x l e n ， R L [i] - 1)$
求回文串的数量， $∑i=0lenRL[i]2\sum_{i=0}^{len}\frac{RL[i]}{2}$

$R L [i]$ ：关于i的回文半径
$M a x R i g h t$ ：pos能到达的最右端的位置
$M a x L e n$ ：记录答案

首先在原字符串中插入字符“#”
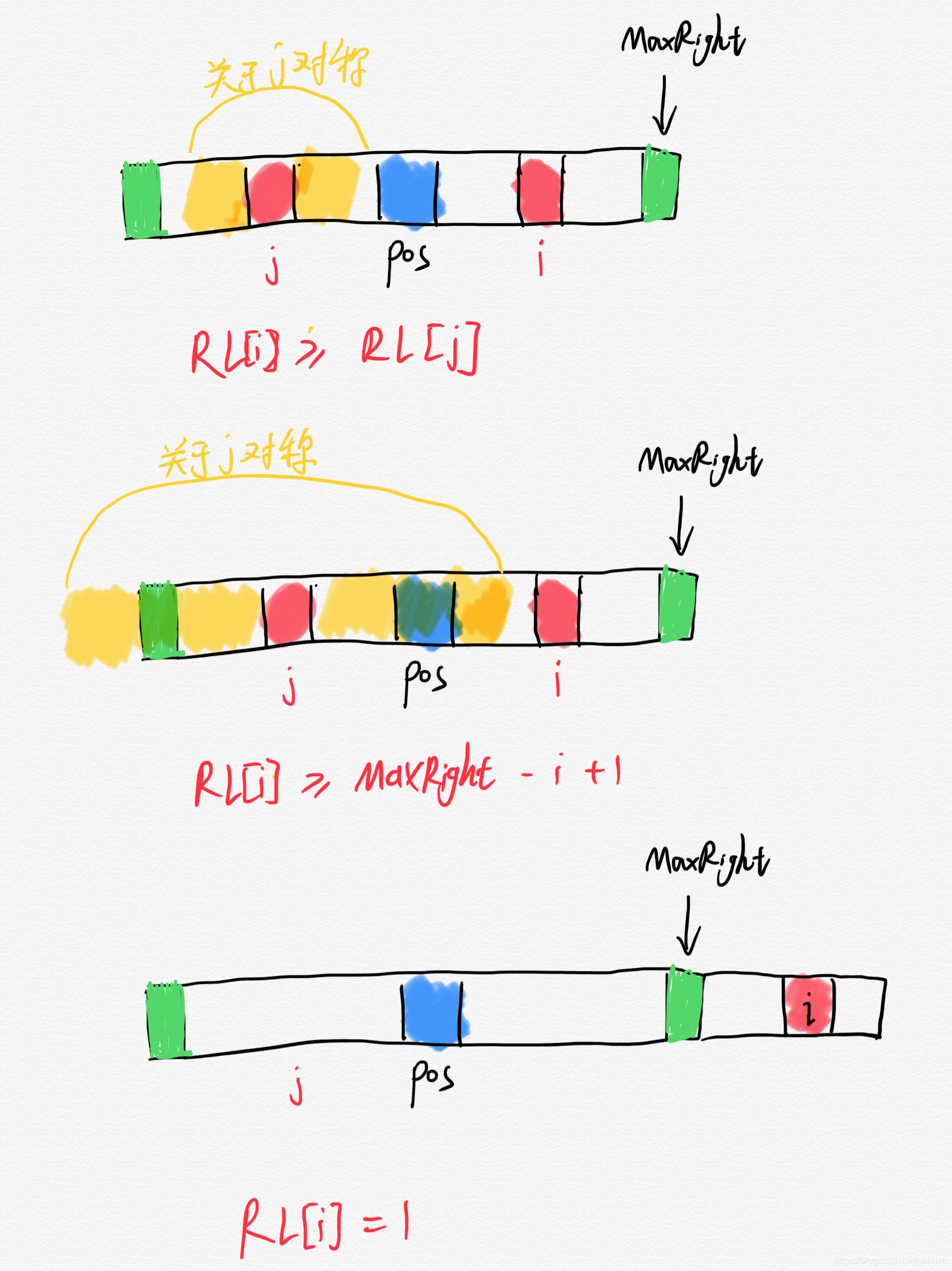
例如：“abba” -> "#a#b#b#a#"这样不影响回文串，好处是可以同时解决长度为奇偶的字符串，而且(回文半径 - 1)就是原来的回文串长度
问题转化为如何高效的求每个字符的回文串半径，当我们知道pos能到达的最右端位置 $M a x R i g h t$ ，我们继续向后枚举字符串求它的回文半径，我们关心的是i这个位置是在MaxRight的左边还是右边，在左边分为两种情况，右边一种情况。
求出来最小值之后再向两边扩展得到最长的回文半径，然后更新 $p o s$ ， $M a x R i g h t$ 。

在这里插入图片描述

int RL[maxn << 1];
int Manacher(string s) {
	string t;
	for (int i = 0; i < (int)s.size(); ++i) {
   		t += s[i];
   		t += '#';
   	}
   	s = "#" + t;
   	int MaxRight = 0, pos = 0, MaxLen = 0;
   	for (int i = 0; i < (int)s.size(); ++i) {
   		if (i < MaxRight)	RL[i] = min(RL[2 * pos - i], MaxRight - i + 1); // 好多这里写的是 MaxRight - i，个人感觉根据算法思想应该+1计算长度。
   		else 	RL[i] = 1;
   		int l = i - RL[i];
   		int r = i + RL[i];
   		while (l >= 0 && r < (int)s.size() && s[l] == s[r])	{
   			RL[i] += 1;
   			l = i - RL[i];
   			r = i + RL[i];
   		}
   		if (RL[i] + i - 1 > MaxRight) {
   			MaxRight = RL[i] + i - 1;
   			pos = i;
   		}
   		MaxLen = max(MaxLen, RL[i]);
   	}
   	return MaxLen - 1;
}

int RL[maxn << 1];
char s[maxn], t[maxn << 1];
int Manacher(char *s) {
	if (s[strlen(s) - 1] == '\n')	s[strlen(s) - 1] = '\0';
	int lens = strlen(s), len = 0;
	t[len++] = '#';
	for (int i = 0; i < lens; ++i) {
   		t[len++] = s[i];
   		t[len++] = '#';
   	}
   	int MaxRight = 0, pos = 0, MaxLen = 0;
   	for (int i = 0; i < len; ++i) {
   		if (i < MaxRight)	RL[i] = min(RL[2 * pos - i], MaxRight - i + 1); // 好多这里写的是 MaxRight - i，个人感觉根据算法思想应该+1计算长度。
   		else 	RL[i] = 1;
   		int l = i - RL[i];
   		int r = i + RL[i];
   		while (l >= 0 && r < len && t[l] == t[r])	{
   			RL[i] += 1;
   			l = i - RL[i];
   			r = i + RL[i];
   		}
   		if (RL[i] + i - 1 > MaxRight) {
   			MaxRight = RL[i] + i - 1;
   			pos = i;
   		}
   		MaxLen = max(MaxLen, RL[i]);
   	}
   	return MaxLen - 1;
}