本文详细介绍了Logistic回归，包括其基本思想、Sigmoid函数的作用、寻找最佳回归参数的方法——梯度上升/下降算法，以及通过代码实现模型训练。通过对Sigmoid函数的分析，展示了Logistic回归如何进行概率估计和分类。最后，提供了使用梯度上升法训练Logistic回归模型的Python代码示例。
逻辑回归 logistic regression
1、概述
主要思想：根据现有的数据对分类边界线建立回归公式（最佳拟合线，这个拟合过程称作为回归），以此进行分类
如下线性函数z，x为输入数据，w为相应的系数。
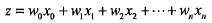
向量写法 Z = W^T*X ，向量X为分类器的输入值，向量W是我们要找到的最佳拟合参数。
得到最佳拟合参数W后， sigmoid(z) > 0.5 分类成1， 否则分类到0
2、Sigmoid 函数
我们想要的回归函数，能接受所有的输入并能够预测出类别。例如两个类别的情况下，函数输出0或1。这样性质的函数，想到
的是单位阶跃函数（海维塞德阶跃函数），而海维塞德阶跃函数的问题是，该函数在跳跃点上从0瞬间跳跃到1，这个瞬间过程有时很
难处理。有幸，我们找到一个函数由此性质，并数学上比较容易处理，这就是sigmoid函数。
Sigmoid 函数，一种阶跃函数，值为0到1之间，如下：
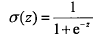
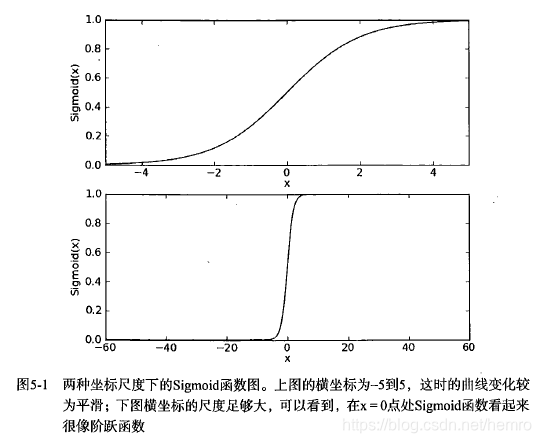
X的尺度足够大时就像0和1之间的阶跃函数。
为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和带入sigmoid函数中，
进而得到一个范围在0~1
最低0.47元/天 解锁文章
扫一扫
1614
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
