机器学习算法 无监督学习 算法

 本文介绍无监督学习算法：

 - 聚类算法

 - Apriori算法

 - FP-growth 算法

 因时间关系，就简单介绍其原理，不涉及实例和代码
 

1 聚类算法

 聚类（Clustering）与分类（classification）的最大不同在于，分类的目标事先已知，而聚类不一样，因产生结果和分类相同，

只是类别没有预先定义，所以聚类也有时叫无监督分类（Unsupervised classification）

 所谓无监督学习是指事先并不知道要寻找的内容，即没有目标变量。聚类将数据点归到多个簇中，其中相似数据点处于同一簇，

而不相似数据点处于不同簇中。聚类中可以使用多种不同的方法来计算相似度。

 

1.1 K-均值聚类算法

 一种广泛使用的聚类算法是K-均值算法，其中K是用户指定的要创建的簇的数目。K-均值聚类算法以K个随机质心开始。算法会计算

每个点到质心的距离。每个点会被分配到距其最近的簇质心，然后紧接着基于新分配到簇的点更新簇质心。以上过程重复数次，直到簇质

心不再改变。

 优点：容易实现

 缺点：可能收敛到局部最小值，在大规模数据集上收敛较慢。

 适用数据类型：数据型数据

 实现思路：

  随机设定K个簇质心点，然后最近原则进行分类（簇），重新计算质心（族所有点的均值作为簇心），重复过程直到没有变化为止

 
比如，如下图，先随机选择两个质心点（红色圈圈）

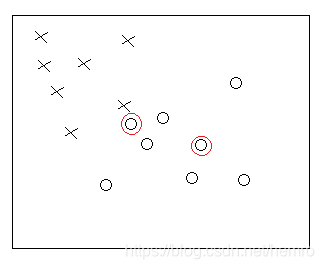
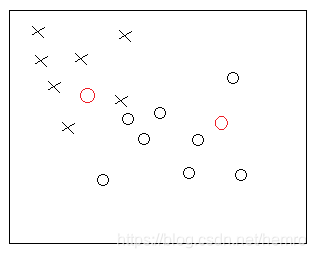
然后把所有点遍历一遍，并把它分给最近的那个质心的簇。第一次计算结果如下

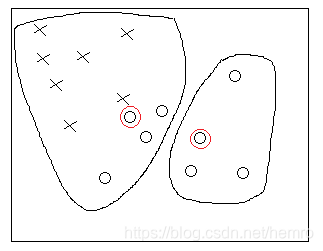
重新计算，簇质心点，大致如下

第二轮分配簇结果

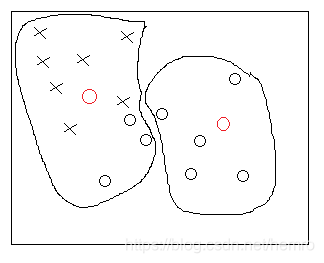
继续重新计算质心，分簇，直到无变化为止

 

1.2 二分K-均值算法

 克服k-均值算法收敛于局部最小值的问题

 实现思路：

  先把所有点分成一个簇

  每次当前的簇，寻找二分后误差最低的簇，对其进行二分

  重复第二步，直到达到簇的个数达到K

 

2 Apriori算法

 关联分析是一种在大规模数据集中寻找有趣的任务。这些关系有有两种形式：频繁项集或关联规则。

频繁项集（frequent imtem sets）是经常出现在一起的物品的集合，关联规则（association rules）暗示两种物品之间可能存在

很强的关系。

 先得到频繁项集，基础上计算关联规则
 

2.1 频繁项集原理

  - 计算单个元素集（C1）的支持度，去掉低于最小支持度的元素，得到L1

  - 构建2（K+1）个元素组成的候选项列表C2（Ck+1），由L1（Lk）原则组合去掉重复的，计算C2（Ck+1）的支持度并去掉

不符合条件的，得到L2（Lk+1）

  - 循环到Lk+1空为止

 

2.2 关联规则原理

 直接看实现比较好理解，这里忽略

 
 

3 FP-growth 算法

 
 比较高效的发现频繁项集的方法，比较高效的发现频繁项集的方法：先构建FP树，再从FP数据挖掘频繁项集

3.1 先构建FP树

 原理：遍历两次，

 第一次遍历计算每个元素的出现频率并去掉不符要求的。生成一个元素header列表。

 第二次遍历，对首先对每一个项集去掉非频繁元素，按出现频率进行排序。按排好的新项集的原色从频率高到底，逐步添加到FP-

tree中，方法就是当前元素节点的child技术加1，否则新创建child节点。此外header 列表对每个元素形成一个列表(第一个出现时

header列表执行该元素，之后插入到链表未中)
 

3.2 从FP数据挖掘频繁项集

 - 抽取条件模式基（前缀路径）

 - 创建条件FP树

 实现原理：

  findPrefixPath获取一个元素的所有前缀路径(条件模式基)

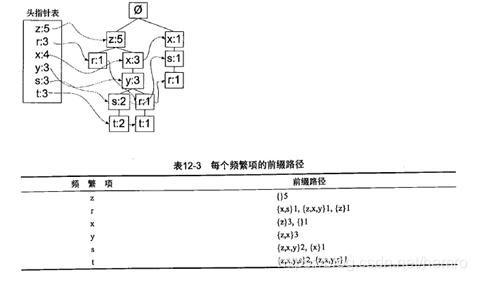
 mineTree 创建条件FP树，从头指针列表低端开始，每一个元素进行获取前缀路基，使用前缀路基构建新tree。对新建tree每个元素

再进行mineTree（一直递归到新建tree为止）。 频繁项集取prefix+当前的元素。prefix从空开始，逐步增加，如上图t，其prefix依次

[null]、 [t]、[t、y]、[t、x]、等等，