高精度乘法

文章目录

前言

一、什么是高精度乘法？

二、高精度乘法的原理

1.问题引入

2.算法分析

3.代码实现

---

前言

今天要和大家分享一个编程中的“大杀器”——高精度乘法！无论是处理巨大的数据，还是解决算法竞赛中的难题，高精度乘法都能派上用场。接下来，我会详细解释什么是高精度乘法，并附C++的实现代码。

一、什么是高精度乘法？

高精度乘法，顾名思义，就是能处理超大数字乘法的算法。在普通的编程环境中，整数类型（如int、long等）都有一个固定的范围。当数字超出这个范围时，就会发生溢出，导致计算结果错误。而高精度乘法算法则能够突破这个限制，让我们能够准确地计算超大数字的乘积。

二、高精度乘法的原理

1.问题引入

从键盘读入两个1000位以内的非负整数，并输出两数之积

2.算法分析

由于数据过大，我们无法用传统方法实现乘法运算。由此，高精度乘法通常通过模拟手工加法的实现。首先让我们回顾一下竖式乘法：

             

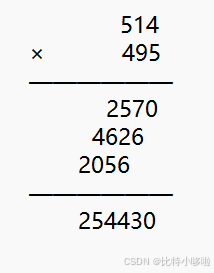
数	第6位	第5位	第4位	第3位	第2位	第1位
a				5	1	4
b				4	9	5
a*b[1]				25	5	20
a*b[2]			49	9	36
a*b[3]		20	4	16
中间产物		20	49	50	41	20
处理进位	2	5	4	4	3	0
结果	2	5	4	4	3	0

a[1]*b[1]的贡献在中间产物的第1位

a[2]*b[1]的贡献在中间产物的第2位 ......

a[1]*b[2]的贡献在中间产物的第2位

a[2]*b[2]的贡献在中间产物的第3位 ......

不难发现，a[i]+b[j]的贡献全部在中间产物的第i+j-1位上。依据这个性质，我们可以将所有的贡献算出来，最后一并处理所有的进位问题。

3.代码实现

#include<iostream>
#include<string>
#define maxn 1500
using namespace std;
int a[maxn], b[maxn], c[maxn];

int main()
{
//输入数据
	string num1, num2;
	cin >> num1 >> num2;

//将字符串转为数字存入数组中
	int len1 = num1.length(), len2 = num2.length();
	for (int i = len1 - 1; i >= 0; i--)
		a[len1 - i] = num1[i] - '0';
	for (int i = len2 - 1; i >= 0; i--)
		b[len2 - i] = num2[i] - '0';

//模拟过程得出中间产物
	for (int i = 1; i <= len1; i++)
		for (int j = 1; j <= len2; j++)
			c[i + j - 1] += a[i] * b[j];

	int len = len1 + len2;//乘积的位数不超过两数的位数之和
//处理进位
	for (int i = 1; i <= len; i++)
	{
		c[i + 1] += c[i] / 10;
		c[i] %= 10;
	}

//去掉前面的0
	while (!c[len])
		len--;

//输出
	for (int i = max(i, len); i >= 1; i--)
		cout << c[i];

	cout << endl;
	system("pause");
}