最小生成树之kruskal算法

最新推荐文章于 2023-10-13 13:42:36 发布

原创最新推荐文章于 2023-10-13 13:42:36 发布 · 154 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#北邮oj

本文深入探讨了最小生成树算法的实现，通过定义边和树的结构，利用sort函数进行排序，实现了一种有效的求解最小生成树的方法。文章详细介绍了如何通过遍历边集合，检查连接的两个顶点是否属于同一棵树，如果不是，则将它们合并并累加边的权重，最终得到最小生成树的总权重。

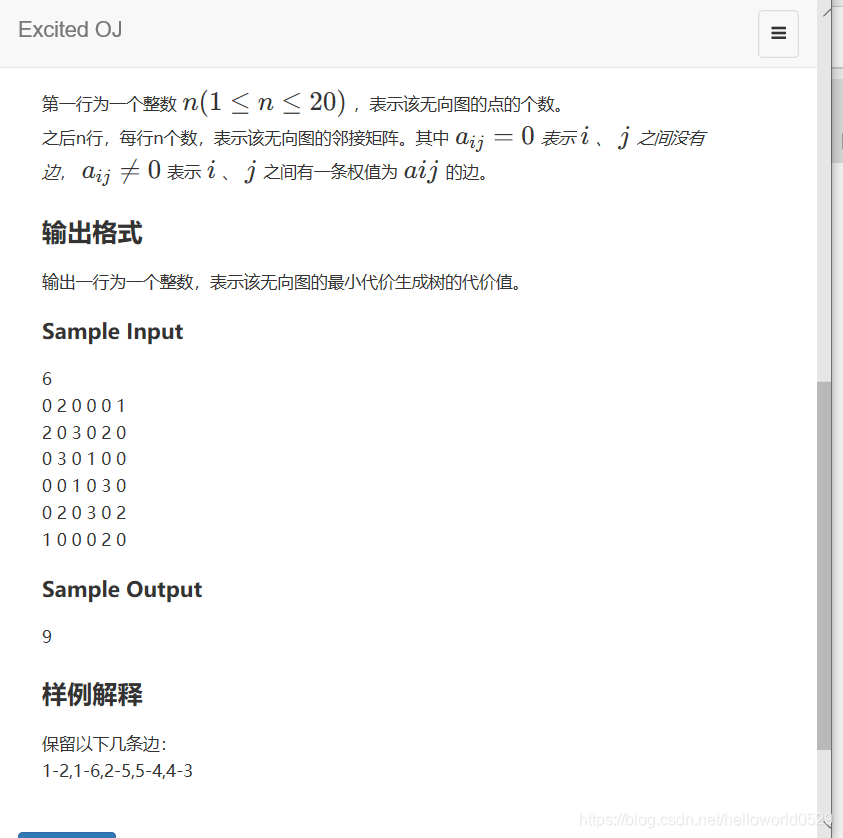
在这里插入图片描述

知识点：

1.sort函数【a，b）
sort（首地址，尾地址+1，cmp）
2.边的数量n*n所有的和边有关的矩阵都要开这么大

思路：

把树看成矩阵，treenum存每个树里元素个数

#include<iostream>
#include<algorithm>
#define MAXSIZE 405
//边的数目n*n，对应的各类矩阵也应该是n*n
using namespace std;
typedef struct {
	int w;
	int head, tail;
}edge;
edge E[MAXSIZE];
int tree[MAXSIZE][MAXSIZE];
int treenum[MAXSIZE];
bool cmp(edge x, edge y);
int main()
{
	int n,cnt=0,sum=0;
	//int cnt1 = 0;
	cin >> n;
	int a[25][25];
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			cin >> a[i][j];
	for (int i = 1; i <= n; i++)
		for (int j = i; j <= n; j++)
			if (a[i][j])
			{
				E[++cnt].w = a[i][j];
				E[cnt].head = i;
				E[cnt].tail = j;
				//cnt1++;
				//cout << i << " " << j << endl;
			}
	for (int i = 1; i <= n; i++)
	{
		tree[i][1] = i;
		treenum[i] = 1;
	}

	sort(E+1, E + cnt+1, cmp);//升序排列//sort(首地址，尾地址+1）
	//cout << cnt1 << endl;
	//for (int i = 1; i <= cnt+1; i++)
		//cout << E[i].w << " ";
	
	for (int i = 1; i <= cnt; i++)
	{
		//cout << "edge" << E[i].w << " " << E[i].head << " " << E[i].tail<<endl;
		int lochead, loctail;
		for (int k1 = 1; k1 <= cnt; k1++)
			for (int k2 = 1; k2 <= cnt; k2++)
			{
			if (tree[k1][k2] == E[i].head&&tree[k1][k2]!=0)
			{
				lochead = k1;
				//cout << k1 << " " << k2 << endl;
			}
			if (tree[k1][k2] == E[i].tail && tree[k1][k2] != 0)
			{
				loctail = k1;
				//cout<< k1 << " " << k2 << endl;
			}

			}
		
		if (loctail != lochead)
		{
			sum += E[i].w;
			//cout << "sum" << sum << endl;
			//cout << "loctail  lochead" << loctail << lochead << endl;
			for (int t1 = 1; t1 <= treenum[loctail]; t1++)
			{
				int temp = treenum[lochead];
				tree[lochead][++temp] = tree[loctail][t1];
				//cout << "移动的树" << tree[loctail][t1] << endl;
				tree[loctail][t1] = 0;
				treenum[lochead]++;
			}
		}
	}
	cout << sum;


		


	return 0;
}

bool cmp(edge x, edge y)
{
		/*int c1 = x.w, c2 = y.w;
		if (!c1) c1 = 1e9;
		if (!c2) c2 = 1e9;
		return c1 < c2;
	*/
	if (x.w != 0 && y.w != 0)
		return x.w < y.w;

}