pta题集——找鞍点

一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。

本题要求编写程序，求一个给定的n阶方阵的鞍点。

输入格式：

输入第一行给出一个正整数n（1≤n≤6）。随后n行，每行给出n个整数，其间以空格分隔。

输出格式：

输出在一行中按照“行下标 列下标”（下标从0开始）的格式输出鞍点的位置。如果鞍点不存在，则输出“NONE”。题目保证给出的矩阵至多存在一个鞍点。

题目分析：

一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。

如图所示：

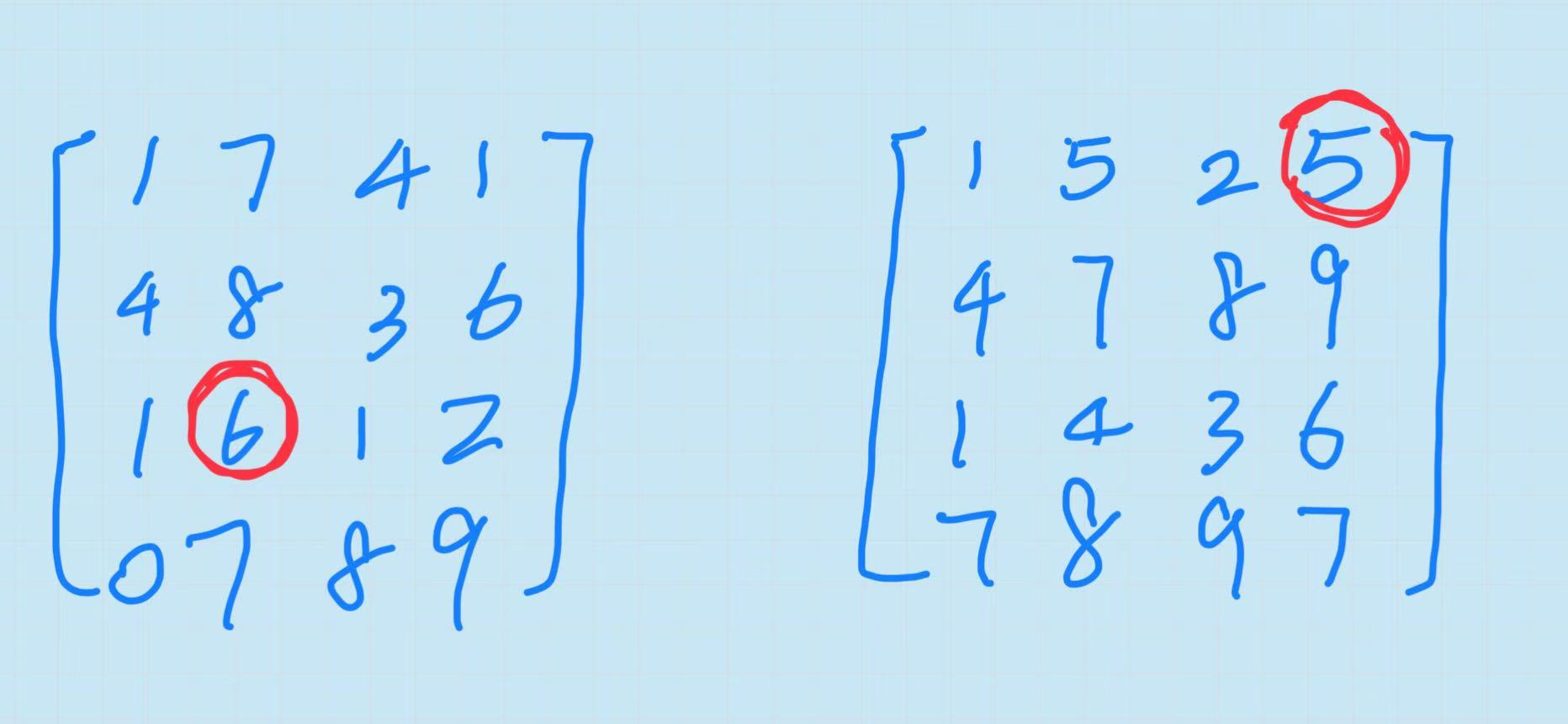
第一个矩阵的鞍点为6，第二个矩阵的鞍点为5，同时要注意第二个矩阵中同一行里有两个相同的最大元素，则要一一进行判断。

解答过程：

数据输入：

n=int(input())
ls=[]
for i in range(n):
    row=list(map(int,input().split()))
    ls.append(row)

读入了正整数n，表示这是一个n*n的矩阵，然后再将矩阵存储进二维列表中。

寻找鞍点及输出部分：

found=0
i=0
while i<n:
    max_num=max(ls[i])
    for j in range(n):
        if ls[i][j]==max_num:
            flag=0
            for k in range(n):
                if ls[k][j]<max_num:
                    flag=1
                    break
            if flag==0:
                print(f"{i} {j}")
                found=1
                break
    if found:
        break
    i+=1
                    
if found==0:
    print("NONE")

定义found变量表示是否找到鞍点

开启循环，遍历矩阵的每行，先找出每行中的最大数字，在遍历此行的过程中，若此行中有元素等于此行的最大数，则将flag置为0（flag用于判断该元素是否为鞍点），记下该元素的列，遍历该元素所在列，若该列中有元素小于该元素，则flag置为1，该元素不是鞍点，跳出此层循环。若遍历完该列后flag仍为0，则该元素为鞍点，输出该元素的横纵坐标，并且将found置为1。

当found为1时，表明鞍点已找到，此时即可跳出while循环。若在while循环结束后found仍为0，则未找到鞍点，输出NONE。

该循环的特色是当一行中存在不止一个最大值时，可以将每个最大值都依次进行判断，而不会遗漏某个最大值。同时这也是flag=0这一行的定义须在当遍历此行的元素时此行的某一元素等于此行的最大值的if语句之下的原因，这样才能保证每一个最大值元素在判断时flag都重新置为0。

总体代码展示：

n=int(input())
ls=[]
for i in range(n):
    row=list(map(int,input().split()))
    ls.append(row)

found=0
i=0
while i<n:
    max_num=max(ls[i])
    for j in range(n):
        if ls[i][j]==max_num:
            flag=0
            for k in range(n):
                if ls[k][j]<max_num:
                    flag=1
                    break
            if flag==0:
                print(f"{i} {j}")
                found=1
                break
    if found:
        break
    i+=1
                    
if found==0:
    print("NONE")

运行测试：

输入样例1：

4
1 7 4 1
4 8 3 6
1 6 1 2
0 7 8 9

输出样例1：

2 1

运行结果：

输入样例2：

2
1 7
4 1

输出样例2：

NONE

运行结果：

 

额外测试样例：

5
9 8 7 6 5
4 7 9 8 3
1 6 2 6 5
3 7 4 8 9
1 9 8 7 0

该测试样例是为了测试当矩阵的同一行或列有相同最大/小值时是否能正确判断

测试结果：