正定矩阵(用于SVM的Mercer定理)
正定矩阵判定:

定义了一个Cn上的内积。实际上,所有Cn上的内积都可看做由某个正定阵通过此种方式得到。
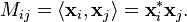
换句话说,M具有A*A的形式,其中A不一定是方阵,但需要是单射的。
-
-
- M左上角1× 1的矩阵
- M左上角2× 2矩阵
- ...
- M自身。
-
对于半正定矩阵来说,相应的条件应改为所有的主子式非负。顺序主子式非负并不能推出矩阵是半正定的。比如以下例子:
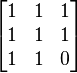
- M = LL * .
其中L * 是L的共轭转置。 T这一分解被称为Cholesky分解。
正定矩阵性质:
对于一般的埃尔米特矩阵,M、N,
当且仅当
。这样可以定义一个在埃尔米特矩阵集合上的偏序关系。类似地,可以定义 M > N。
1.
每个正定阵都是可逆的,它的逆也是正定阵。如果
那么
。
2. 如果 M 是正定阵, r > 0为正实数,那么 rM 也是正定阵。如果 M、N 是正定阵,那么和M + N、乘积 MNM 与 NMN 都是正定的。如果 MN = NM,那么 MN 仍是正定阵。
3. 如果 M = ( m ij ) > 0 那么主对角线上的系数 m ii 为正实数。于是有tr( M ) > 0。此外还有
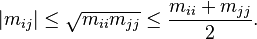
7. 设 M > 0, N 为埃尔米特矩阵。如果( MN + NM > 0),那么
( N > 0)。 8. 如果
为实系数矩阵,则
。 9. 如果 M > 0为实系数矩阵,那么存在δ > 0 使得
,其中 I 为 单位矩阵 。




 本文介绍了正定矩阵的定义及其在SVM中Mercer定理的应用,包括正定矩阵的判定方法、性质及在数学分析中的作用。
本文介绍了正定矩阵的定义及其在SVM中Mercer定理的应用,包括正定矩阵的判定方法、性质及在数学分析中的作用。
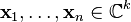
 。如果M是正定阵,可以写作M > 0。这个记法来自
。如果M是正定阵,可以写作M > 0。这个记法来自

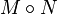
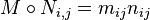

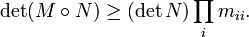
















 810
810

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








