圆锥的表面积

原创于 2025-10-25 09:04:10 发布 · 1.9k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#圆锥 #圆锥体

圆锥体是一种三维几何图形，其底部为圆形，顶部为尖顶（称为顶点）。圆底中心到顶点的距离为圆锥体的高度。圆锥体表面从底部边缘到顶点呈平滑曲线。这种形状常见于冰淇淋蛋筒、交通锥和漏斗等物品。

圆锥体有两种类型的表面积。

锥体的总表面积（TSA）
圆锥的曲面面积（CSA）

在这里，我们将借助解答例题来学习圆锥的表面积，包括总表面积和曲面面积的公式。

下面给出了圆锥体的图示以及计算表面积的公式：

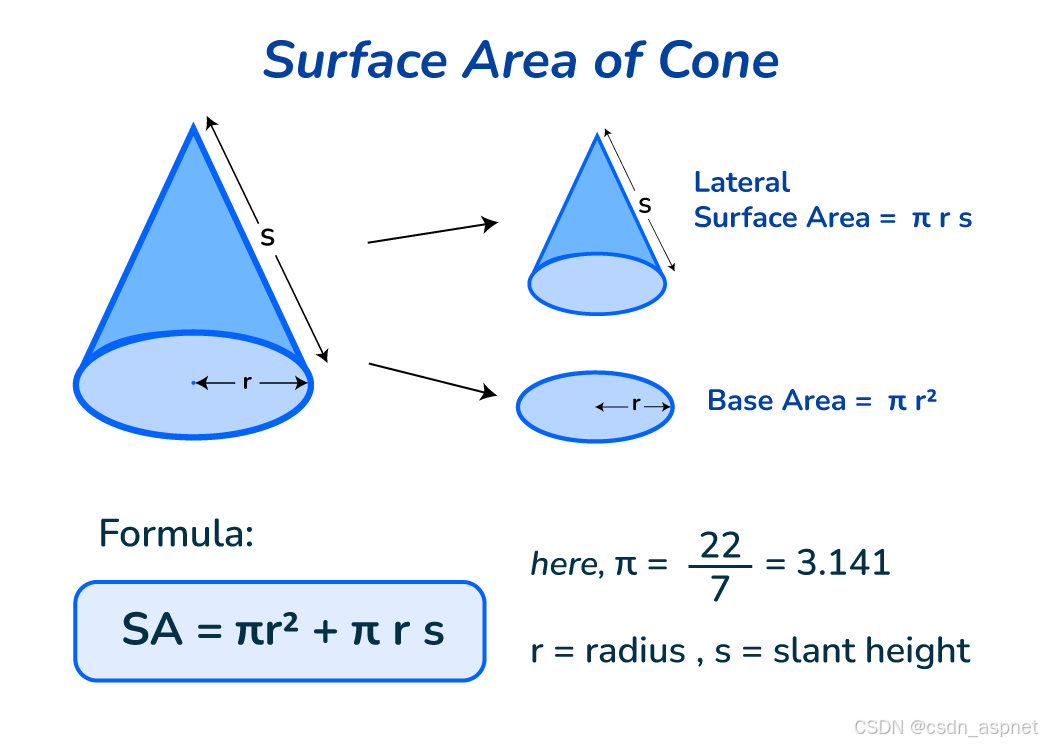
如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。

圆锥表面积公式

如前所述，圆锥的表面积定义为圆锥的边界或表面所占的面积。圆锥的表面积有两种，即曲面面积和总表面积，它们的公式如下。

圆锥体总表面积

圆锥体的总表面积定义为圆锥体在三维空间中所占面积的总和，即曲面面积与圆形底面面积之和。圆锥体的总表面积（TSA）公式如下：

总表面积 = πr(r + l) 平方单位

在哪里，

“ r ” 是圆锥底面半径
“ l ”是圆锥的斜高

圆锥的曲面面积

圆锥的曲面面积定义为圆锥的曲面部分的面积，即圆锥除底面以外的面积，又称为圆锥的侧面积。

圆锥的CSA（曲面面积）公式如下：

曲面面积 (S) = πrl平方单位

在哪里，

“ r ” 是圆锥底面半径
“ l ”是圆锥的斜高

推导：圆锥表面积公式

要观察圆锥表面形成的图形，取一个纸锥，沿其斜高剪开。现在，将 A 和 B 标记为两个端点，将 O 标记为两条线的交点。现在，如果我们打开它，它看起来就像一个圆的扇形。

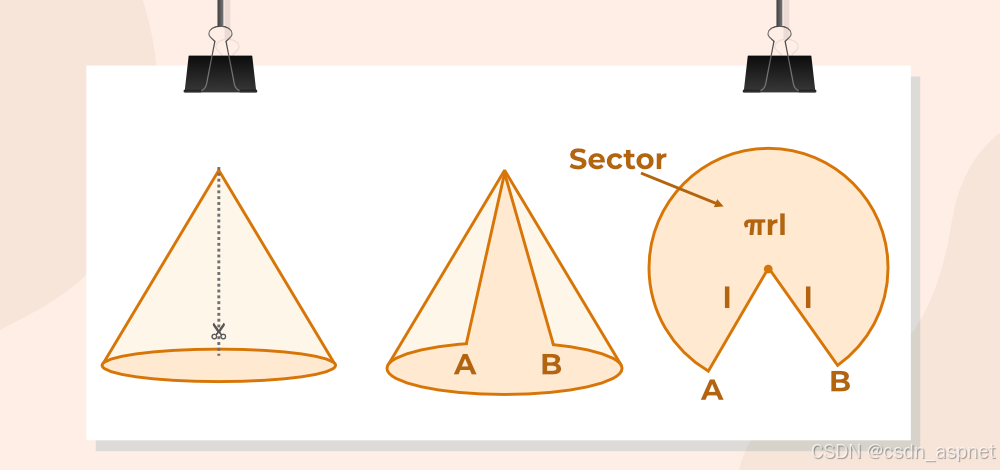
因此，要找到圆锥的曲面面积，我们必须找到扇形的面积。

扇形面积（以弧长表示）= (弧长 × 半径)/2 = ((2πr) × l)/2 = πrl

圆锥的 CSA = πrl 平方单位

圆锥体的总表面积（T）=底面积+曲面面积

由于底面是圆形，所以底面面积为πr^2

⇒ T = πr^2 + πrl = πr(r + l)

圆锥的 TSA = πr (r + l) 平方单位

了解更多：

圆台

斜高圆锥的表面积

考虑圆锥的斜高、高、半径，它们构成一个直角三角形，其中斜高是斜边，底边是底边半径，高是直角三角形的高。

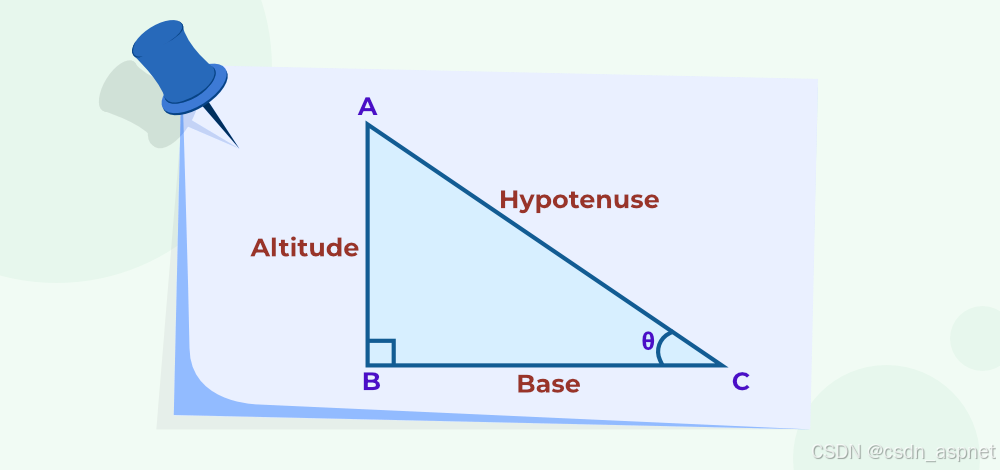
利用勾股定理，我们得到 l^2 = r2 + h2.^2 + h^2

因此，圆锥的斜高 (l) = √(r^2 + h^2 )

因此，通过替换圆锥表面积公式中的斜率值，我们得到

曲面面积 (CSA) = πr√(r^2 + h^2 ) 平方单位

总表面积 (TSA) = πr^2 + πr√(r^2 + h^2 ) 平方单位

圆锥的体积

圆锥的体积是衡量圆锥内部空间大小的量度。它告诉我们圆锥可以容纳多少物质或材料。从数学上讲，圆锥的体积是等底等高的圆柱体体积的三分之一。

体积公式：

体积 = 1/3 (πr^2 h)

圆锥表面积的解答题

问题 1：如果一个圆锥的半径为 15 厘米，斜高为 10 厘米，求其总表面积。（使用 π = 3.14 公式。）

解决方案：

鉴于

圆锥半径（r）= 15厘米
倾斜高度（l）= 10 cm

我们知道，

圆锥体的总表面积 = πr（r + l）平方单位
= (3.14) × 15 × (15 + 10)
= 1,177.5 平方厘米

因此，圆锥体的总表面积为 1,177.5 平方厘米。

问题 2：如果圆锥的半径为 14 个单位，其曲面面积为 1100 平方单位，那么圆锥的高度是多少？（使用 π = 22/7）

解决方案：

鉴于

圆锥半径 (r) = 14 个单位
圆锥的曲面面积 = 1100 平方单位

设圆锥的斜高为“l”，圆锥的高为“h”。

我们知道，

圆锥的曲面面积 = πrl 平方单位
⇒ 1100 = (22/7) × 14 × l
⇒ 44 × l = 1100
⇒ l = 1100/44 = 25 单位

我们知道，

斜高 (l) = √(h^2 + r^2 )
⇒ h = √(l2 - r2)
= √(25^2 - 14^2 ) = √429 = 20.71 个单位

因此，圆锥体的高度为 20.71 个单位。

问题 3：如果圆锥的总表面积为 525 平方厘米，半径为 7 厘米，则确定圆锥的斜高。（使用 π = 22/7）

解决方案：

鉴于

圆锥半径（r）= 7厘米
圆锥体的总表面积 = 525 平方厘米

设圆锥的斜高为“l”

我们知道，

圆锥体的总表面积 = πr（r + l）平方单位
⇒（22/7）×7×（7 + l）= 525
⇒22×（7 + l）= 525
⇒7 + l = 23.86
⇒l = 16.86cm

因此，圆锥的斜高为16.86厘米。

问题4：一个圆锥的半径为9厘米，其曲面面积为407平方厘米。计算圆锥的高。

解决方案：

鉴于

圆锥半径（r）= 9厘米
圆锥体的总表面积 = 407 cm2

设圆锥的斜高为“l”

我们知道，

CSA = πrl平方单位

⇒ (22/7) × 9 × l = 407
⇒ 22 × 198/7 × l = 407
⇒ l = 2849/198
⇒ l = 14.39cm

利用勾股定理求高度 h

l^2 = r^2 + h^2

( 14.39)^2 = 9^2 + h^2

207.09 - 81 = h^2

h = √126.09

h = 11.23 厘米

因此，圆锥体的高度为 11.23 c