多边形的类型

多边形的类型根据各种参数对所有多边形进行分类。众所周知，多边形是仅由边上的直线组成的封闭图形。换句话说，多边形是由二维平面上两条以上的线段构成的封闭图形。“多边形”一词由两个词组成，第一个词是“poly”，表示“许多”，第二个词是“gons”，表示“边”，因此多边形的意思是多条边。多边形由两个部分组成，第一个部分是顶点，第二个部分是边。 

在本文中，我们将讨论多边形的分类，包括凸多边形和凹多边形、简单多边形和复杂多边形、规则多边形和不规则多边形等。因此，让我们从本文开始学习各种类型的多边形。

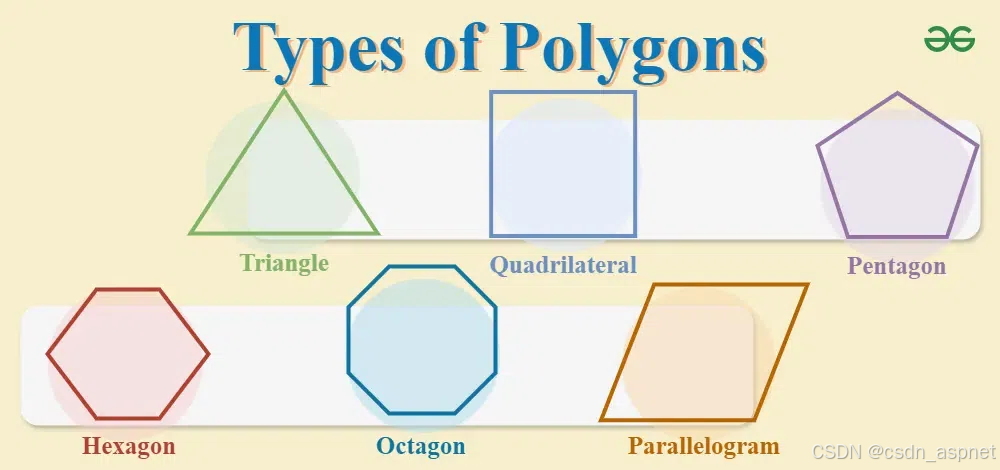
多边形有多少种类型？

多边形可以根据各种不同的参数进行分类，其中一些参数是：

• 基于多边形的边界
• 根据边长
• 基于内角
• 基于侧面

使用多边形公式可以轻松计算多边形的面积。下面让我们根据这些参数详细讨论多边形的类型：

根据多边形边界划分的多边形类型

• 简单多边形
• 复杂多边形

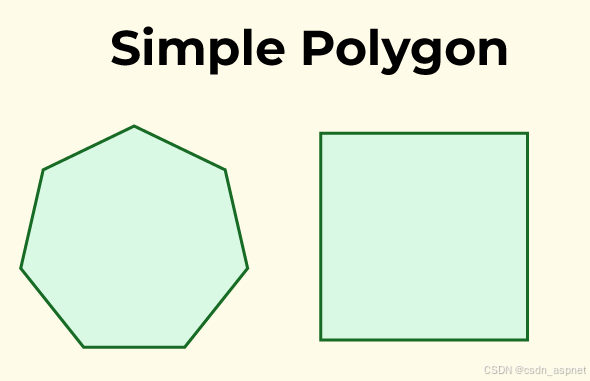
简单多边形

简单多边形是由不相交的线段构成的封闭几何形状。简单来说，边不相交的二维图形被称为简单多边形。常见简单多边形包括三角形、正方形、长方形、五边形、六边形等等。

复杂多边形

复杂多边形是一种二维几何形状，其边由直线段组成，并且可能存在自相交或孔洞。与不自相交的简单多边形不同，复杂多边形的边可以在其边界内相互相交，从而形成更加复杂和不规则的形状。

复杂多边形可以通过组合简单多边形或在简单多边形内添加切口（孔洞）来形成。这些切口会在多边形内创建不属于主边界的区域。与简单多边形相比，自相交和孔洞的加入使得复杂多边形的处理和分析更具挑战性。

根据边长划分的多边形类型

根据边长，多边形可分为以下几种：

• 正多边形
• 不规则多边形

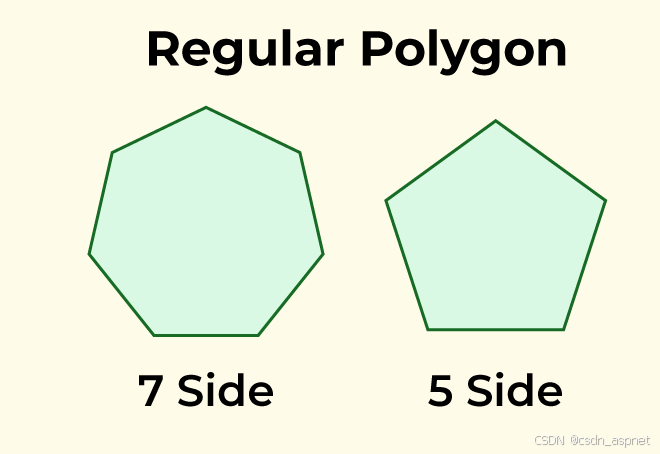
正多边形

如果多边形的所有边和内角都相等，或者多边形是等角多边形和等边多边形，则该多边形被称为正多边形。例如正方形、菱形、等边三角形等。

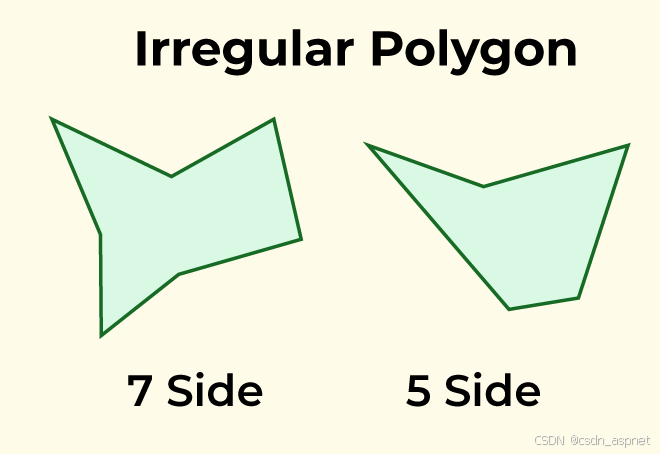
不规则多边形

如果多边形的所有边和内角都不等长，则该多边形被称为不规则多边形。例如不等边三角形、矩形、风筝形等。

基于内角的多边形类型

根据内角的测量，多边形可分为以下几类：

• 凸多边形
• 凹多边形

凸多边形

如果一个多边形的所有内角都严格小于180° ，或者边界上两点之间的线段没有延伸到多边形之外，那么这个多边形就称为凸多边形。

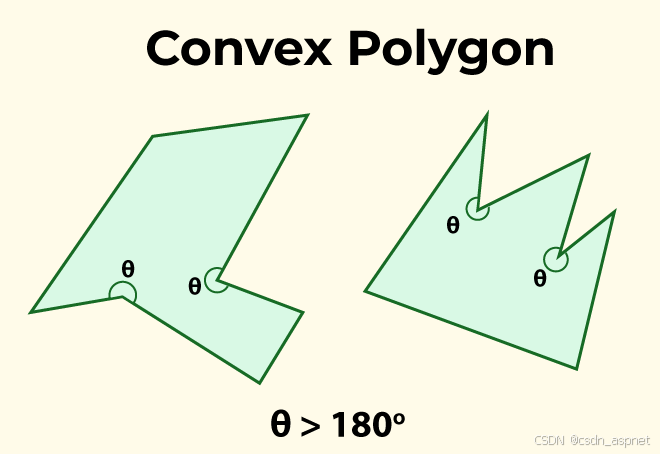
凹多边形

如果多边形的一个或多个内角大于 180°，或者多边形至少包含一个反内角，则该多边形称为凹多边形。凹多边形至少有四条边。

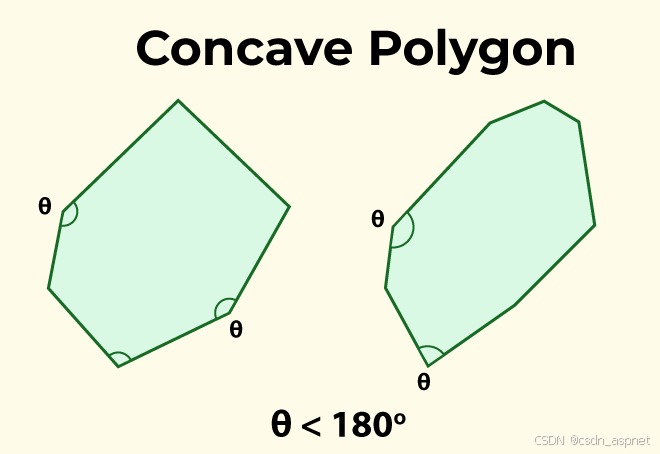
基于边的多边形类型

多边形根据其边数或顶点数进行分类。以下是一些多边形：

• 三角形
• 四边形
• 五角大楼
• 六边形
• 很快 。 。 。

下表给出了所有这些多边形：

多边形	形状	边数	对角线数量	顶点数	内角	外角
三角形		3	0	3	60°	120°
四边形		4	2	4	90°	90°
五角大楼		5	5	5	108°	72°
六边形		6	9	6	120°	60°
七边形		7	14	7	128.571°	51.429°
八角形		8	20	8	135°	45°
九纳贡		9	二十七	9	140°	40°
十边形		10	三十五	10	144°	36°
十一边形		11	四十四	11	147.273°	32.727°
十二边形		12	54	12	150°	30°
十三边形		十三	65	十三	158.308°	27.692°
十四边形		14	77	14	154.286°	25.714°
十五边形		15	90	15	156°	24°

三角形（3边形）

三角形是一种多边形，它由三条线段相交而成，因此三角形有3个顶点、3条边和3个角。根据边和角的不同，三角形又分为不同的类型。  

三角形的一些性质：

• 三角形面积：1/2×底×高
• 在三角形中，所有内角的总和为 180 o。
• 最大角所对的边就是三角形的最长边。
• 三角形的周长等于三角形三边的长度之和。

类型：基于侧面

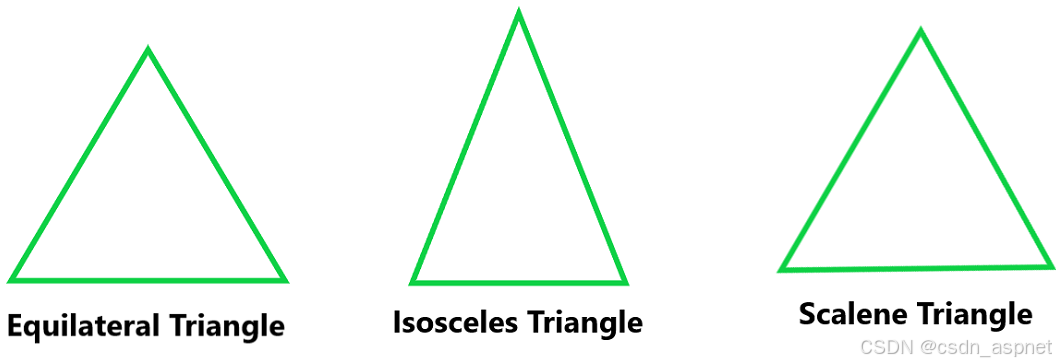
• 等边三角形：如果三角形的所有边都相等且角也相等，则这种类型的三角形称为等边三角形。
• 等腰三角形：如果任何三角形有两条边相等，并且与相等边相对的角也相等，那么这种类型的三角形称为等腰三角形。
• 不等边三角形：如果三角形的三条边都不相等，则这种类型的三角形称为不等边三角形。

​

类型：基于角度

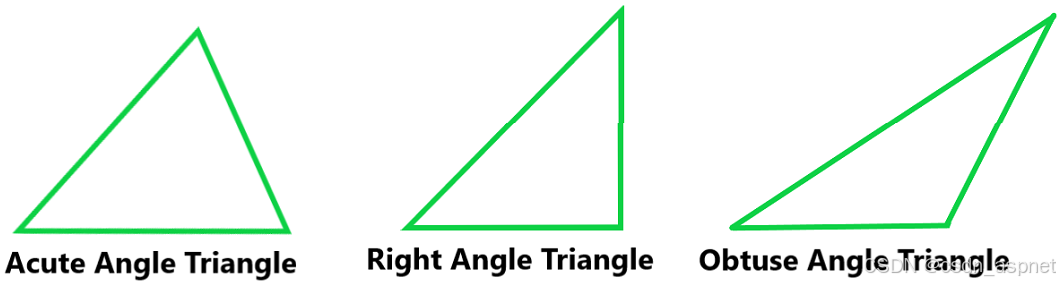
• 锐角三角形：角度小于 90° 的三角形称为锐角三角形。
• 直角三角形：如果三角形的三个角中任意一个等于 90°，则这种三角形称为直角三角形。
• 钝角三角形：如果三角形的任何一个角大于 90°，则这种类型的三角形称为钝角三角形。

​

四边形（4边形） 

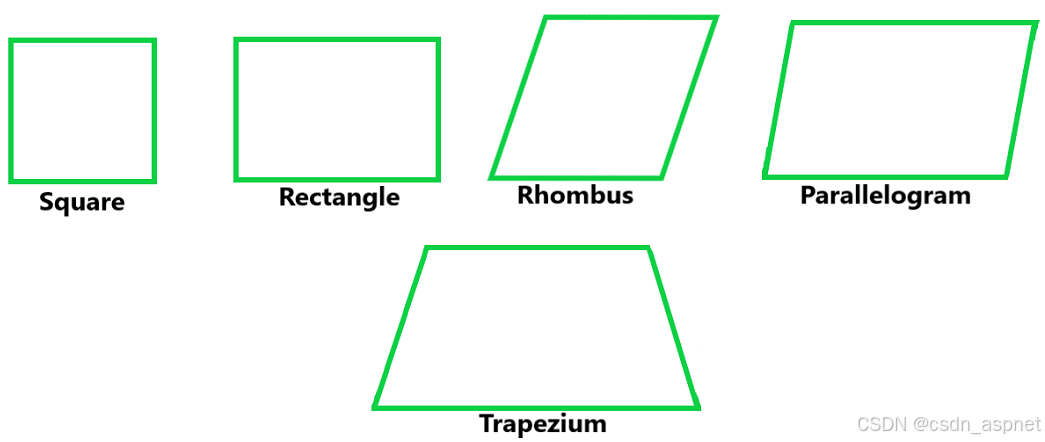
四边形就是至少有四条边的多边形。多边形是由四条线段组成的，这些线段在顶点处相交，形成四个或更多个角。四边形的例子有正方形、长方形、平行四边形、菱形、梯形。

四边形的一些性质：

• 它有四面。
• 它有四个顶点。
• 在四边形中，所有内角的总和是 360 °。

​

除了三角形和四边形之外，还有其他多边形，但它们在现实生活中用处不大。

如，

• 多面体
• 多边形的对角线

多边形类型的示例问题

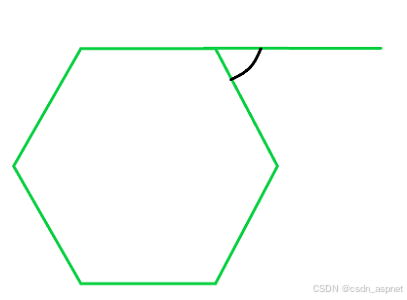
问题 1. 求正六边形的外角。

解决方案： 

我们知道，六边形有 6 条边，因此

外角 = 360 ° / n = 360 ° / 6

外角 = 60°

​

问题 2. 求正五边形的内角。

解决方案： 

我们知道五边形有 5 条边，因此

外角 = 360 °/ 5 = 72 °

内角 = 180 ° - 72 ° = 108 °​​​​​​​

问题 3. 求正十边形的每个内角。

解决方案： 

我们知道，十边形有十条边。

使用角和公式， 

我们知道，

S = (n − 2) × 180°

这里，n = 10

所以，

十边形内角和 = (10 − 2) × 180°

= 8 × 180° = 1440°

我们知道正十边形的所有内角都相等， 

因此，正十边形每个内角的度数=内角和/边数

内角 = 1440 / 10 = 144°

因此，十边形的内角和为 1440°，每个内角为 144°。  

问题 4. 找出给定图中 x 的值：

​

解决方案：

我们知道四边形的角和 = 360°

所以，55° + 124° + 70° + x = 360°

249°+ x = 360°

x = 111°

问题 5. 找出给定图中 x 的值：

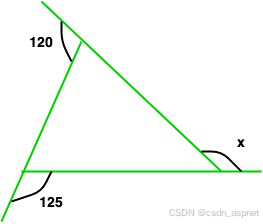
解决方案：

我们知道外角和 = 360°

所以，120 ° + 125° + x = 360 °

245°+ x = 360°

x = 360°- 245°

x = 115°

参考：Types of Polygons - GeeksforGeeks 

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。