描述函数法(Describing Function Analysis)
描述函数法依然属于线性系统中频率响应的扩展应用,优点就是比较容易设计,缺点也是显然的,理论性不足,比较依赖于假设,不是万能的,也不是很准确,但是工程价值还是有的。
适用于:
- 只有一个非线性元件(很多时候把非线性合并到一起)
- 非线性时不变
- 只考虑基波分量
具体需要一些些傅里叶变换,再忽略高次谐波…blablabla。
例1.确定下图是否存在一个极限环,若存在,频率幅值是多少。
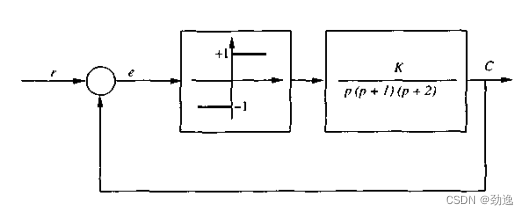
开关效应的描述函数为:
N=4/(πA)
N = 4/(\pi A)
N=4/(πA)
那么对于jωj\omegajω的输入而言,有G(jω)=−1/NG(j\omega) = -1/NG(jω)=−1/N,ω=2Hz\omega = \sqrt{2}Hzω=2Hz(角频率)时,有极限环。
例2.如下系统是否存在极限环,G(p)=−5p/(p2+p+25)G(p) = -5p/(p^2+p+25)G(p)=−5p/(p2+p+25)
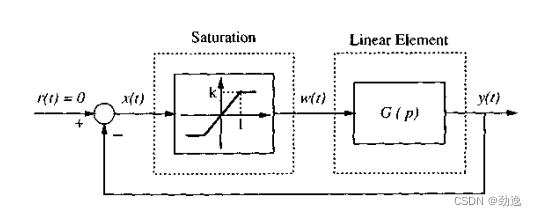
算一下可以发现ω=5Hz\omega = 5Hzω=5Hz(角频率)时,有极限环。由于饱和特性不会影响频率特性,无相角特性,所以振荡频率很准确,不会因为扰动和初值而改变。也可以解释为若无饱和环节的闭环系统本来就是不稳定的,系统逐渐发散,未饱和不稳定,饱和以后也不能停留在饱和值,但是饱和环节制约了系统进一步增长,所以极限环振荡,下图为简单仿真结果。
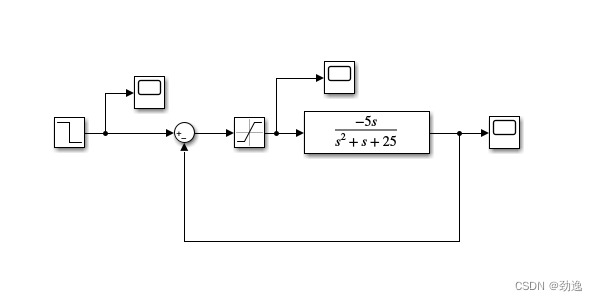
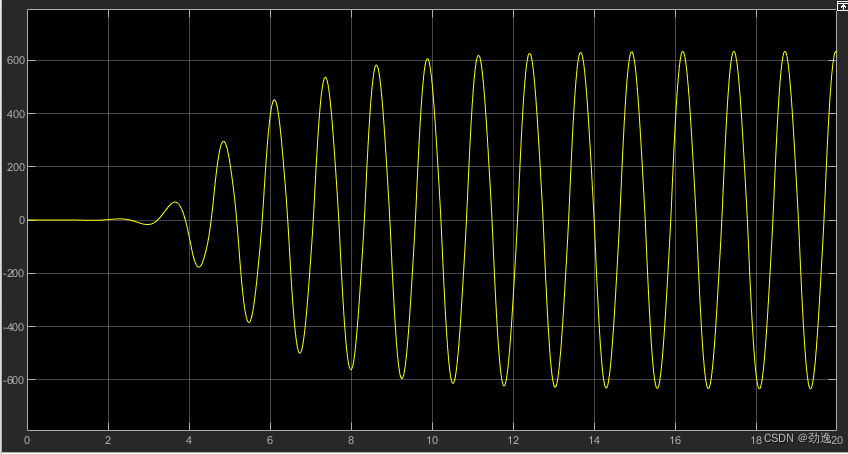
 描述函数法:非线性系统的频率响应分析与极限环形成
描述函数法:非线性系统的频率响应分析与极限环形成




















 7138
7138










