因子分析（3）- 都是坑！这么简单的Alpha计算，竟然错了？！

最新推荐文章于 2025-08-08 01:46:27 发布
原创 最新推荐文章于 2025-08-08 01:46:27 发布 · 1.8k 阅读 · 20 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#量化交易 #quant #因子分析 #Alphalens

本文解释了在使用Alphalens进行因子分析时，如何理解alpha和beta的计算原理，以及在单边策略中权重调整的重要性。作者指出默认情况下，Alphalens的权重计算可能导致误解，特别是对于换手率等不能同时做多做空的因子，需将其转换为与收益率正相关的指标。

我们继续 Alphalens 因子分析报告的解读。在过去的两篇笔记中，我们都提到，运用 Alphalens 进行因子分析步骤很简单，但是如果不了解它背后的机制与逻辑，很容易得到似是而非的结论。这篇笔记一开始，我们就会再介绍一个常见错误。

Alphalens 提供了alpha和beta分析。方法是factor_alpha_beta：

from alphalens.performance import factor_alpha_beta

alpha, beta = factor_alpha_beta(factor_data)

我们将得到以下输出：

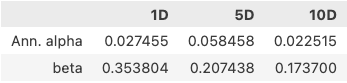
看上去很完美。

这个结果表明，该因子的年化alpha是2.7%，风险暴露为35%，一定程度上受到市场影响。我们按照 Alphalens 的要求，通过 get_clean_factor_and_forward_returns 方法获得了 factor_data, 然后用它来计算 alpha 和 beta。过程简单明了，似乎不可能出任何错误。

但实际上，如此得到的 alpha 和 beta，在我们这个示例中并没有任何意义。

在这里插入图片描述

在Alphalens中，alpha和beta是通过因子组合收益对市场组合收益的最小二乘回归（OLS）来求得的。

!!! info Alphalens在这里借用了statsmodels中的OLS方法。

其中，市场组合的收益是对各标的收益的简单平均。假设我们的组合共有4个标的，某一日它们各自的收益分别为:
0.01189, 0.01102, -0.01241和-0.01898，则当日市场组合的收益为

(0.01189+0.01102−0.01241−0.01898)/4=−0.00212 (0.01189 + 0.01102 -0.01241 -0.01898)/4= -0.00212 (0.01189

最低0.47元/天 解锁文章
Super-Resolution by POCS-SIFT 算法深度解析！
**My Coding Family**
12-25 479
🏆本文收录于 《全栈 Bug 调优（实战版）》 专栏。专栏聚焦真实项目中的各类疑难 Bug，从成因剖析 → 排查路径 → 解决方案 → 预防优化全链路拆解，形成一套可复用、可沉淀的实战知识体系。无论你是初入职场的开发者，还是负责复杂项目的资深工程师，都可以在这里构建一套属于自己的「问题诊断与性能调优」方法论，助你稳步进阶、放大技术价值 。
使用InVEST模型进行SDR模块计算，遇到了输出结果中包含许多空值（null values），如何解决？
**My Coding Family**
04-29 996
🏆本文收录于 《全栈 Bug 调优（实战版）》 专栏。专栏聚焦真实项目中的各类疑难 Bug，从成因剖析 → 排查路径 → 解决方案 → 预防优化全链路拆解，形成一套可复用、可沉淀的实战知识体系。无论你是初入职场的开发者，还是负责复杂项目的资深工程师，都可以在这里构建一套属于自己的「问题诊断与性能调优」方法论，助你稳步进阶、放大技术价值 。
量化交易-单因子分析-alphalens
xu624735206的博客
02-22 2535
alphalens单因子分析
Alphalens使用方法细节判断
qq_26742269的博客
11-26 2456
Alphalens学习
金融学习之三——晕头转向的alphalens
ryo007gnnu的博客
02-23 4868
alphalens分析是一个进行单因子分析的开源项目。alphalens需要的数据有自己要求的格式，因此整个过程就分为两个部分：（a）处理数据，形成所需的格式（b）计算并理解数据的结果。 下午跑了一遍前文书中提到的alphalens单因子有效性分析，程序是跑完了，可结果还有待看懂，大概的过程如下： （1）获取数据，进行初步处理 import tushare as ts ts.set_token('*********************************') pro=ts.pro_api() dat
Alphalens使用过程及心得
热门推荐
WenbinYao&YouweiHu
08-04 2万+
1、说明 最近，做因子回测时用到了Alphalens，这里简单介绍下alphalens的使用，但是由于有一篇东北证券的研报写得还算清楚了，而且由于是开源的，大家可以直接看源代码，那篇研报基本上也就是翻译了一下源代码的介绍而已，在这里的话，建议大家可以看一眼研报，然后使用前，还是看一下源码，可能是因为后来alphalens又更新了，那篇研报上有一些函数的参数有错误。 本篇博文会简单介绍下alphal...
alphalens的单因子测试
07-30
本课程正对股票alpha策略的入门者和初学者，介绍了整个alpha策略（多因子）的体系和投资哲学，然后重点介绍了单因子测试的核心点。因子测试部分包括示例因子的计算、因子的预处理（包括去极值化、标准化、中性化）、基于alphalens的因子测试。最后对因子测试的结果进行详细的分析，并从实际意义上说明，怎么样的测试结果是一个好的因子。
计算个股CAPM模型和Fama-French五因子模型（by Stata16MP）
m0_46441797的博客
04-25 1万+
实验要求： 选择5只在上交所上市交易的股票的月度收益率（近10年）； 对每只股票估计CAPM模型和Fama-French五因子模型，解释估计量的金融含义； 从两个模型的估计结果，你能得到哪些结论？ step1：获得实验数据 method1：通过url下载（网易财经提供的数据） 浦发银行 http://quotes.money.163.com/service/chddata.html?code=0600000&end=20201231&fields=TCLOSE;HIGH;LOW;
量化价值投资因子投资：你应该知道的那些事
AI天才研究院
08-08 651
这就是因子投资要解决的问题。
基于alphalens对qlib的alpha158做单因子分析
weixin_38175458的博客
09-01 3671
这里本质大家要想清楚，即便你的策略的确不包含“未来函数”，没有错误，但很有可能包括了”隐性“未来函数，比如2016年以来，价值因子明显有收益，像消费行业起飞，若你的策略使用的是价值因子，那超额收益一定不错，但这个一定可以持久的嘛？4、qlib肯定有不完善的地方，但目前来看，还是值得坚守，自己造一个平台，一开始看似爽，但后面到了大数据，算法阶段，该踩的坑一个不少，都得踩，毕竟微软还是有它的实力在，没有必要从头造轮子。2、对于量化而言，数据预处理都差不多，一则就找更好的数据源，二则找更好的特征。...
量化投资单因子回测神器 — Alphalens
Python实用宝典网
11-23 4075
量化投资往期推荐量化投资实战教程(1)—基于backtrader的简单买入卖出策略量化投资实战教程(2)—MACD策略(+26.9%)量化投资实战教程(3) —A股回测MACD策略Pyth...
当 Alphalens 遇上 DolphinDB：单因子分析利器再升级
DolphinDB智臾科技
06-19 2025
Alphalens 是 Quantopian 用 Python 开发的一个因子分析（评价）工具包，使用 Alphalens，我们可以对单因子的有效性进行全面分析。目前，我们用 DolphinDB 的脚本语言实现了 Alphalens 因子分析模块。阅读原文了解 DolphinDB Alphalens 因子分析模组实战手册！
【Alphalens】使用Alphalens配合Akshare进行双均线因子分析，附源码及常见问题
airyv的博客
04-15 1707
Alphalens 是非常著名的一个python因子分析库。但是该库由于目前已经不怎么维护，问题非常多。。由于该库的demo都是基于国外雅虎财经的接口yfinance。如果使用国内的akshare配合使用会出现一下问题。需要对Alphalens接口非常熟悉。建议阅读其原始接口的注释，特别是get_clean_factor_and_forward_returns方法。
alphalens框架使用说明
小白兔奶糖
12-19 2476
alphalens框架使用说明
alphalens 事件_alphalens教程1--整理好你的数据
weixin_35871890的博客
12-24 792
很久以前研究过这个，周末下大雨，整理一下子IDE里面的工程文件，发现了当时的测试demo，于是决定再来感受一下。alphalens是quantopian下的三大quant利器这里，剩下两个是大名鼎鼎的zipline和pyfolio。alphalens是用于因子回测的，使用很方便，但是，最大的一个特点就是，函数的名称真是长啊！安装就不说了，似乎pip就可以了。万事开头难，中间也难，结尾更难。很多事确...
qlib因子分析之alphalens源码解读
weixin_38175458的博客
09-02 1881
传统动量模型，比如20日动量>0.02就买入，小于0就卖出，和MACD>0一样，在大牛市非常好，震荡市让你怀疑人生，关键是你不知道当前是什么趋势。量化投资本质上就是“找因子”，技术分析里可以量化的部分都是因子，因子进入模型不是hard-code的，而是以概率的形式，这就存在可以学习和优化的空间。收益分析看起来有点类似“回测”，按因子高低买卖，看回测结果——结果都不错，但似乎没什么用，关键还看“信息分析”。有点像体验里验血、尿，B超等，给出一系列量化指标，再结合你的表述，症状，有经验的医生就可以给出结果。
Quantopian单因子分析工具：Alphalens
卤蛋爱编程
11-22 2962
Quantopian是国外著名的量化交易平台，早期聚宽就是仿照这个网站开发的，算是这类平台的鼻祖了，可惜Quantopian最近刚宣布要停止运营了。Quantopian开发了许多优秀的开源项目，其中比较著名的有zipline、pyfolio和alphalens，zipline是事件驱动的回测引擎，Alphalens与Zipline开源回溯测试库以及Pyfolio配合使用，Pyfolio提供金融投资组合的绩效和风险分析。 Alphalens主要功能是alpha因子的相关性统计数据和图表展示，包括： Retu
Alphalens笔记
winter_python的博客
11-27 4180
数据预处理 factor_data = utils.get_clean_factor_and_forward_returns(factor_df, price_df, quantiles=5, bins=None,periods=(1, 5, 10, 20), max_loss=0.5) tears.py @plotting.customize def create_full_tear_shee...
如何计算OBV(能量潮)指标并应用于量价分析？
最新发布
12-22
<think>我们已知OBV（On-Balance Volume）的计算方法，并且有多个引用资料作为参考。根据引用[3]，OBV的计算步骤如下： 1. 计算每日价格变化：使用收盘价的差分 2. 判断涨跌方向：如果当日收盘价上涨，则方向为1；下跌则为-1；持平为0 3. 计算OBV：将方向与成交量相乘，然后累加 但是，引用[1]提到OBV的理论基础是成交量的变化先于价格变动，因此我们还需要考虑如何将OBV应用于量价分析。 另外，引用[2]提到TA-Lib中也有交易量指标，但OBV在TA-Lib中是一个独立的函数，因此我们也可以使用TA-Lib来计算OBV。 根据用户的需求，我们将提供两种方法计算OBV： 方法一：使用Pandas手动计算（如引用[3]所示） 方法二：使用TA-Lib库计算（更高效且标准） 然后，我们将展示如何将OBV指标应用于量价分析，例如： - 价格与OBV的背离分析 - OBV突破其移动平均线作为交易信号 步骤： 1. 计算OBV 2. 可视化价格和OBV 3. 分析OBV与价格的关系（背离等） 4. 结合其他指标（如OBV的移动平均线）产生交易信号 注意：在计算OBV时，初始值通常设为0，然后逐日累加。 我们按照以下结构组织代码： a. 导入必要的库（pandas, numpy, matplotlib, talib等） b. 获取股票数据（这里使用tushare示例，但用户可替换为其他数据源） c. 计算OBV（两种方法） d. 可视化 e. 量价分析示例（背离分析等） f. 生成交易信号（例如：当价格创新低而OBV未创新低时，视为底背离，可能预示反弹） 注意：由于引用[3]指出“你可能遇到的坑”，比如当价格不变时方向为0，这样成交量不计算在内。这一点在实现时要注意。 下面开始编写代码示例： </think> ### OBV（能量潮）指标计算与量价分析实现 根据引用资料[^1][^3]，OBV指标通过成交量变化衡量市场买卖力量，其计算原理如下： #### 1. OBV计算公式 OBV的计算基于价格方向和成交量： $$ \text{OBV}_t = \begin{cases} \text{OBV}_{t-1} + \text{Volume}_t & \text{if } \text{Close}_t > \text{Close}_{t-1} \\ \text{OBV}_{t-1} - \text{Volume}_t & \text{if } \text{Close}_t < \text{Close}_{t-1} \\ \text{OBV}_{t-1} & \text{if } \text{Close}_t = \text{Close}_{t-1} \end{cases} $$ #### 2. Python实现方法 使用Pandas计算OBV指标（引用）： ```python import pandas as pd import matplotlib.pyplot as plt import yfinance as yf # 需要安装: pip install yfinance # 获取股票数据 def get_stock_data(symbol, start_date, end_date): data = yf.download(symbol, start=start_date, end=end_date) return data # 计算OBV指标 def calculate_obv(data): """计算OBV能量潮指标""" # 计算价格变化 data[&#39;Price_Change&#39;] = data[&#39;Close&#39;].diff() # 确定方向因子: 上涨为+1, 下跌为-1, 平盘为0 data[&#39;Direction&#39;] = data[&#39;Price_Change&#39;].apply( lambda x: 1 if x > 0 else (-1 if x < 0 else 0) ) # 计算OBV (注意：成交量单位需统一，这里使用股数) data[&#39;OBV&#39;] = (data[&#39;Direction&#39;] * data[&#39;Volume&#39;]).cumsum() return data # 示例使用 if __name__ == "__main__": # 获取苹果公司股票数据 aapl = get_stock_data(&#39;AAPL&#39;, &#39;2023-01-01&#39;, &#39;2023-12-31&#39;) # 计算OBV aapl = calculate_obv(aapl) # 可视化 fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8), sharex=True) # 价格图表 aapl[&#39;Close&#39;].plot(ax=ax1, title=&#39;AAPL收盘价&#39;, color=&#39;blue&#39;) ax1.set_ylabel(&#39;价格($)&#39;) # OBV图表 aapl[&#39;OBV&#39;].plot(ax=ax2, title=&#39;OBV能量潮&#39;, color=&#39;green&#39;) ax2.axhline(y=0, color=&#39;gray&#39;, linestyle=&#39;--&#39;, alpha=0.7) ax2.set_ylabel(&#39;OBV值&#39;) plt.tight_layout() plt.show() ``` #### 3. 量价分析应用 OBV指标可用于以下量价分析场景： 1. **价格-成交量背离检测**（引用[^1]） ```python def detect_divergence(data, window=14): """检测价格与OBV的背离""" data[&#39;Price_High&#39;] = data[&#39;Close&#39;].rolling(window).max() data[&#39;OBV_High&#39;] = data[&#39;OBV&#39;].rolling(window).max() # 顶背离: 价格新高但OBV未创新高 top_divergence = (data[&#39;Close&#39;] == data[&#39;Price_High&#39;]) & (data[&#39;OBV&#39;] < data[&#39;OBV_High&#39;]) # 底背离: 价格新低但OBV未创新低 data[&#39;Price_Low&#39;] = data[&#39;Close&#39;].rolling(window).min() data[&#39;OBV_Low&#39;] = data[&#39;OBV&#39;].rolling(window).min() bottom_divergence = (data[&#39;Close&#39;] == data[&#39;Price_Low&#39;]) & (data[&#39;OBV&#39;] > data[&#39;OBV_Low&#39;]) return top_divergence, bottom_divergence ``` 2. **OBV趋势确认** - OBV突破移动平均线作为交易信号： ```python def obv_trading_signal(data, ma_period=20): """生成OBV交易信号""" data[&#39;OBV_MA&#39;] = data[&#39;OBV&#39;].rolling(ma_period).mean() # 买入信号: OBV上穿均线 data[&#39;Buy_Signal&#39;] = (data[&#39;OBV&#39;] > data[&#39;OBV_MA&#39;]) & (data[&#39;OBV&#39;].shift(1) <= data[&#39;OBV_MA&#39;].shift(1)) # 卖出信号: OBV下穿均线 data[&#39;Sell_Signal&#39;] = (data[&#39;OBV&#39;] < data[&#39;OBV_MA&#39;]) & (data[&#39;OBV&#39;].shift(1) >= data[&#39;OBV_MA&#39;].shift(1)) return data ``` 3. **量能潮强度分析** ```python def volume_strength_analysis(data): """量能强度分析""" # 计算OBV变化率 data[&#39;OBV_Change&#39;] = data[&#39;OBV&#39;].pct_change() * 100 # 量价同步指标 data[&#39;Price_OBV_Ratio&#39;] = data[&#39;Close&#39;].pct_change() / (data[&#39;OBV_Change&#39;] + 1e-5) # 量能异常波动 data[&#39;Volume_Anomaly&#39;] = data[&#39;Volume&#39;] > 2 * data[&#39;Volume&#39;].rolling(20).mean() return data ``` #### 4. 注意事项（引用[^3]） 1. **单位一致性**：确保成交量单位统一（如都用股数或手数） 2. **数据质量**：处理缺失值和异常值 ```python data.dropna(inplace=True) # 删除缺失值 ``` 3. **初始值处理**：OBV计算从0开始累积 4. **平盘处理**：当价格不变时，OBV保持不变 #### 5. TA-Lib实现（引用[^2]） 使用专业库计算更高效： ```python import talib # TA-Lib计算OBV aapl[&#39;OBV_TA&#39;] = talib.OBV(aapl[&#39;Close&#39;], aapl[&#39;Volume&#39;]) # 比较两种方法结果 (aapl[&#39;OBV&#39;] - aapl[&#39;OBV_TA&#39;]).plot(title=&#39;Pandas与TA-Lib计算结果差异&#39;) ``` ### 应用案例：苹果股票量价分析 ```python # 应用前述函数 aapl = obv_trading_signal(aapl) aapl = volume_strength_analysis(aapl) top_div, bottom_div = detect_divergence(aapl) # 标记背离点 aapl.loc[top_div, &#39;Top_Divergence&#39;] = aapl[&#39;Close&#39;][top_div] aapl.loc[bottom_div, &#39;Bottom_Divergence&#39;] = aapl[&#39;Close&#39;][bottom_div] # 可视化分析结果 aapl[[&#39;Close&#39;, &#39;OBV&#39;, &#39;Top_Divergence&#39;, &#39;Bottom_Divergence&#39;]].plot( secondary_y=&#39;OBV&#39;, figsize=(14, 8), title=&#39;AAPL量价背离分析&#39; ) ``` 通过OBV指标分析，可识别： 1. **量价背离**：预示趋势反转 2. **量能突破**：确认趋势强度 3. **异常放量**：识别关键转折点
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

量化风云

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值