B4260 [GESP202503 二级] 时间跨越

最新推荐文章于 2025-12-19 16:34:09 发布

原创最新推荐文章于 2025-12-19 16:34:09 发布 · 450 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #解题思路 #GESP历史真题

B4260 [GESP202503 二级] 时间跨越 - 洛谷

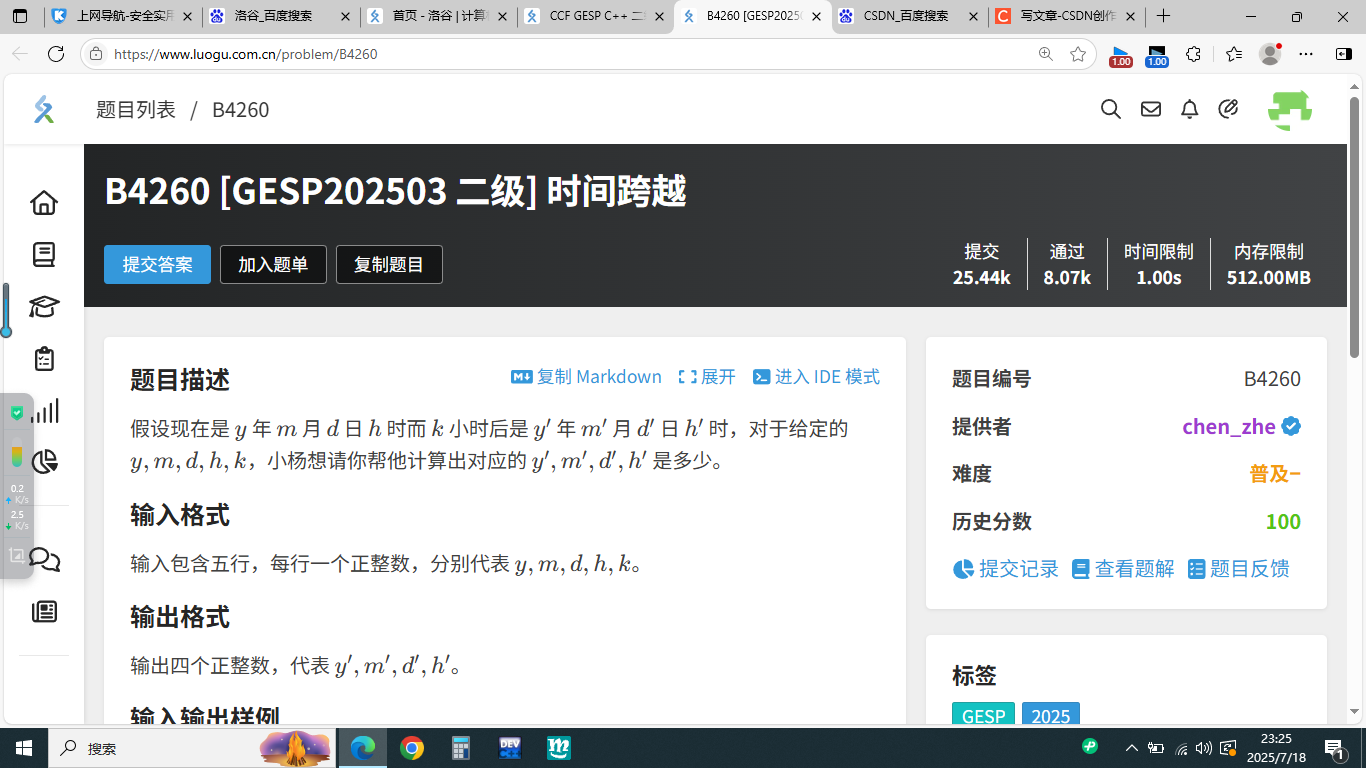
这一题只要用多分支结构和并列的if就行了，程序如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

int main() {
   LL y, m, d, h, k, cnt = 0, day = 0;
   cin >> y >> m >> d >> h >> k;
   if (m == 1 || m == 3 || m == 5 || m == 7 || m == 8 || m == 10 || m == 12) {
       day = 31;
   } else if (m == 4 || m == 6 || m == 9 || m == 11) {
       day = 30;
   } else if (m == 2) {
       if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
           day = 29;
       } else {
           day = 28;
       }
   }
   cnt = h + k;
   if (cnt >= 24) {
       cnt -= 24;
       d += 1;
   }
   if (d > day) {
       d -= day;
       m += 1;
   }
   if (m > 12) {
       m = 1;
       y += 1;
   }
   cout << y << ' ' << m << ' ' << d << ' ' << cnt;
   return 0;
}