现代卷积神经网络

LeNet

总体来看，LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成;

• 全连接层密集块：由三个全连接层组成。

代码

import torch
from torch import nn
from d2l import torch as d2l

class Reshape(torch.nn.Module):
    def forward(self, x):
        return x.view(-1, 1, 28, 28)

#LeNet网络
net = torch.nn.Sequential(Reshape(), nn.Conv2d(1, 6, kernel_size=5,
                                               padding=2), nn.Sigmoid(),
                          nn.AvgPool2d(kernel_size=2, stride=2),
                          nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
                          nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
                          nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
                          nn.Linear(120, 84), nn.Sigmoid(), nn.Linear(84, 10))

# 输出模型流程
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape: \t', X.shape)


# LeNet在Fashion-MNIST数据集上的表现

#加载数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

#使用GPU进行运算，修改评估函数
def evaluate_accuracy_gpu(net, data_iter, device=None):  
    """使用GPU计算模型在数据集上的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval()
        if not device:
            device = next(iter(net.parameters())).device
    metric = d2l.Accumulator(2)
    for X, y in data_iter:
        if isinstance(X, list):
            X = [x.to(device) for x in X]
        else:
            X = X.to(device)
        y = y.to(device)
        metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

#训练函数
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)。"""

    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight) #初始化权重w
            """
            Xavier初始化的实现
            权重的赋值会按照均匀分布或正态分布
            Xavier初始化的目的 
            控制方差：它旨在维持各层激活和反向传播梯度的方差。
                            通过这样做，它有助于防止在深度网络中常见的梯度消失或梯度爆炸问题。
            有效训练：适当的初始化可以导致训练更快收敛，
                            因为它确保梯度不会太快消失或爆炸。
            """

    #net模型使用init_weights函数
    net.apply(init_weights)
    print('training on', device)
    
    #将模型移动到特定设备device上
    net.to(device)

    #采用SGD（随机梯度下降）更新模型参数
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()

    #图形化
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    
    for epoch in range(num_epochs):
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

# 训练并评估
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

AlexNet

1. AlexNet是更大更深的LeNet

2. 新引进了Dropout，ReLU激活函数，最大池化层，数据增强

代码

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2), nn.Flatten(),
    nn.Linear(6400, 4096), nn.ReLU(), nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(p=0.5),
    nn.Linear(4096, 10))

#观察每一层的输出
X = torch.randn(1, 1, 224, 224)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'Output shape:\t', X.shape)

# 加载数据集
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

# 训练
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

VGG

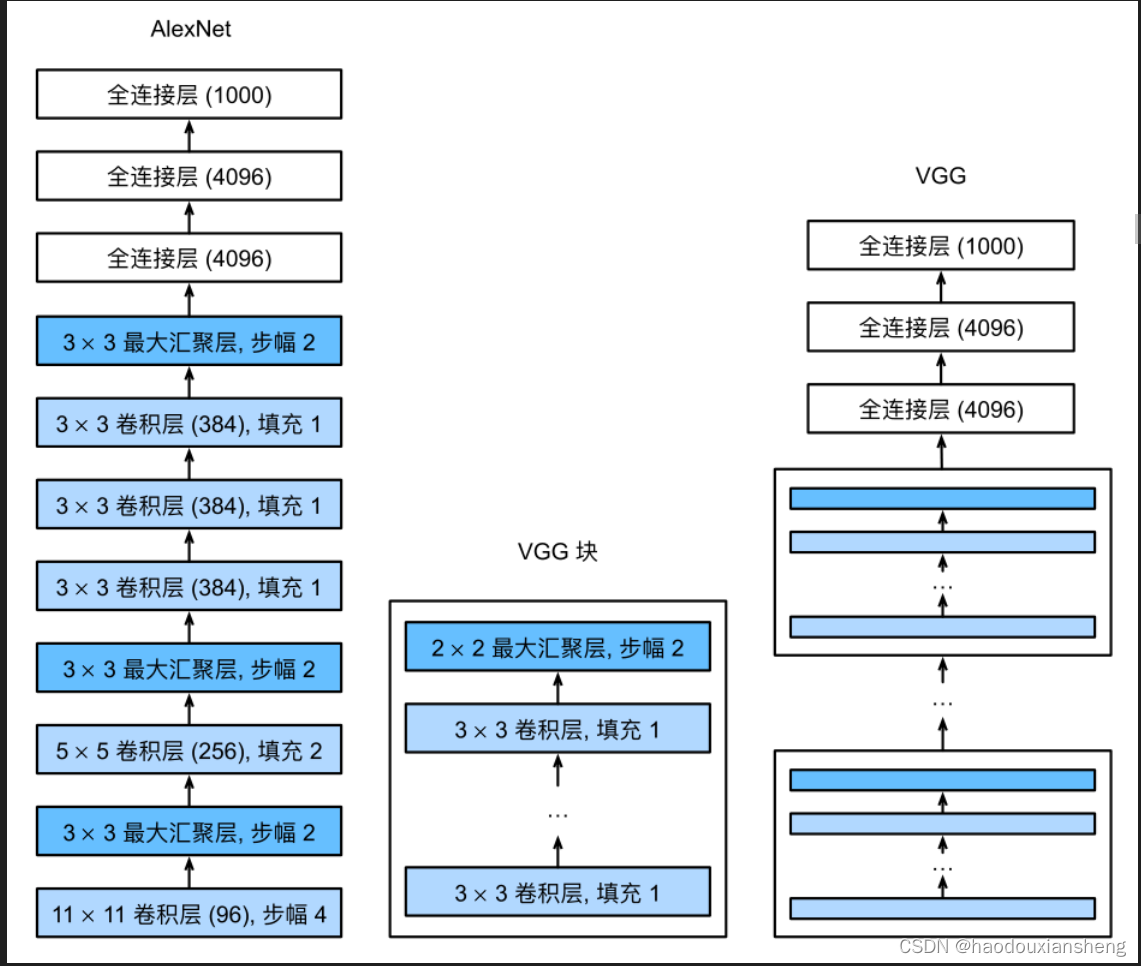
1.VGG使用可重复使用的卷积块来构建深度卷积神经网络

(将AlexNet的 卷积层-池化层 模块化，整合成一个VGG块，通过调用VGG块实现该过程的重复进行)

2.不同的卷积块个数和超参数可以得到不同复杂度的变种

代码

import torch
from torch import nn
from d2l import torch as d2l

#VGG块
#num_convs 卷积层个数
def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        #卷积层
        layers.append(
            nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        #激活函数
        layers.append(nn.ReLU())
        in_channels = out_channels

    #池化层
    layers.append(nn.MaxPool2d(kernel_size=2, stride=2))
    return nn.Sequential(*layers)

#VGG网络

# 每一个VGG块的参数
# (1,64) num_convs=1 out_channels=64
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(*conv_blks, nn.Flatten(),
                         nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(),
                         nn.Dropout(0.5), nn.Linear(4096, 4096), nn.ReLU(),
                         nn.Dropout(0.5), nn.Linear(4096, 10))

net = vgg(conv_arch)

#观察输出情况
X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
    X = blk(X)
    print(blk.__class__.__name__, 'output shape:\t', X.shape)

#由于VGG-11比AlexNet计算量更大，因此我们构建了一个通道数较少的网络
ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

#训练
lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

 NiN

1. NiN块使用 卷积层+1*1卷积层（对每个像素增加了非线性性）

2. NiN使用全局平均池化层来代替VGG和AlexNet中的全连接层

3. 不容易过拟合，更少的参数个数

代码

import torch
from torch import nn
from d2l import torch as d2l

#NiN块
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1),
        nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1),
        nn.ReLU())

#NiN模型
net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2), nn.Dropout(0.5),
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten())

#查看每个块输出的情况
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape:\t', X.shape)

#训练模型
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

GoogleNet

1. 在GoogLeNet中，基本的卷积块被称为Inception块（Inception block）。

2. Inception块由四条并⾏路径组成（每一条路径输出的高宽维度一致，通道数累加形成concatenation）

图一

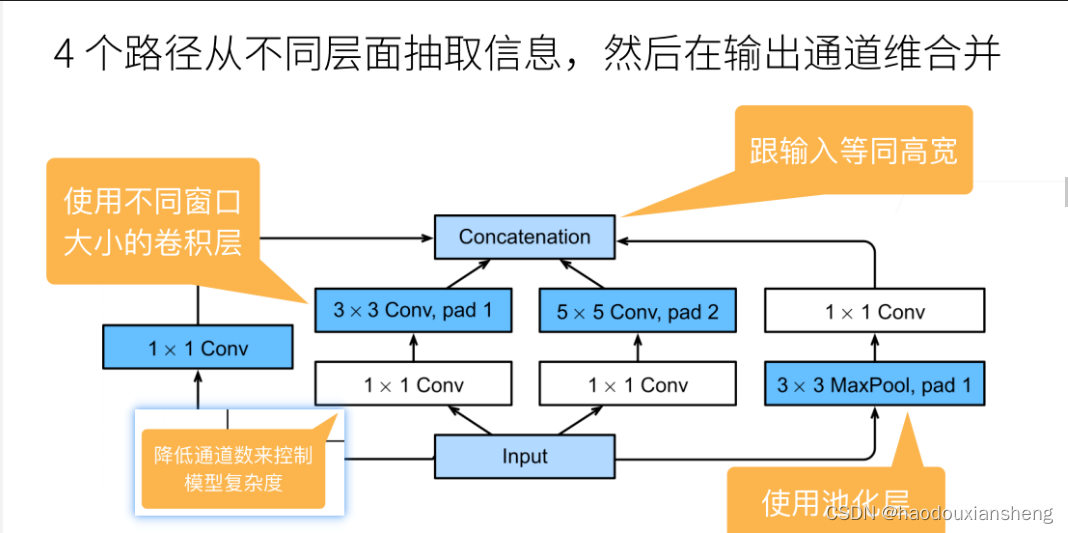
 3. GoogLeNet⼀共使⽤9个Inception块和全局平均汇聚层的堆叠来⽣成其估计值

图二

4. Inception变种

        1）Inception-BN(v2) 使用batch normalization

        2）Inception-v3 修改了Inception块

            替换5 * 5为多个3 * 3 卷积层

            替换5 * 5为1 * 7和7 * 1卷积层

            替换3 * 3为1 * 3和3 * 1卷积层

            更深

        3）Inception-V4 使用残差连接

代码

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

# Inception块 实现图一的逻辑
class Inception(nn.Module):
    #c代表输出通道数 c1，c2，c3，c4分别代表四个并行的各自的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 图一中第一条通路
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 图一中第二条通路
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1) #第二条通路的第一步
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1) #第二条通路的第二步
        # 图一中第三条通路
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 图一中第四条通路
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        # p1、p2、p3、p4代表四条不同的通路
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x)))) 
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1, p2, p3, p4), dim=1) # cat将四个并行计算的输出，按通道维度结合
    
# GoogLeNet模型 实现图二的逻辑
# b=stage 
# b1就相当于stage1
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2,
                                           padding=1))

b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1), nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

# 为了使Fashion-MNIST上的训练短小精悍，将输入的高和宽从224降到96
X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape:\t', X.shape)

#训练模型
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

批量归一化

1. 提出目的

    训练深层神经⽹络是⼗分困难的，特别是在较短的时间内使他们收敛更加棘⼿。批量规范化（batch normalization）可持续加速深层⽹络的收敛速度。

2. 批量归一化

是小批量样本的均值；+ 是小批量样本的方差（+是为了防止 为0，导致除0）； 和 是可学习参数

3. 批量归一化层

    作用时间

    （1） 全连接层和卷积层输出上，激活函数之前

    （2） 全量阶层和卷积层输入上

    作用维度

    （1）对于全连接层，作用在特征维

    （2） 对于卷积层，作用在通道维

    4. 作用

    （1） 通过选取不同的小批量数据计算均值和方差，相当于加入了噪音来控制模型的复杂度

    （2） 可以加速收敛速度，但一般不改变模型精度

代码

import torch
from torch import nn
from d2l import torch as d2l

# moving_mean 全局均值 moving_var全局方差 eps防止方差为0的加数 
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式

    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使⽤传⼊的移动平均所得的均值和⽅差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)

    else:
        assert len(X.shape) in (2, 4)

        if len(X.shape) == 2:
            # 使⽤全连接层的情况，计算特征维上的均值和⽅差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)

        else:
            # 使⽤⼆维卷积层的情况，计算通道维上（axis=1）的均值和⽅差。
            # 这⾥我们需要保持X的形状以便后⾯可以做⼴播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)

        # 训练模式下，⽤当前的均值和⽅差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        
        # 更新移动平均的均值和⽅差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var

    Y = gamma * X_hat + beta# 缩放和移位

    return Y, moving_mean.data, moving_var.data

#BatchNorm层
class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表⽰完全连接层，4表⽰卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape)) #声明为参数，需要更新
        self.beta = nn.Parameter(torch.zeros(shape))
        # ⾮模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean, self.moving_var,
            eps=1e-5, momentum=0.9)
        return Y

应用BatchNorm在LeNet 

net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4),
                    nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
                    nn.Conv2d(6, 16,
                              kernel_size=5), BatchNorm(16, num_dims=4),
                    nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
                    nn.Flatten(), nn.Linear(16 * 4 * 4, 120),
                    BatchNorm(120, num_dims=2), nn.Sigmoid(),
                    nn.Linear(120, 84), BatchNorm(84, num_dims=2),
                    nn.Sigmoid(), nn.Linear(84, 10))

# 训练
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
#看参数gamma和参数beta
net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

 ResNet

1. 随着网络加深，我们无法保证越深的神经网络就一定比浅层的神经网络更优。例如，对于⾮嵌套函数类，较复杂（由较⼤区域表⽰）的函数类不能保证更接近“真”函数（f ∗ ），而嵌套函数可以很好的解决这个问题。

2. 残差块

将第k+1块的输入（即第k块的输出）直接与第k+1块的输出结合，作为第k+1块的输出。

3.ResNet框架

类似于VGG，将VGG块替换成了ResNet块

代码

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

#ResNet块
class Residual(nn.Module):  
    def __init__(self, input_channels, num_channels, use_1x1conv=False,strides=1):
        super().__init__()
        #F_{k+1}
        self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3,padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3,padding=1)
        
        #F_k
        if use_1x1conv:
            #对输入使用1*1卷积层再和输出合并
            self.conv3 = nn.Conv2d(input_channels, num_channels,kernel_size=1, stride=strides)
        else:
            #不使用
            self.conv3 = None

        #对F_{k+1}的两个卷积层使用batchnorm   
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

        #再对合并的输出使用relu激活函数
        self.relu = nn.ReLU(inplace=True)
    
    #实现残差块的逻辑
    def forward(self, X):

        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))

        if self.conv3:
            X = self.conv3(X)
        
        #合并
        Y += X

        return F.relu(Y)

# 输入和输出形状一致
blk = Residual(3, 3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
print(Y.shape)

# 增加输出通道数的同时，减半输出的高和宽
blk = Residual(3, 6, use_1x1conv=True, strides=2)
print(blk(X).shape)

# ResNet模型

#satge1
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                                nn.BatchNorm2d(64), nn.ReLU(),
                                nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

#stage生成函数 num_residuals->stage的个数
def resnet_block(input_channels, num_channels, num_residuals,first_block=False):
    blk = []
    for i in range(num_residuals):
        #对于不是第一个使用ResNet块（b3 b4 b5)，进行高宽减半；因为b1已经将高宽减小了，所以b2没有必要再次进行减半操作
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels, use_1x1conv=True,strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk

# stage2-5使用ResNet块
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

#神经网络
net = nn.Sequential(b1, b2, b3, b4, b5, nn.AdaptiveAvgPool2d((1, 1)),nn.Flatten(), nn.Linear(512, 10))

#ResNet不同块的输出
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape:\t', X.shape)

#训练
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

DenseNet

1. DensetNet是ResNet的拓展。

2. ResNet和DenseNet的关键区别在于，DenseNet输出是连接（⽤图中的[, ]表⽰）⽽不是如ResNet的简单相加。因此，在应⽤越来越复杂的函数序列后，我们执⾏从x到其展开式的映射：

x → [x, f1(x), f2([x, f1(x)]), f3([x, f1(x), f2([x,f1(x)])]), . . .] .

3. 稠密⽹络主要由2部分构成：稠密块（dense block）和过渡层（transition layer）。前者定义如何连接输⼊和输出，⽽后者则控制通道数量，使其不会太复杂。

代码

稠密块体

import torch
from torch import nn
from d2l import torch as d2l

#定义卷积块
def conv_block(input_channels, num_channels):

    return nn.Sequential(nn.BatchNorm2d(input_channels), 
                                     nn.ReLU(),
                                     nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))

#定义稠密块：⼀个稠密块由多个卷积块组成，每个卷积块使⽤相同数量的输出通道。
#最终输出通道数=input_channels + num_convs*num_channels
class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    #在前向传播中，我们将每个卷积块的输⼊和输出在通道维上连结。
    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输⼊和输出
            X = torch.cat((X, Y), dim=1)
        return X

#调用    
blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape

过渡层：它通过1 × 1卷积层来减⼩通道数，并使⽤步幅为2的平均汇聚层减半⾼和宽，从⽽进⼀步降低模型复杂度。

def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))

blk = transition_block(23, 10)
blk(Y).shape

DenseNet模型

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

# num_channels为当前的通道数
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]

#DenseNet块
blks = []

#生成DenseNet块
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))

    # 上⼀个稠密块的输出通道数
    num_channels += num_convs * growth_rate

    # 在稠密块之间添加⼀个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2

#DenseNet模型
net = nn.Sequential(b1, *blks,
                    nn.BatchNorm2d(num_channels), nn.ReLU(),
                    nn.AdaptiveAvgPool2d((1, 1)),
                    nn.Flatten(),
                    nn.Linear(num_channels, 10))

#训练
lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())