QR分解

最新推荐文章于 2025-11-02 21:59:25 发布
原创 最新推荐文章于 2025-11-02 21:59:25 发布 · 4.1k 阅读 · 10 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文深入探讨了QR分解的三种方法：Gram-Schmidt法、修正Gram-Schmidt法及Givens旋转法。针对不同类型的矩阵，如方阵、非方阵及特定结构的矩阵，详细解析了QR分解的过程及原理，提供了丰富的数学理论与实践指导。

QR分解

对于n阶方阵A，A可逆，则存在完全QR分解，Q为n*n的正交矩阵，R为n*n的上三角矩阵。

对于非方阵的m*n(m≥n)阶矩阵A，A列满秩，存在QR分解,Q为m*n的列正交矩阵，R为n*n的上三角矩阵。

方法一：采用Gram-Schmidt法的QR分解

对于可逆矩阵A的列向量组进行Gram–Schmidt正交化，可得标准正交向量

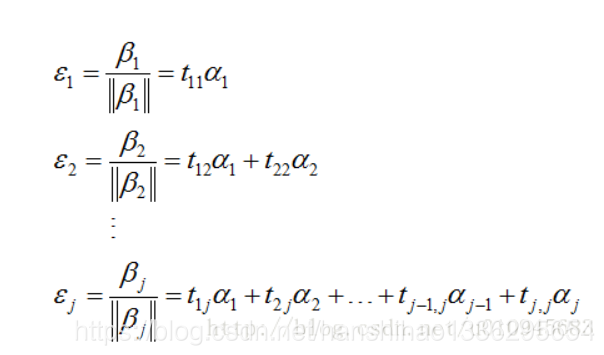
用矩阵表达即是：

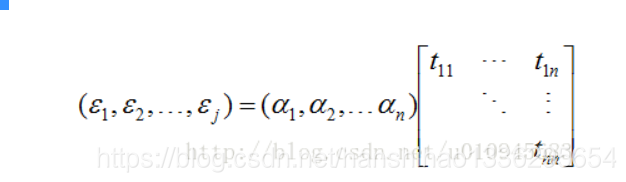
 T=(tij)，A=（），Q=()，这里注意Q是正交矩阵。若记，则A = QR，其中T的逆矩阵R仍然是上三角矩阵

方法二：采用修正Gram-Schmidt法的QR分解

        对于Gram–Schmidt正交化求正交矩阵Q提出一种改进的计算方法，改进的地方是每产生一个单位正交向量后，就用后续的向量减去它，消去其中包含这个正交向量的部分。

       将向量a_1标准正交化的结果取作 q_1，即

       \\R_{11}=||a_1||\\ \\q_1=a_1/R_{11}

       然后从a_2中减去与a_1平行的分量，然后再标准化

       \\R_{12}=q_{1}^Ha_2 \\ \\R_{22}=||a_2-q_1R_{12}|| \\ \\ q_2=(a_2-q_1R_{12})/R_{22}

        其中R_{12}表示a_2在q_1中的投影长度。a_2-q_1R_{12}表示a_2 —（a_2在q_1中的投影矢量)，R_{22}表示a_2-q_1R_{12}的大小，q_2就是a_2对应的标准正交基。

       进而，又从a_3 除去与 a_1和 a_2平行的两个分量，再进行标准正交化

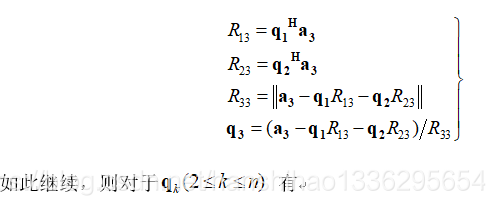
以q_1,q_2,....q_n为列向量的矩阵Q与A之间有下列关系：

A=QR

方法三：采用Givens旋转的QR分解

 Givens旋转也可以用来计算QR分解。以4*3的矩阵为例说明Givens QR分解的思想

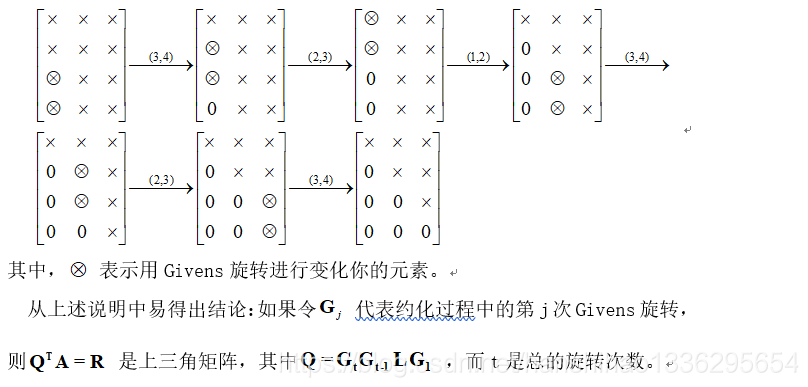
参考：https://blog.youkuaiyun.com/u010945683/article/details/45972819

 

QR分解法(QR decomposition)
cocoonyang的专栏
11-19 5900
QR decomposition divides a m by n matrix AAA into a product of an orthogonal matrix QQQ and an upper triangular matrix RRR: A=QRA=QR A = Q R Thus Ax=b=>QRx=b=>QTQRx=QTb=>Rx=QTbAx=b=&gt...
矩阵分析之QR分解
Rosun
10-24 1万+
矩阵分析之QR分解 1.定义QR分解法是目前求一般矩阵全部特征值的最有效并广泛应用的方法，一般矩阵先经过正交相似变化成为Hessenberg矩阵，然后再应用QR方法求特征值和特征向量，在分解过程中利用Gram−SchmidtGram-Schmidt正交化。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法。
线性代数 - QR分解（QR Decomposition）
最新发布
二分掌柜的
11-02 1535
flyfish
最优化方法——QR Factorization
weixin_51128278的博客
10-29 4410
最优化方法——QR Factorization前言一、QR分解二、QR分解方法1.GS QR2.修正的GS QR3.Householder三、性能比较总结 肝！ 前言 Matrix Inverse Orthogonal Matrices 前面的两篇blog主要是回顾一下线代知识，打一打基础 这三周学习的QR分解真的又双叕打开了我学习线性代数的格局，总觉得自己的数学真的是太过浅薄，总为那些优美的算法感到惊艳。于是打算整理三篇来好好地捋捋QR分解的理论和实验。（老话重提：不是为了完成DDL而作的blog）
矩阵分析——QR分解
热门推荐
GG的专栏
05-25 7万+
Gram-Schmidt正交化        在提到矩阵的QR分解前，必须要提到Gram–Schmidt方法，理论上QR分解是由Gram–Schmidt正交化推出来的。那么Gram–Schmidt正交化究竟是什么呢？        在三维空间存在直角坐标系，其中任意一点都可以由(x,y,z)坐标唯一确定，在这个坐标系中，X、Y、Z三轴都是相互正交(垂直)的。那么在n维欧式空间也应该
精选资源
QR 分解：QR 分解或因式分解（Householder Reflections Approach）-matlab开发
05-29
在线性代数中，QR 分解，也称为 QR 分解或 QU 分解是将矩阵 A 分解为正交矩阵 Q 和上三角矩阵 R 的乘积 A = QR。 QR 分解通常用于求解线性最小二乘问题，是特定特征值算法（QR 算法）的基础。 参考： 使用MATLAB:...
精选资源
QR分解_qr分解_
09-28
QR分解是一种在数值线性代数中至关重要的矩阵分解技术，它将任意的方阵或矩形矩阵转化为一个正交矩阵Q和一个上三角矩阵R的乘积形式。这一过程通常被称为QR分解或QR算法，它在许多领域，如线性最小二乘问题、特征值...
精选资源
matlab进行豪斯霍尔德变换与QR分解
11-25
在MATLAB中，豪斯霍尔德变换（Householder Transformation）和QR分解是两种非常重要的线性代数操作，它们在解决各种问题时起到关键作用，尤其是处理矩阵特征值问题。下面将详细介绍这两个概念以及如何在MATLAB中实现...
精选资源
简单 SVD：使用 QR 分解的 SVD 计算-matlab开发
05-31
QR 分解是另一种矩阵分解方法，将矩阵 A 分解为一个正交矩阵 Q 和一个上三角矩阵 R，即： \[ A = QR \] 在 MATLAB 中，可以使用 `qr` 函数对矩阵进行 QR 分解。QR 分解与 SVD 的联系在于，通过 QR 分解可以间接...
精选资源
更新瘦QR分解：当A被修改时更新A的现有QR分解，例如排名第一更新，删除或插入行或列。-matlab开发
05-31
修改 A 时更新 A 的细 QR 分解。 当 A 的维度很大（例如 5000×50）时，这些函数的运行速度比 qr 快。 等级一更新：rankoneupdate(Q, R, v, u): 当 A = A + vu' 时更新 A 的细 QR 分解。 例子： A = rand(5,3); v =...
MATLAB QR分解
11-25
矩阵论作业，让写的矩阵QR分解程序，按施密特正交化、归一化，得到酉阵Q和上三角R
矩阵QR分解的三种方法_李建东.pdf
07-19
线性代数中的基本内容，本资料总结了三种QR分解中的经典方法，具体包括：矩阵的 QR分解可利用 Schmidt正交化、矩阵的初等变换以及 Givens变换方法，这是学习QR分解的宝贵资料。若 n阶实非奇异矩阵 A可以分解为正交矩阵 Q与实非奇异上三角矩阵 R的乘积 ,即 A=QR,则称该分解式为矩阵 A的 QR分解 ;进而 A是 m×n列满秩矩阵 ,若 A=QR,其中 Q是 m×n矩阵 , Q T Q=E(称 Q为列正交矩阵), R为非奇异上三角矩阵,也称为矩阵 A的 QR分解.
qr分解
06-01
### QR分解的概念与实现方法 QR分解是一种将矩阵分解为正交矩阵和上三角矩阵乘积的形式。具体而言，任意一个实数方阵 \( A \) 可以被分解为 \( A = QR \)，其中 \( Q \) 是一个正交矩阵（满足 \( Q^TQ = I \)），\( R \) 是一个上三角矩阵[^2]。 #### QR分解的数学定义 对于一个 \( m \times n \) 的矩阵 \( A \)，QR分解的目标是找到两个矩阵 \( Q \) 和 \( R \)，使得： \[ A = QR \] - \( Q \) 是一个 \( m \times n \) 的矩阵，其列向量是标准正交的。 - \( R \) 是一个 \( n \times n \) 的上三角矩阵。 #### QR分解的实现方法 QR分解可以通过多种算法实现，常见的包括 Gram-Schmidt 正交化、Householder 变换和 Givens 旋转等方法[^2]。 1. **Gram-Schmidt 正交化** Gram-Schmidt 方法通过逐步构造正交基来实现 QR 分解。假设矩阵 \( A \) 的列向量为 \( a_1, a_2, \dots, a_n \)，则可以按照以下步骤进行： - 初始化 \( q_1 = \frac{a_1}{\|a_1\|} \)。 - 对于每个后续向量 \( a_k \)，从 \( a_k \) 中减去它在之前所有正交向量上的投影，得到新的正交向量 \( b_k \)，然后将其标准化为 \( q_k = \frac{b_k}{\|b_k\|} \)。 - 构造矩阵 \( Q \) 的列向量为 \( q_1, q_2, \dots, q_n \)，并计算 \( R \) 为 \( R = Q^T A \)。 下面是一个基于 Gram-Schmidt 正交化的 Python 实现示例： ```python import numpy as np def gram_schmidt_qr(A): m, n = A.shape Q = np.zeros((m, n)) R = np.zeros((n, n)) for j in range(n): v = A[:, j] for i in range(j): R[i, j] = np.dot(Q[:, i].T, A[:, j]) v = v - R[i, j] * Q[:, i] R[j, j] = np.linalg.norm(v) Q[:, j] = v / R[j, j] return Q, R # 示例矩阵 A = np.array([[12, 9, -4], [7, 4, 5], [6, -3, 21], [6, 15, 8]], dtype=float) Q, R = gram_schmidt_qr(A) print("Q:\n", Q) print("R:\n", R) ``` 2. **Householder 变换** Householder 方法通过构造一系列反射矩阵来实现 QR 分解。这种方法通常比 Gram-Schmidt 更数值稳定。每次反射会将矩阵的一列消去到只剩下一个非零元素，从而逐步形成上三角矩阵 \( R \)。 3. **Givens 旋转** Givens 方法通过构造一系列平面旋转矩阵来实现 QR 分解。每次旋转会将矩阵的一个元素变为零，从而逐步形成上三角矩阵 \( R \)。 #### 数值稳定性与应用 在实际应用中，QR 分解常用于求解线性方程组、最小二乘问题以及特征值计算等问题。由于 Gram-Schmidt 方法可能存在数值不稳定性，因此在需要高精度的情况下，通常推荐使用 Householder 或 Givens 方法[^1]。 --- ###
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值