线性DP

目录

0x01线性dp

线性动态规划，是较常见的一类动态规划问题，其是在线性结构上进行状态转移，这类问题不像背包问题、区间DP等有固定的模板。
特点：转移方程线性
形似 $f_i=F(j)(j\le i)$
一般会将状态设计为$f_{i,s}$,表示在区间[0/1,i]中限制条件为s的方案数/答案

[常见问题]

1) 序列问题

LIS 问题（Longest Increasing Subsequence），最长上升子序列.

显然，子序列无需连续，当前的最长上升子序列必定由前面一个最大值比当前小的最长上升子序列传递而来。
故有：$f_i=\max (f_j)+1$
一个简单优化：维护$k=\max (f_1,f_2,\cdot \cdot \cdot ,f_{i-1})$,则有 $f_i=k+1$

LCS 问题（Longest Common Subsequence），求序列的最长公共子序列。

显然，LCS的状态与A,B序列都要有相关性，设计为$f_{i,j}$，即A取前i，B取前j位时LCS长度。
转移来源也很明显：$f_{i-1,j-1},f_{i,j-1},f_{i-1,j}$
显然有 $f_{i,j}=max(max(f_{i-1,j-1},f_{i,j-1},f_{i-1,j})(不增加长度),f_{i-1,j-1}+1(增加长度且仅当A_i=B_j))$

LCIS 问题（Longest Common Increasing Subsequence），求序列的最长公共上升子序列。

$LIS+LCS=LICS$
在LCS基础上加上升判断

2) 字符串编辑距离

字符串编辑距离，即 Levenshtein 距离，是俄国科学家 Vladimir Levenshtein 提出的概念，是指从一个字符串修改到另一个字符串时，编辑单个字符所需的最少次数，编辑单个字符允许的操作有：替换、插入、删除。

我们分类讨论：
替换：将a[i]替换为b[i],当a[i] = b[i]时不增加次数，否则增加一步。
插入、删除 ： 必定增加一步

接着是状态设计，设$f_{i,j}$为原串前i位变为新串前j位的最小次数。
1.插入：插入会让原串的长度+1，所以是从$f_{i,j-1}$转移而来。
2.删除：删除会让原串的长度-1,让多余/错误的i位消失，所以是从$f_{i-1,j}$转移而来。
3.替换：替换会让原串的i位变成新串j位，所以是从$f_{i-1,j-1}$转移而来。
参考下图：

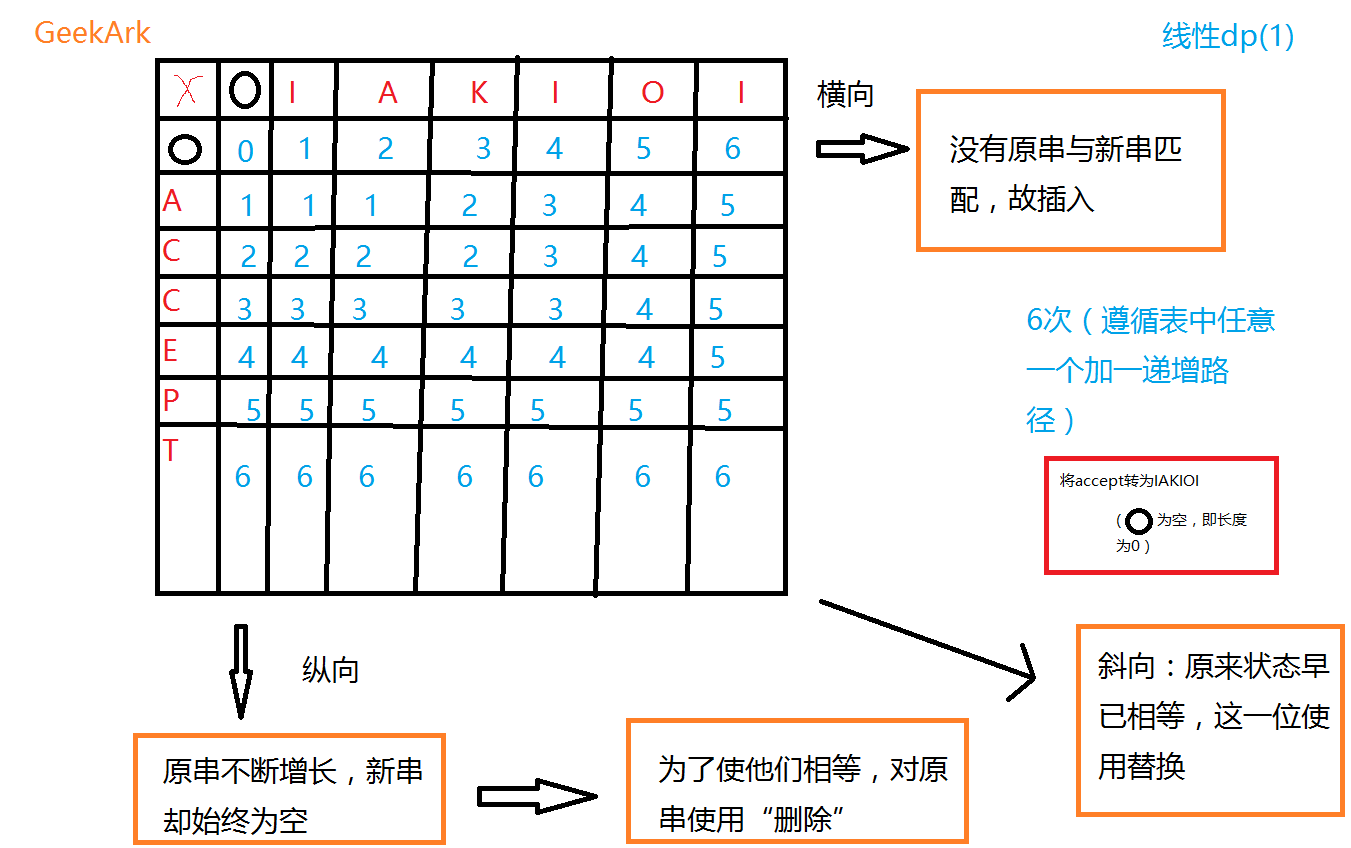
故推出转移方程：$f_{i,j}=min(min(f_{i-1,j}+1,f_{i,j-1}+1),f_{i-1,j-1}+(a_i==b_j?0:1))$
3) 最大和问题

[最大子序列和] 对于给定序列 a1,a2,a3……an 寻找它的连续的最大和子数组

由于他是连续的最大和子数组，所以$f_i$便只能从$f_{i-1}$传递而来。
对于每个位置$i$来说，他可以选择作为上一个连续子序列的成员，也可以另起一个新的连续子序列。
所以，$f_i=max(f_{i-1}+a_i,a_i)$

[最大子矩阵和] 给定一个 n 行 m 列的整数矩阵 A，现在要求 A 的一个子矩阵，使其各元素之和为最大

我们从极端情况开始思考：

• 答案矩阵大小为1*$k$
  本题将退化为最大子序列和。
• 答案矩阵大小为2*$k$：
  因为矩阵必须竖着一起取，所以我们可以将竖列都加在一起：
  如矩阵：
  $[0,-1,-5,3$
  $9,0,-8,5]$
  转换为
  $[9,-1,-13,8]$
  (退化为最大子序列和)
  答案为：
  9
  ($[0$
  $9]$)
• $3\ast k,4\ast k,\cdot \cdot \cdot$
  与2*$k$类似

[数字三角形] 给出一个数字三角形，现在要从左上角走到第 i 行，每一步只能走到相邻的结点，求经过的结点的最大数字和。如：
1
2 3
4 5 6

反着来想，从第$i$行走到第1行，效果不变，输出时只需输出$f_{1,1}$即可。
状态转移方程也很裸，$f_{i,j}=max(f_{i+1,j},f_{i+1,j+1})+a_{n,j}$
给$f_{n,j}$初始化为$a_{n,j}$

extend 1 2023/1/11
根据题目设计优良的状态与状态转移方式
例题：P4310 绝世好题
显然，这道题设计状态为$f_i$ , $i$表示当前已考虑区间[1,$i$]，$f_i$表示此时满足要求的最长子序列长度。
但如果按常规方法${\sum }_{i=1}^n{\sum }_{j=1}^{i-1}{f}_i=max(f_i,f_j+((a_i\&a_j)!=0?1:0))$,时间复杂度为$\Theta (n^2)$
如何优化时间？
显然，循环$i$是无法优化的，我们只好从$j$下手。
先理解循环$j$的意义：题目中的转移限制条件$(b_i\&b_{i-1})!=0$，即序列中两个数的二进制运算。
我们刚刚的做法是从暴力寻找适合的$j$，可以试试看从转移限制条件入手。
由于使用了$\&$这个按位二进制运算，，且$a_i\le 10^9$,换算成二进制就是30位。也就是说，在$i$时能增加的子序列只有30种情况（判断a[i]为1的位），比N种好多了
于是我们可以更改一下状态的定义：
$f_i$：到目前为止最后一项第i位为1的最大子序列长度.

#include <bits/stdc++.h>
using namespace std;
int n,b,ans=0;
int f[32];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>b;
		int k=0;
		for(int j=0;j<=30;j++)
		if((1<<j)&b) k=max(f[j]+1,k);//上一轮j+1位为1的可以+1
		for(int j=0;j<=30;j++)
		if((1<<j)&b) f[j]=max(f[j],k);//加上本数后，最值为k，与本数某一位相同的因为本数的关系也必须更新
		ans=max(ans,k);
	}
	printf("%d\n",ans);
	return 0;
}