DFS 专题1 迷宫可行路径数

原创已于 2023-07-30 22:48:34 修改 · 179 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法

于 2023-07-30 22:47:34 首次发布

算法笔记专栏收录该内容

95 篇文章

订阅专栏

该代码示例展示了如何用深度优先搜索(DFS)解决迷宫路径问题。程序通过递归遍历所有可能的路径，计算从起点到终点的可行路径数量。在过程中，使用vis[][]数组记录已访问的坐标，防止重复探索，并通过dx[]和dy[]数组进行坐标移动。

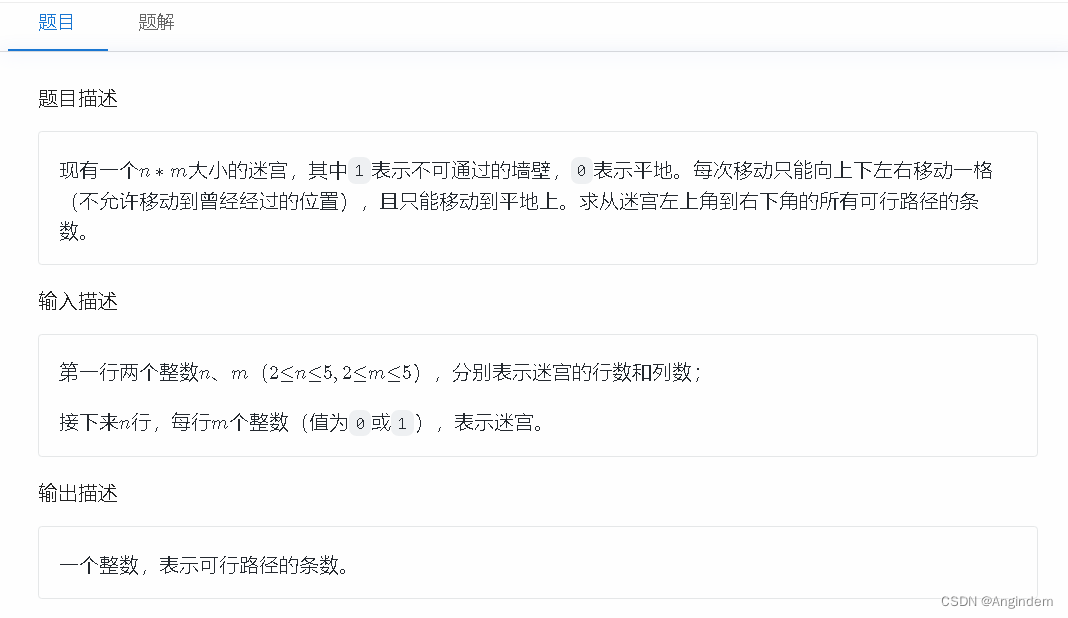
题目：

样例1

输入
3 3 0 0 0 0 1 0 0 0 0

输出
2

思路：

利用递归的思想，每一步到哪到哪，代码详解如下：

#include <iostream>
using namespace std;
const int N = 500;

// 这里是控制坐标移动操作，
// 错位即可一步一步的移动
int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};

int n, m;	// 迷宫大小变量

int ans;	// 答案，可行路径的条数

int g[N][N];	// 迷宫二维数组

bool vis[N][N];		// 这里是标记所走过的坐标

// 这里是 DFS 递归条件，也就是往前走的条件
bool isRun(int bx, int by)
{
	return (bx >= 0 && bx < n && by >= 0 && by < m && !g[bx][by] && !vis[bx][by]);
}


void DFS(int x, int y)
{
	// 递归边界，如果到达了目的地，统计路径
	if (x == n - 1 && y == m - 1)
	{
		ans++;
		return ;
	}

	// 关键是这里：
	// 这里表示的是标记当前坐标所走的坐标
	vis[x][y] = true;


	// 这里开始移动坐标
	for (int i = 0; i < 4; ++i)
	{
		// 这里是尝试往前走
		int bx = x + dx[i];
		int by = y + dy[i];

		if (isRun(bx, by))
		{
			// 如果可以行走，则开始标记
			vis[bx][by] = true;

			DFS(bx, by);		// 递归，往前走

			// 往前走完后，后退，
			// 恢复原来状态
			vis[bx][by] = false;
		}
	}
	return ;
}


int main()
{
	cin >> n >> m;
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < m; ++j)
		{
			cin >> g[i][j];
		}
	}

	DFS(0, 0);		// 从左上角坐标开始

	cout << ans << endl;

	return 0;
}

最后提交：