斐波那契数列的定义如下:
F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2) (n >= 2)
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)
给出n,求F(n),由于结果很大,输出F(n) % 1000000009的结果即可。
Input
输入1个数n(1 <= n <= 10^18)。
Output
输出F(n) % 1000000009的结果。
Input示例
11
Output示例
89
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。
作者:王希
链接:http://www.zhihu.com/question/23582123/answer/40464211
来源:知乎
矩阵递推关系
学过代数的人可以看出,下面这个式子是成立的:
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/202c202d7ff7b6e11c1b3436fd789ad5.png" data-rawwidth="284" data-rawheight="69" class="content_image" width="284"&gt;不停地利用这个式子迭代右边的列向量,会得到下面的式子: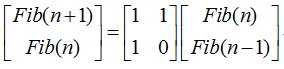 不停地利用这个式子迭代右边的列向量,会得到下面的式子:
不停地利用这个式子迭代右边的列向量,会得到下面的式子:
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/4f08da760eb450bde73ad90c04d98f30.png" data-rawwidth="270" data-rawheight="70" class="content_image" width="270"&gt;这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。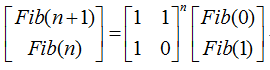 这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。
快速幂_百度百科是利用结合律快速计算幂次的方法。比如我要计算
这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。
快速幂_百度百科是利用结合律快速计算幂次的方法。比如我要计算
![2^{20}]() ,我们知道
,我们知道
![2^{20} = 2^{16} * 2^{4}]() ,而
,而
![2^{2}]() 可以通过
可以通过
![2^{1} \times 2^{1}]() 来计算,
来计算,
![2^{4}]() 而可以通过
而可以通过
![2^{2}\times 2^{2}]() 计算,以此类推。通过这种方法,可以在O(lbn)的时间里计算出一个数的n次幂。快速幂的代码如下:
计算,以此类推。通过这种方法,可以在O(lbn)的时间里计算出一个数的n次幂。快速幂的代码如下:
学过代数的人可以看出,下面这个式子是成立的:
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/202c202d7ff7b6e11c1b3436fd789ad5.png" data-rawwidth="284" data-rawheight="69" class="content_image" width="284"&gt;不停地利用这个式子迭代右边的列向量,会得到下面的式子:
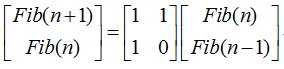 不停地利用这个式子迭代右边的列向量,会得到下面的式子:
不停地利用这个式子迭代右边的列向量,会得到下面的式子:
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/4f08da760eb450bde73ad90c04d98f30.png" data-rawwidth="270" data-rawheight="70" class="content_image" width="270"&gt;这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。
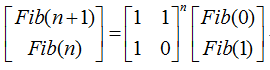 这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。
快速幂_百度百科是利用结合律快速计算幂次的方法。比如我要计算
这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。
快速幂_百度百科是利用结合律快速计算幂次的方法。比如我要计算
#include <iostream>
#include <algorithm>
#include <cmath>
#define MOD 1000000009
#define N 2
using namespace std;
struct Matrix
{
long long v[N][N];
};
Matrix matrix_mul(Matrix A, Matrix B, long long m)
{
Matrix ans;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
ans.v[i][j] = 0;
for (int k = 0; k < N; k ++)
{
ans.v[i][j] += (A.v[i][k] * B.v[k][j]) % m;
}
ans.v[i][j] %= m;
}
}
return ans;
}
Matrix matrix_pow(Matrix C, long long n, long long m)
{
Matrix ans = {1, 0, 0, 1};
while (n)
{
if (n & 1)
ans = matrix_mul(ans, C, m);
C = matrix_mul(C, C, m);
n >>= 1;
}
return ans;
}
int main()
{
long long n;
Matrix temp1 = {1, 1, 1, 0}, temp2 = {1, 0, 1, 0}; // temp2{f[2],0,f[1],0}!!!!!
while (cin >> n)
{
if (n < 2)
{
cout << 1 << endl;
continue;
}
Matrix res = matrix_pow(temp1, n - 2, MOD);
res = matrix_mul(res, temp2, MOD);
cout << res.v[0][0] << endl;
}
return 0;
}









 本文介绍了一种使用矩阵快速幂算法高效计算斐波那契数列第n项的方法,该方法适用于大整数计算场景,避免了传统递归方式的效率瓶颈。
本文介绍了一种使用矩阵快速幂算法高效计算斐波那契数列第n项的方法,该方法适用于大整数计算场景,避免了传统递归方式的效率瓶颈。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








