本博文为本人学习P3P算法的学习笔记~
先给出论文的链接(https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1217599)
《Complete solution classification for the perspective-three-point problem》
理论
相机位姿估计就是通过几个已知坐标的特征点,以及他们在相机照片中的成像,求解出相机位于坐标系内的坐标与旋转角度。
P3P
PnP(Perspective-n-Point)是求解3D到2D点对运动的方法。它描述了当知道N个3D空间点及其投影位置时,如何估计相机的位姿。即给出n个3D空间点时,如何求解相机的位姿。
P3P需要利用戈丁的3个点的几何关系。输入数据为3对3D-2D匹配点。记3D点为A、B、C,2D点为a,b,c,其中,小写字母代表点的为对应大写字母代表的带你在相机成像平面上的投影。此外,P3P还需要使用一对验证点,从可能的解中选出正确的那一个(验证点记为D-d),相机的光心为O。请注意,我们知道的是ABC三个点在世界坐标系中的坐标,而不是在相机坐标系中的坐标。
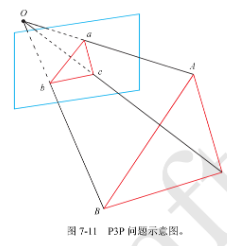
由图可得,显然有如下相似三角形的关系
![]()
采用余弦定理,有
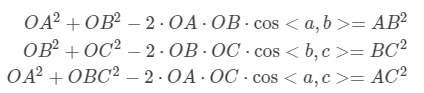
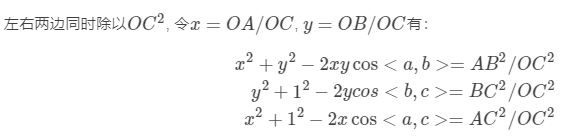
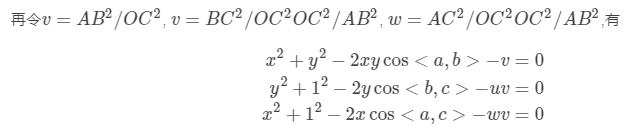
将1代入2、3有
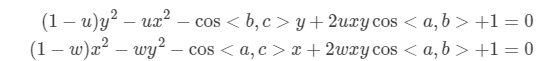
2D点的图像坐标已知,3个余弦角已知。3D点的坐标已知,只有xy未知。可以采用吴消元法来解上述方程。该方法最多可以获得4个解,但可以通过第四个点,来获得最可能的解。进一步地,EPnP(需要4对不共面的点)、UPnP等则是利用更多的信息来迭代,对相机的位姿进行优化,以尽可能消除噪声的影响。
进一步地,对于估计获得的位姿,构建最小二乘优化问题对估计值进行调整(Bundle Adjustmen)
Bundle Adjustmen(光速法平差。最小化重投影误差)
把PnP问题构建成一个定义于李代数上的非线性最小二乘问题。BA算法优化的是sum of reprojection error,这是一个(geometric distance) 几何距离可以转换成一个least squares problem, 如果nosie是gaussian的话,那就是一个最大似然估计(maximum likelihood estimator),是这种情况下所能得到的最优解了。 这个reprojection error的公式是非线性的,所以这个least squares problem得用迭代法来求解:般都是用Gauss-Newton 法或者LM算法迭代求解。bundle adjustmen由于是特定的形式,所以可以化成sparse matrix 的形式,这样计算量大大减小了。
基于视觉的SLAM算法里面使用了图优化替代了原来的滤波器,这里所谓的图优化其实也是指BA算法。BA本质是一个优化模型,其目的就是最小化重投影误差。如下图所示
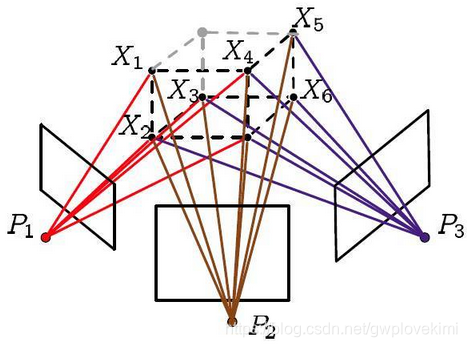
光束则是指图中的三维空间的投影点到像平面上的光束。(光束法正是强调优化模型如何建立的)。而所谓的第一次投影就是指相机在拍照的时候三维空间点投影到图像上。然后利用这些图像对一些特征点进行三角定位(利用几何信息构建三角形来确定三维空间点的位置)。最后利用计算得到的三维点的坐标(注意不是真实的)和计算得到的相机矩阵(当然也不是真实的)进行第二次投影,也就是重投影。而重投影的误差是指真实三维空间点在图像平面上的投影(也就是图像上的像素点)和重投影(其实是用我们的计算值得到的虚拟的像素点)的差值。通过将这些差值的和最小化获取最优的相机参数及三维空间点的坐标。
优化的过程,即图优化。如下图所示。![]()
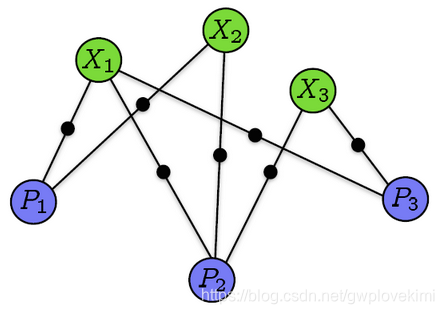
接下来可以通过这个图来构建优化模型了。

BA现在基本都是利用LM(Levenberg-Marquardt)算法并在此基础上利用BA模型的稀疏性质来进行计算的,LM算法是最速下降法(梯度下降法)和Gauss-Newton的结合体。优化函数如下图所示
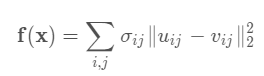
最速下降法(沿梯度的负方向去迭代寻找使函数最小的变量值)
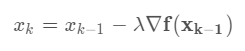
最速下降法保证了每次迭代函数都是下降的,在初始点离最优点很远的时候刚开始下降的速度非常快,但是最速下降法的迭代方向是折线形的导致了收敛非常非常的慢。
Newton方法
首先将函数利用泰勒展开到二次项
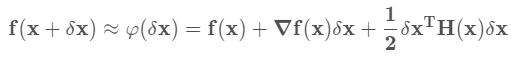
H为Hessian矩阵,是二次偏导矩阵。
![]()
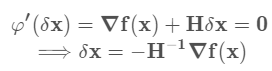
Newton型方法收敛的时候特别快,尤其是对于二次函数而言一步就可以得到结果。但是该方法有个最大的缺点就是Hessian矩阵计算实在是太复杂了,并且Newton型方法的迭代并不像最速下降法一样保证每次迭代都是下降的。
Gauss-Newton方法

LM方法

LM算法就由此保证了每次迭代都是下降的,并且可以快速收敛。






再通过3D-3D的点对,来计算相机的位姿。
补充说明重投影误差
重投影误差:是像素坐标(观测到的投影位置)与3D点按照当前估计的位姿进行投影得到的位置相比较得到的误差。(用估算出来的旋转矩阵与平移矩阵,再次进行投影,看与检测的误差,为重投影误差,但误差最小时,为当前最好的变换矩阵)
如下图所示,我们通过特征匹配知道,观测值![]() 和
和  是同一个空间点
是同一个空间点 的投影,
的投影, 的投影
的投影 与观测值
与观测值 之间有一定的距离,也就是重投影误差。于是我们调整相机的位姿,使这个距离变小,由于这个调整需要考虑很多个点,所以最后每个点的误差通常不会精确到0
之间有一定的距离,也就是重投影误差。于是我们调整相机的位姿,使这个距离变小,由于这个调整需要考虑很多个点,所以最后每个点的误差通常不会精确到0
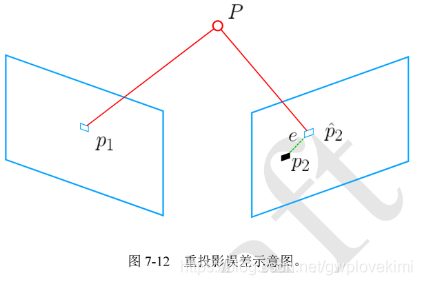
重投影误差是指投影的点(理论值)与图像上的测量点的误差。例如在标定的时候我们经常用到重投影误差作为最终标定效果的评价标准,我们认为标定板上的物理点是理论值,它经过投影变换后会得到理论的像素点a,而测量的点经过畸变矫正后的像素点为a′a′,它们的欧氏距离||a−a′||2||a−a′||2即表示重投影误差。
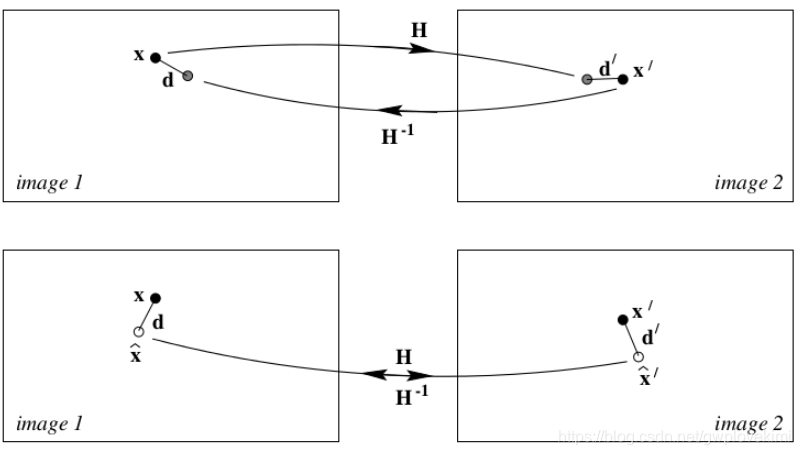
对称转移误差
左右图像上某一对测量的得到的匹配点,各自经过单应变换得到各自的理论匹配点,对称转移误差是指这一对测量得到的匹配点与另一张图像变换过来的理论匹配点的欧式距离,如下图所示
ICP(Iterative Closest Point,迭代最近点来求解)
位姿估计是计算机视觉领域一个基本问题。若已获得合作标志在摄像机坐标系下的坐标值,一般情况可采用奇异值分解或最小二乘的方法求解位姿信息中的旋转矩阵与平移矩阵,满足

其中下标c表示Camera,w表示World。


如上图所示,当合作标志特征点个数为3时,且3点不共线时,记


ICP统指匹配好的两组点间运动估计问题。
ICP算法是对于X中的每一个点用当前的R和 t在Y中找最近的点(比如用欧式距离),然后这两个点就成了一对了,每个点都有了对应的映射点,用每一对的坐标列一个方程,就得到一系列的方程。
重复迭代运行上述过程,直到均方差误差小于某个阀值。
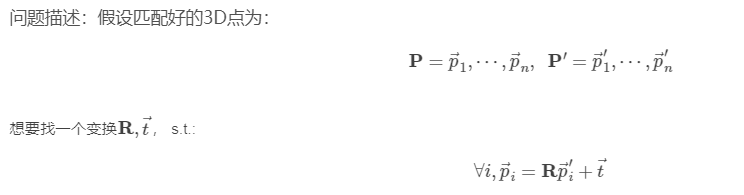
ICP的求解主要有线性代数的求解(SVD)和非线性优化的求解(BA).(具体可参考https://blog.youkuaiyun.com/luohuiwu/article/details/80748213)
实验测试
对于PnP问题可以直接调用Opencv中的库函数solvePnP
参考材料
https://www.cnblogs.com/singlex/p/pose_estimation_0.html
https://blog.youkuaiyun.com/luohuiwu/article/details/80722542
《视觉SLAM十四讲》
https://github.com/vshawn/Shawn_pose_estimation_by_opencv
https://www.cnblogs.com/Jessica-jie/p/7739775.html
https://blog.youkuaiyun.com/OptSolution/article/details/64442962(BA算法的介绍,写得很好)
https://blog.youkuaiyun.com/sinat_17496535/article/details/51673285(关于重投影误差与对称转移误差)










 本文是学习P3P算法的笔记。介绍了相机位姿估计,P3P利用3对3D - 2D匹配点求解相机位姿,还可通过验证点选解。阐述了Bundle Adjustmen最小化重投影误差,以及对称转移误差、ICP算法。最后提到PnP问题可调用Opencv库函数求解。
本文是学习P3P算法的笔记。介绍了相机位姿估计,P3P利用3对3D - 2D匹配点求解相机位姿,还可通过验证点选解。阐述了Bundle Adjustmen最小化重投影误差,以及对称转移误差、ICP算法。最后提到PnP问题可调用Opencv库函数求解。
















 1834
1834

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








