本篇博客参考了2018年IJCAI会议上的城市计算方向的一篇paper《GeoMAN: Multi-level Attention Networks for Geo-sensory Time Series Prediction》,作者是原微软亚洲研究院研究员、现京东金融集团副总裁、首席数据科学家郑宇。其实城市计算这个概念我之前也只是听说过,即利用大数据和人工智能技术来解决城市里的各种交通、规划、环境、能源、商业和公共安全等问题。本文以水质量预测和空气质量预测为背景,通过神经网络的建模方法来预测未来一段时间内的水质量和空气质量。
首先需要解决问题的场景描述如下图所示:
上图是北京市地区的空气检测站的分布图,每一个检测站被称之为一个sensor,每一个sensor在一天之内都会间隔固定的时间(一般是5min)采集空气数据,其中包括:温度,湿度,PM2.5(这一项是我们最在意的,也是本文需要预测的指标),NO,NO2,以及各个方向的风力大小等19个维度的属性特征。这种场景的数据特点就是,每一个sensor地理位置是不会变化的,它们之间的相对位置也是不变的,但是由于是每隔一段时间就会采集一次数据,因此每一个sensor都会产生一系列的时序数据。假设我们sensor的数量是NgNg个,每一个sensor采集的属性特征数为NlNl。那么我们的任务就是,给一个时间间隔TT范围内的所有sensor数据,来预测某一个在接下来的T+τT+τ时间段内的某一维属性特征序列值。从问题描述我们可以知道,对于其中的一个sensor XX,它在一段时间内产生的数据可以用矩阵来表示,这个矩阵的维度是Nl∗TNl∗T。
从问题分类上看,这是一个时间序列的回归问题,损失函数也就是简单的均方损失函数。由于是序列生成序列,故本文采用的是经典的seq2seq架构(在NLP中常用于机器翻译和摘要生成等任务),因此一定会使用encoder-decoder架构,同时由于该任务的特殊性,本文在decoder生成阶段又巧妙的引入了其他的外部信息(比方说sensor对应的poi信息,天气信息以及sensor ID信息),显著地提升了模型的性能。整个模型如下所示:
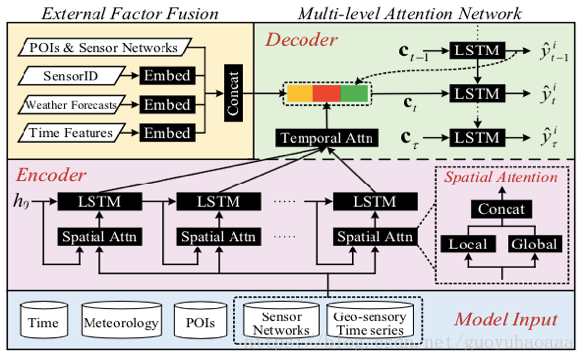
可以看出在encoder和decoder该模型都使用了LSTM,在LSTM的输入部分可以看到一个被称之为“Spatial Attn”的结构,从右边放大的框图可以看出这个结构由“Local”和“Global”拼接而成即[xlocalt;xglobalt][xtlocal;xtglobal],这个“Local”指的是当前被预测的sensorisensori的信息编码,“Global”指的则是其他sensor的信息编码,这两个编码过程中都是用了Attention机制。下面就来详细讲解:
Local Spatial Attention
ekt=VTltanh(Wl[ht−1;St−1]+Ulxi,k+bl)etk=VlTtanh(Wl[ht−1;St−1]+Ulxi,k+bl) (1)
αkt=exp(ekt)∑Nlj=1exp(ejt)αtk=exp(etk)∑j=1Nlexp(etj) (2)
其中vl,bl∈RT,Wl∈RT∗2m,Ul∈RT∗Tvl,bl∈RT,Wl∈RT∗2m,Ul∈RT∗T是模型需要训练的参数。
xi,kxi,k指的是第i个sensor的第k维特征在T时间段内的收集的特征向量,由于是local 信息的编码,因此对sensorisensori中所有的特征都进行同样的操作,得到t时刻的权重αα向量(时间信息在1式中的[ht−1;st−1][ht−1;st−1]就体现出来了)。那么xlocalt=(α1txi,1t,α2txi,2t....αNltxi,Nlt)xtlocal=(αt1xti,1,αt2xti,2....αtNlxti,Nl),其中xi,1txti,1代表了sensorisensori在第t时刻的第1维属性的取值。这个local信息编码告诉我们,在同一个sensor内部的所有采集的属性特征信息之间是由关系的。
Global Spatial Attention
既然是使用attention技巧对Global信息进行编码,那么肯定要计算目标sensorisensori和其他的sensorlsensorl的相关度(特别是在需要预测的特征维度y上的):
glt=vTgtanh(Wg[ht−1;st−1]+Ugyl+W#gXlug+bg])gtl=vgTtanh(Wg[ht−1;st−1]+Ugyl+Wg#Xlug+bg])
其中vg,ug,bg∈RT,Wg∈RT∗2m,Ug∈RT∗T,W#g∈RT∗Nlvg,ug,bg∈RT,Wg∈RT∗2m,Ug∈RT∗T,Wg#∈RT∗Nl。需要注意的是,ylyl是其他sensor在T时间点内的目标维度上的取值序列,需要注意的是这里attention的权值计算方法:
βlt=exp((1−λ)glt+λPi,l)∑Ngj=1exp((1−λ)glt+λPi,j)βtl=exp((1−λ)gtl+λPi,l)∑j=1Ngexp((1−λ)gtl+λPi,j)
其中λλ是一个调节参数,Pi,lPi,l作为先验概率句子用来衡量sensorisensori和sensorjsensorj在空间地理位置上的相似性(如地理距离的倒数)。
那么最终 xglobalt=(β1ty1t,β2ty2t....βNgtyNgt)xtglobal=(βt1yt1,βt2yt2....βtNgytNg),即其他sensor的待预测维度信息加权编码。论文中提到,如果在实际场景中NgNg的数量太大的话,可以根据Pi,jPi,j距离相似矩阵挑选出和目标sensorisensori距离相似的前k个sensor作为简化。(从常识上来讲。距离越近的sensor之间的相关性程度越高)
Temporal Attention
由于encoder-decoder架构的性能会随着encoder序列的长度大幅度下降,因此在decoder的过程中一般会使用attention来encoder序列中选择每一时刻应该强调的序列内容,那么decoder过程中的t时刻的attention权重计算如下:
uot=vTdtanh(W#d[dt−1;s#t−1]+Wdho+bd)uto=vdTtanh(Wd#[dt−1;st−1#]+Wdho+bd)
λot=exp(uot)∑Tj=1exp(ujt)λto=exp(uto)∑j=1Texp(utj)
ct=∑To=1λothoct=∑o=1Tλtoho
其中Wd∈Rm∗m,W#d∈Rm∗2n,vd,bd∈RmWd∈Rm∗m,Wd#∈Rm∗2n,vd,bd∈Rm是模型训练的参数。
Encoder-Decoder Architecture
那么在encoder阶段,使用fefe代表LSTM的处理单元,那么LSTM每一时刻t的输入xt=[xlocalt;xglobalt]xt=[xtlocal;xtglobal],那么整个过程就有ht=fe(ht−1,xt)ht=fe(ht−1,xt)
在decoder阶段,会使用另一个LSTM进行建模,其迭代公式如下:
dt=fd(dt−1,[yit−1;ct;ext])dt=fd(dt−1,[yt−1i;ct;ext]) (3)
其中yit−1yt−1i就是sensorisensori在t-1时刻的输出值,即对t-1时刻的预测值,其计算公式如下:
yit=vTy(Wm[ct;dt]+bm)+byyti=vyT(Wm[ct;dt]+bm)+by
其中Wm∈Rn∗(n+m),bm∈Rn,vy∈Rn,by∈RWm∈Rn∗(n+m),bm∈Rn,vy∈Rn,by∈R是模型的训练参数。
同时在(3)式中,有一个前面没有提及的变量extext,这个变量编码的是“external factor”信息,即使用embedding策略对sensor 网络的poi信息,时间信息,天气信息(如果对未来的天气信息没法获取,可以借助天气预报信息)进行特征映射。
最后的损失函数就是经典的均方损失,||yi−ytruei||22||yi−yitrue||22,训练的方法采用Adam。





 介绍GeoMAN模型,一种多级注意力网络,用于地理传感时间序列预测,如空气质量预测。该模型结合局部与全局注意力机制,有效捕捉传感器间时空依赖关系。
介绍GeoMAN模型,一种多级注意力网络,用于地理传感时间序列预测,如空气质量预测。该模型结合局部与全局注意力机制,有效捕捉传感器间时空依赖关系。
















 1177
1177

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








