批量归一化(Batch Normalization)是提高神经网络性能的重要技术，它可以提高模型的泛化能力和收敛速度。BN通过对每一层的输入进行归一化处理，解决了梯度消失和梯度爆炸问题，同时能作为正则化手段减少其他正则项。在前向传播中，BN计算数据均值和方差进行归一化，通过可学习参数调整保持特征分布。反向传播时，通过链式法则更新γ和β以及权重。此外，BN还能替代局部响应归一化层，并允许使用更大的学习率，加速训练过程。
一、为什么需要归一化
1、提高泛化能力
若测试集与训练集分布不同，则会使网络的泛化能力降低。
2、提高收敛速度
若每个batch的数据分布不尽相同，那么每次迭代都需要去适应不同的分布情况；且网络前几层的变化会累积到后面的网络层（我们将这种训练过程中网络中间层数据分布的改变称之为：“Internal Covariate Shift”。），从而使训练收敛速度降低。
3、待补充
二、Batch Normalization原理
与再输入层对输入数据进行归一化处理相似，于每一层的输入之前加入BN层进行每一层的数据分布归一化。
1、借鉴思想
对输入数据的预处理通常采用白化操作，经白化处理后的数据集满足如下两个条件：
（1）特征相关性降低；
（2）数据均值、标准差归一化。
然而简单的白化处理有可能破坏上一层所学习到的特征分布，故BN层在对x近似白化处理之后引入可学习参数γ和β来还原特征分布。
2、前向传播
（1）计算数据均值；
（2）计算数据方差；
（3）对输入数据近似白化处理（归一化）；
（4）通过放缩和迁移提高数据对非线性区域的表达能力并还原上一层学习到的特征分布。
3、反向传播
通过链式求导方式求出γ与β以及相关权值。
三、Batch Normalization优势
1、解决梯度消失和梯度爆炸问题
（1）梯度消失
以sigmoid激活函数为例，
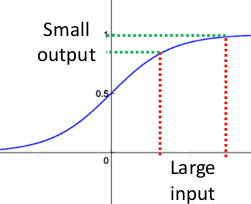
当某层的z分布在逻辑函数两边的接近水平的地方即梯度接近0的位置,那么网络反向传播至这层后梯度消失从而导致参数不再更新，且根据链式求导原则，后面的网络层求导次数较少则梯度相对浅层大，从而导致浅层基本不学习、深层一直在学习的情况出现。
（2）梯度爆炸
根据链式求导原则，若某些层的权值过大，那么在反向传播时梯度大小则会指数增加，从而造成梯度爆炸。
BN使得输入的数据分布均匀相似，消除了极端情况，从而避免了梯度消失和梯度爆炸。
2、加快训练速度
BN能减少每层的梯度变化幅度,使梯度稳定在理想的变化范围内，使得我们可以使用较大的学习率也不会导致梯度消失，从而加快训练速度。
3、提高网络泛化能力
BN本身具有一定的正则化能力，故我们可以适当减少drop out、L2正则项。
4、替换局部响应归一化层
局部响应归一化层（LRN层）借鉴侧抑制的概念，在局部神经元的活动中引入竞争机制，使相应相对较大的值更大。而BN层本身就带有归一化的能力，可替换LRN层。
5、将数据彻底打乱
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
