SVM通过最大化间隔选择最优分类超平面，避免了感知机中分类超平面的不唯一性。函数间隔和几何间隔被引入，其中几何间隔对比例变化不变，成为分类依据。通过凸二次规划问题确定最优解，支持向量决定了超平面。进一步，原始问题转换为对偶问题简化求解，最终得到最优参数w和b的表达式，支持向量在此过程中起到关键作用。
1. 原始问题
与感知机相似，SVM通过分类超平面划分数据集，分类超平面形式为：
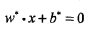
但感知机中分类超平面是不唯一的，SVM以间隔最大为依据可以唯一确定最优分类超平面，其中函数间隔定义为：
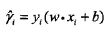
然而当参数w和b成比例变化时，虽然分类超平面没有变化，但函数间隔却变化了，故又提出了几何间隔：
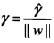
即使w和b成比例变化，几何间隔也不会改变，故不会出现多个间隔对应同一分类超平面的情况，可用作分类依据。
求解最大间隔分类超平面过程如下：
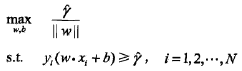
在同一个分类超平面上，w和b的同比例变化并不会影响不等式约束，故可固定函数间隔为1，则上述过程可等价为如下凸二次规划问题：
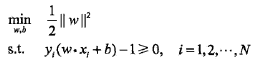
从而求得最优解w和b得到最优超平面，其中支持向量为满足下式的实例点：
最低0.47元/天 解锁文章
扫一扫
1644
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
