
华为OD机试 双机位C卷题库疯狂收录中,刷题点这里
专栏导读
本专栏收录于《华为OD机试(JAVA)真题》。
刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天优快云在线答疑。
一、题目描述
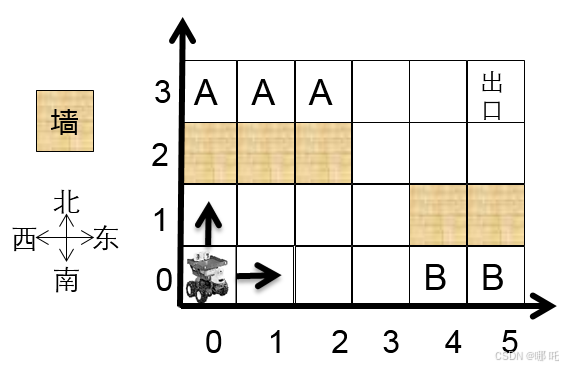
房间由XY的方格组成,例如下图为6*4的大小。每一个方格以坐标(x, y)描述。
机器人固定从方格(0, 0)出发,只能向东或者向北前进。出口固定为房间的最东北角,如下图的方格(5, 3)。用例保证机器人可以从入口走到出口。
房间有些方格是墙壁,如(4, 1),机器人不能经过那儿。
有些地方是一旦到达就无法走到出口的,如标记为B的方格,称之为陷阱方格。
有些地方是机器人无法到达的,如标记为A的方格,称之为不可达方格,不可达方格不包括墙壁所在的位置。
如下示例图中,陷阱方格有2个,不可达方格有3个。
请为该机器人实现路径规划功能:给定房间大小、墙壁位置,请计算出陷阱方格与不可达方格分别有多少个。
二、输入描述
第一行为房间的X和Y(0 < X,Y <= 1000)
• 第二行为房间中墙壁的个数N(0 <= N < X*Y)
• 接着下面会有N行墙壁的坐标
同一行中如果有多个数据 以一个空格隔开,用例保证所有的输入数据均合法。(结尾不带 回车换行)
三、输出描述
陷阱方格与不可达方格数量,两个信息在一行中输出,以一个空格隔开。(结尾不带回车换行)
四、测试用例
测试用例1:
1、输入
6 4
5
0 2
1 2
2 2
4 1
5 1
2、输出
2 3
3、说明
该输入对应上图示例中的迷宫,陷阱方格有2个,不可达方格有3个
测试用例2:
1、输入
6 4
4
2 0
2 1
3 0
3 1
2、输出
0 4
3、说明
该输入对应的迷宫如下图,没有陷阱方格,不可达方格有4个,分别是(4, 0) (4, 1) (5, 0) (5, 1)
五、解题思路
用两个二维布尔数组做动态规划:
reachable[y][x] 表示从起点(0,0)只向东/北能否到达该格
canReach[y][x] 表示从该格只向东/北能否到达终点(X-1,Y-1),等价于从终点反向只向西/南能否到达该格
算法:
- 正向DP求 reachable
- 反向DP求 canReach
- 统计非墙格:reachable为真且canReach为假 -> 陷阱;reachable为假 -> 不可达
复杂度 O(X*Y),适配 X,Y<=1000。
六、Java算法源码
public class OdTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
if (!sc.hasNextInt()) {
sc.close();
return;
}
int X = sc.nextInt(); // 房间宽度(x轴)
int Y = sc.nextInt(); // 房间高度(y轴)
int N = sc.nextInt(); // 墙壁数量
boolean[][] wall = new boolean[Y][X];
for (int i = 0; i < N; i++) {
int wx = sc.nextInt();
int wy = sc.nextInt();
wall[wy][wx] = true;
}
boolean[][] reachable = new boolean[Y][X];
// 正向DP:从(0,0)向东/北能否到达
for (int y = 0; y < Y; y++) {
for (int x = 0; x < X; x++) {
if (wall[y][x]) {
reachable[y][x] = false;
continue;
}
if (x == 0 && y == 0) {
reachable[y][x] = true; // 起点
} else {
boolean fromLeft = x > 0 && reachable[y][x - 1];
boolean fromDown = y > 0 && reachable[y - 1][x];
reachable[y][x] = fromLeft || fromDown;
}
}
}
boolean[][] canReach = new boolean[Y][X];
// 反向DP:从终点反向向西/南能否到达(等价于正向能到终点)
for (int y = Y - 1; y >= 0; y--) {
for (int x = X - 1; x >= 0; x--) {
if (wall[y][x]) {
canReach[y][x] = false;
continue;
}
if (x == X - 1 && y == Y - 1) {
canReach[y][x] = true; // 终点
} else {
boolean fromRight = x + 1 < X && canReach[y][x + 1];
boolean fromUp = y + 1 < Y && canReach[y + 1][x];
canReach[y][x] = fromRight || fromUp;
}
}
}
int trap = 0;
int unreachable = 0;
for (int y = 0; y < Y; y++) {
for (int x = 0; x < X; x++) {
if (wall[y][x]) {
continue; // 墙不是不可达格
}
if (!reachable[y][x]) {
unreachable++;
} else if (!canReach[y][x]) {
trap++;
}
}
}
System.out.print(trap + " " + unreachable);
sc.close();
}
}
七、效果展示
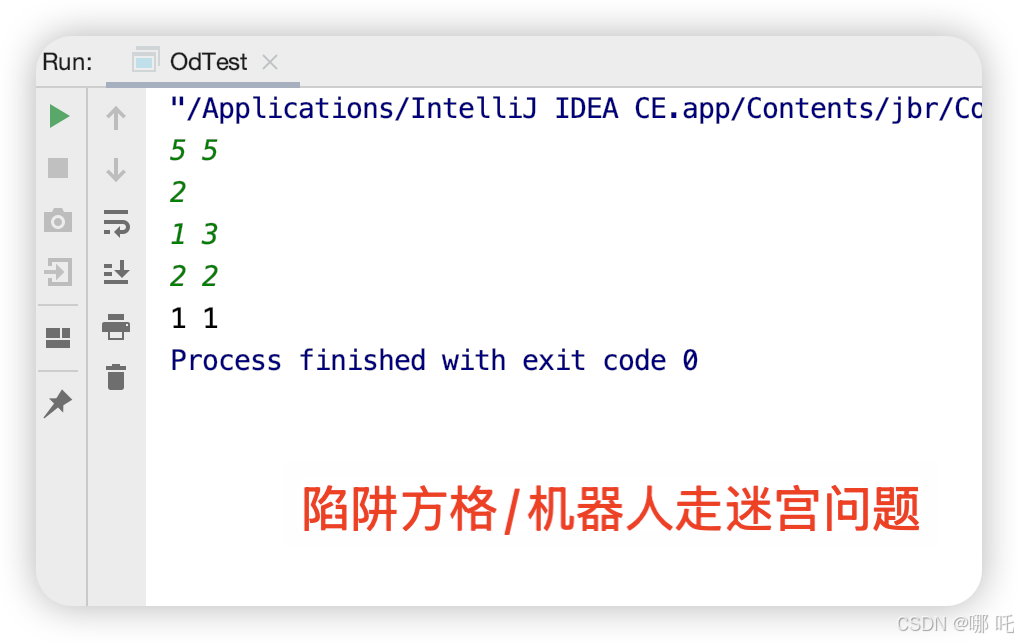
1、输入
5 5
2
1 3
2 2
2、输出
1 1
3、说明
(1,2)可达但无法到出口为陷阱;(2,3)不可达。
🏆下一篇:华为OD机试 - 简易内存池 - 逻辑分析(Java 双机位C卷 200分)
🏆本专栏收录于《华为OD机试(JAVA)真题》。
刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天优快云在线答疑。























 2867
2867

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










