华为OD机试 - 陷阱方格/机器人走迷宫问题 - 动态规划（Python/JS/C/C++ 双机位C卷 200分）

华为OD机试双机位C卷统一考试题库清单（持续收录中）以及考点说明（Python/JS/C/C++）。

专栏导读

本专栏收录于《华为OD机试真题（Python/JS/C/C++）》。

刷的越多，抽中的概率越大，私信哪吒，备注华为OD，加入华为OD刷题交流群，每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景，发现新题目，随时更新。

一、题目描述

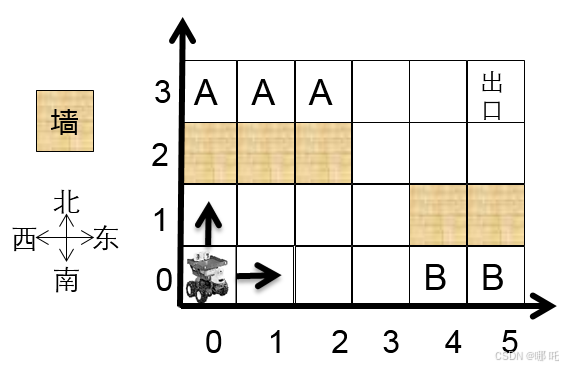
房间由XY的方格组成，例如下图为6*4的大小。每一个方格以坐标(x, y)描述。

机器人固定从方格(0, 0)出发，只能向东或者向北前进。出口固定为房间的最东北角，如下图的方格(5, 3)。用例保证机器人可以从入口走到出口。

房间有些方格是墙壁，如(4, 1)，机器人不能经过那儿。

有些地方是一旦到达就无法走到出口的，如标记为B的方格，称之为陷阱方格。

有些地方是机器人无法到达的，如标记为A的方格，称之为不可达方格，不可达方格不包括墙壁所在的位置。

如下示例图中，陷阱方格有2个，不可达方格有3个。

请为该机器人实现路径规划功能：给定房间大小、墙壁位置，请计算出陷阱方格与不可达方格分别有多少个。

二、输入描述

第一行为房间的X和Y（0 < X,Y <= 1000）

• 第二行为房间中墙壁的个数N（0 <= N < X*Y）

• 接着下面会有N行墙壁的坐标

同一行中如果有多个数据 以一个空格隔开，用例保证所有的输入数据均合法。（结尾不带 回车换行）

三、输出描述

陷阱方格与不可达方格数量，两个信息在一行中输出，以一个空格隔开。（结尾不带回车换行）

四、测试用例

测试用例1：

1、输入

6 4
5
0 2
1 2
2 2
4 1
5 1

2、输出

2 3

3、说明

该输入对应上图示例中的迷宫，陷阱方格有2个，不可达方格有3个

测试用例2：

1、输入

6 4
4
2 0
2 1
3 0
3 1

2、输出

0 4

3、说明

该输入对应的迷宫如下图，没有陷阱方格，不可达方格有4个，分别是(4, 0) (4, 1) (5, 0) (5, 1)

五、解题思路

用两个二维布尔数组做动态规划：

reachable[y][x] 表示从起点(0,0)只向东/北能否到达该格

canReach[y][x] 表示从该格只向东/北能否到达终点(X-1,Y-1)，等价于从终点反向只向西/南能否到达该格

算法：

1. 正向DP求 reachable
2. 反向DP求 canReach
3. 统计非墙格：reachable为真且canReach为假 -> 陷阱；reachable为假 -> 不可达
   复杂度 O(X*Y)，适配 X,Y<=1000。

六、Python算法源码

import sys

def main():
    data = sys.stdin.read().strip().split()
    if not data:
        return
    it = iter(data)
    X = int(next(it))
    Y = int(next(it))
    N = int(next(it))

    wall = [[False] * X for _ in range(Y)]
    for _ in range(N):
        wx = int(next(it))
        wy = int(next(it))
        wall[wy][wx] = True

    reachable = [[False] * X for _ in range(Y)]
    # 正向DP：从起点只向东/北能否到达
    for y in range(Y):
        for x in range(X):
            if wall[y][x]:
                continue
            if x == 0 and y == 0:
                reachable[y][x] = True
            else:
                from_left = x > 0 and reachable[y][x - 1]
                from_down = y > 0 and reachable[y - 1][x]
                reachable[y][x] = from_left or from_down

    can_reach = [[False] * X for _ in range(Y)]
    # 反向DP：从终点反向向西/南能否到达
    for y in range(Y - 1, -1, -1):
        for x in range(X - 1, -1, -1):
            if wall[y][x]:
                continue
            if x == X - 1 and y == Y - 1:
                can_reach[y][x] = True
            else:
                from_right = x + 1 < X and can_reach[y][x + 1]
                from_up = y + 1 < Y and can_reach[y + 1][x]
                can_reach[y][x] = from_right or from_up

    trap = 0
    unreachable = 0
    for y in range(Y):
        for x in range(X):
            if wall[y][x]:
                continue
            if not reachable[y][x]:
                unreachable += 1
            elif not can_reach[y][x]:
                trap += 1

    sys.stdout.write(f"{trap} {unreachable}")

if __name__ == "__main__":
    main()

七、JavaScript算法源码

const fs = require('fs');

const input = fs.readFileSync(0, 'utf8').trim();
if (input.length === 0) process.exit(0);
const data = input.split(/\s+/).map(Number);
let idx = 0;

const X = data[idx++];
const Y = data[idx++];
const N = data[idx++];

const wall = Array.from({ length: Y }, () => Array(X).fill(false));
for (let i = 0; i < N; i++) {
    const wx = data[idx++];
    const wy = data[idx++];
    wall[wy][wx] = true;
}

const reachable = Array.from({ length: Y }, () => Array(X).fill(false));
// 正向DP：从起点只向东/北能否到达
for (let y = 0; y < Y; y++) {
    for (let x = 0; x < X; x++) {
        if (wall[y][x]) continue;
        if (x === 0 && y === 0) {
            reachable[y][x] = true;
        } else {
            const fromLeft = x > 0 && reachable[y][x - 1];
            const fromDown = y > 0 && reachable[y - 1][x];
            reachable[y][x] = fromLeft || fromDown;
        }
    }
}

const canReach = Array.from({ length: Y }, () => Array(X).fill(false));
// 反向DP：从终点反向向西/南能否到达
for (let y = Y - 1; y >= 0; y--) {
    for (let x = X - 1; x >= 0; x--) {
        if (wall[y][x]) continue;
        if (x === X - 1 && y === Y - 1) {
            canReach[y][x] = true;
        } else {
            const fromRight = x + 1 < X && canReach[y][x + 1];
            const fromUp = y + 1 < Y && canReach[y + 1][x];
            canReach[y][x] = fromRight || fromUp;
        }
    }
}

let trap = 0;
let unreachable = 0;
for (let y = 0; y < Y; y++) {
    for (let x = 0; x < X; x++) {
        if (wall[y][x]) continue;
        if (!reachable[y][x]) {
            unreachable++;
        } else if (!canReach[y][x]) {
            trap++;
        }
    }
}

process.stdout.write(`${trap} ${unreachable}`);

八、C算法源码

#include <stdio.h>
#include <stdlib.h>

int main() {
    int X, Y;
    if (scanf("%d %d", &X, &Y) != 2) return 0;
    int N;
    scanf("%d", &N);

    int size = X * Y;
    // 使用一维数组模拟二维
    char *wall = (char *)calloc(size, sizeof(char));
    char *reachable = (char *)calloc(size, sizeof(char));
    char *canReach = (char *)calloc(size, sizeof(char));

    for (int i = 0; i < N; i++) {
        int wx, wy;
        scanf("%d %d", &wx, &wy);
        wall[wy * X + wx] = 1;
    }

    // 正向DP：从起点只向东/北能否到达
    for (int y = 0; y < Y; y++) {
        for (int x = 0; x < X; x++) {
            int idx = y * X + x;
            if (wall[idx]) continue;
            if (x == 0 && y == 0) {
                reachable[idx] = 1;
            } else {
                int fromLeft = (x > 0) && reachable[y * X + (x - 1)];
                int fromDown = (y > 0) && reachable[(y - 1) * X + x];
                reachable[idx] = (fromLeft || fromDown) ? 1 : 0;
            }
        }
    }

    // 反向DP：从终点反向向西/南能否到达
    for (int y = Y - 1; y >= 0; y--) {
        for (int x = X - 1; x >= 0; x--) {
            int idx = y * X + x;
            if (wall[idx]) continue;
            if (x == X - 1 && y == Y - 1) {
                canReach[idx] = 1;
            } else {
                int fromRight = (x + 1 < X) && canReach[y * X + (x + 1)];
                int fromUp = (y + 1 < Y) && canReach[(y + 1) * X + x];
                canReach[idx] = (fromRight || fromUp) ? 1 : 0;
            }
        }
    }

    int trap = 0, unreachable = 0;
    for (int y = 0; y < Y; y++) {
        for (int x = 0; x < X; x++) {
            int idx = y * X + x;
            if (wall[idx]) continue;
            if (!reachable[idx]) {
                unreachable++;
            } else if (!canReach[idx]) {
                trap++;
            }
        }
    }

    printf("%d %d", trap, unreachable);

    free(wall);
    free(reachable);
    free(canReach);
    return 0;
}

九、C++算法源码

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int X, Y;
    if (!(cin >> X >> Y)) return 0;
    int N;
    cin >> N;

    vector<vector<bool>> wall(Y, vector<bool>(X, false));
    for (int i = 0; i < N; i++) {
        int wx, wy;
        cin >> wx >> wy;
        wall[wy][wx] = true;
    }

    vector<vector<bool>> reachable(Y, vector<bool>(X, false));
    // 正向DP：从起点只向东/北能否到达
    for (int y = 0; y < Y; y++) {
        for (int x = 0; x < X; x++) {
            if (wall[y][x]) continue;
            if (x == 0 && y == 0) {
                reachable[y][x] = true;
            } else {
                bool fromLeft = x > 0 && reachable[y][x - 1];
                bool fromDown = y > 0 && reachable[y - 1][x];
                reachable[y][x] = fromLeft || fromDown;
            }
        }
    }

    vector<vector<bool>> canReach(Y, vector<bool>(X, false));
    // 反向DP：从终点反向向西/南能否到达
    for (int y = Y - 1; y >= 0; y--) {
        for (int x = X - 1; x >= 0; x--) {
            if (wall[y][x]) continue;
            if (x == X - 1 && y == Y - 1) {
                canReach[y][x] = true;
            } else {
                bool fromRight = x + 1 < X && canReach[y][x + 1];
                bool fromUp = y + 1 < Y && canReach[y + 1][x];
                canReach[y][x] = fromRight || fromUp;
            }
        }
    }

    int trap = 0, unreachable = 0;
    for (int y = 0; y < Y; y++) {
        for (int x = 0; x < X; x++) {
            if (wall[y][x]) continue;
            if (!reachable[y][x]) {
                unreachable++;
            } else if (!canReach[y][x]) {
                trap++;
            }
        }
    }

    cout << trap << " " << unreachable;
    return 0;
}

🏆下一篇：华为OD机试真题 - 简易内存池（Python/JS/C/C++ 双机位C卷 200分）

🏆本文收录于，华为OD机试真题（Python/JS/C/C++）

刷的越多，抽中的概率越大，私信哪吒，备注华为OD，加入华为OD刷题交流群，每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景，发现新题目，随时更新。