USACO历年青铜组真题解析 | 2017年12月Blocked Billboard

欢迎大家订阅我的专栏：算法题解：C++与Python实现！
本专栏旨在帮助大家从基础到进阶 ，逐步提升编程能力，助力信息学竞赛备战！

专栏特色
1.经典算法练习：根据信息学竞赛大纲，精心挑选经典算法题目，提供清晰的代码实现与详细指导，帮助您夯实算法基础。
2.系统化学习路径：按照算法类别和难度分级，从基础到进阶，循序渐进，帮助您全面提升编程能力与算法思维。

适合人群：

• 准备参加蓝桥杯、GESP、CSP-J、CSP-S等信息学竞赛的学生
• 希望系统学习C++/Python编程的初学者
• 想要提升算法与编程能力的编程爱好者

附上汇总贴：USACO历年青铜组真题解析 | 汇总-优快云博客

---

【题目描述】

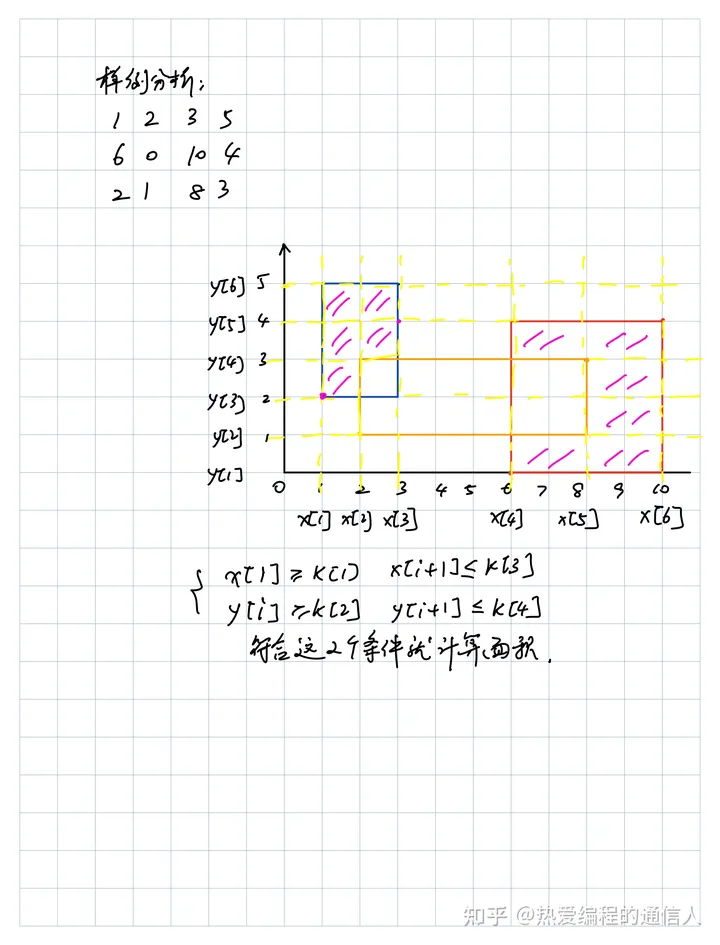
在平面直角坐标系中，有两个矩形（保证不相交），然后给出第三个矩形，求这两个矩形没有被第三个矩形遮住的部分的面积。

【输入】

题目给出三个坐标，分别表示三个矩形的左下、右上坐标

【输出】

Please output the total combined area of both billboards that remains visible.

【输入样例】

1 2 3 5
6 0 10 4
2 1 8 3

【输出样例】

17

【代码详解】

// 使用离散化方法求解
#include <bits/stdc++.h>
using namespace std;
int a[5], b[5], c[5], ans=0;
int x[7], y[7];
bool in(int i, int j, int k[])  // 判断任一坐标是否在矩阵内
{
    if (x[i]>=k[1] && x[i+1]<=k[3] && y[j]>=k[2] && y[j+1]<=k[4]) {  // 满足大于左下，小于右上的坐标就属于在矩阵内
        return true;
    }
    return false;  // 否则返回false
}
int main()
{
    for (int i=1; i<=4; i++) {  // 输入矩阵a的坐标
        cin >> a[i];
    }    
    for (int i=1; i<=4; i++) {  // 输入矩阵b的坐标
        cin >> b[i];
    }    
    for (int i=1; i<=4; i++) {  // 输入矩阵c的坐标
        cin >> c[i];
    }    
    x[1]=a[1], x[2]=a[3], x[3]=b[1], x[4]=b[3], x[5]=c[1], x[6]=c[3];  // 将x轴坐标提出来放到x数组中
    y[1]=a[2], y[2]=a[4], y[3]=b[2], y[4]=b[4], y[5]=c[2], y[6]=c[4];  // 将y轴坐标提出来放到y数组中
    sort(x+1, x+6+1);  // 对x和y数组按照从小到大方式排序
    sort(y+1, y+6+1);
    for (int i=1; i<=5; i++) {  // 一共6个坐标，共5条线段，所以遍历5*5的矩阵
        for (int j=1; j<=5; j++) {
            if (in(i, j, a) && !in(i, j, c) || in(i, j, b) && !in(i, j, c)) {  // 判断任一点坐标在a不再c中，在b不再c中，符合条件的就算
                ans += (y[j+1]-y[j])*(x[i+1]-x[i]);  // 就计算矩阵的面积，并进行累加
            }
        }
    }
    cout << ans << endl;  // 打印结果
    return 0;
}

【运行结果】

1 2 3 5
6 0 10 4
2 1 8 3
17