1. z-score 标准化
x-μ只改变均值,标准差不变,所以均值变为0
(x-μ)/σ只会使标准差除以σ倍,所以标准差变为1

2. 方差 vs 标准差
方差: 衡量随机变量或一组数据时离散程度的度量。
标准差: 衡量随机变量或一组数据时离散程度的度量。
so why 方差和标准差同时存在?答:量纲不同,方差与我们要处理的数据的量纲是不一致的,虽然能很好的描述数据与均值的偏离程度,但是处理结果是不符合我们的直观思维。
举例:
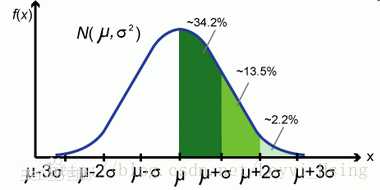
一个班级里有60个学生,平均成绩是70分,标准差是9,方差是81,成绩服从正态分布,那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分,通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为0.6826,即约等于下图中的34.2%*2
3. 标准差(均方差)vs 均方根误差
均方差(标准差)是数据序列与均值的关系,而均方根误差是数据序列与真实值之间的关系。
因此,标准差是用来衡量一组数自身的离散程度,而均方根误差是用来衡量观测值同真值之间的偏差,它们的研究对象和研究目的不同,但是计算过程类似。
4. 协方差
协方差为0时,两者独立。协方差绝对值越大,两者对彼此的影响越大,反之越小。
5. 多项分布:
举个例子,投k次色子,可能发生的情况是1--6,对应{},以及假设发生这六种情况的可能性分别为{
}(可能色子六个面不均匀所以可能性不一定全相等),发生这六种情况得次数为{
}
, 则联合分布:
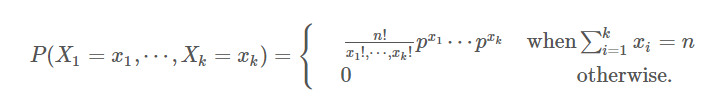




















 2450
2450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








