接雨水问题总结

力扣 84 题 如下：

【解法一】暴力法
解题思路：每根主子的存水量 = 该柱子的左右两侧最大高度的较小者减去此柱子的高度。只要能找到每根柱子的左右两侧的最大值就能求出当前柱子的接水量。
代码如下

	/**
	 * 暴力破解法：
	 * 每根主子的存水量 = 该柱子的左右两侧最大高度的较小者减去此柱子的高度。
	 */
	public static int solution(int[] height){
		int res = 0;
		// 遍历每个柱子
		for (int i = 1; i < height.length - 1; i++) {
			int leftMax = 0, rightMax = 0;// 最大值要每次for循环刷新，不能定义到for外面
			// 计算当前柱子左侧的柱子中的最大高度
			// 在求左侧和右侧最大值时 需要有等号，如果比较当前值height[j],可能会有左右两侧的值最大值都小于当前值，
			// 在求蓄水高度时Math.min(leftMax, rightMax) - height[i] 就有可能会产生负值，
			// 如果比较了当前值，那么左侧 和右侧的最大值 一定时 ≥ height[i]，这样求蓄水值 Math.min(leftMax, rightMax) - height[i] 为零，不会为负值
			for (int j = 0; j <= i; j++) {
				leftMax = Math.max(leftMax, height[j]);
			}
			// 计算当前柱子右侧的柱子中的最大高度
			for (int j = i; j < height.length; j++) {
				rightMax = Math.max(rightMax, height[j]);
			}
			// 结果中累加当前柱子顶部可以储水的高度，
			// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
			res += Math.min(leftMax, rightMax) - height[i];
		}
		return res;
		
	}

【解法二】 动态规划
在上述的暴力法中，对于每个柱子，我们都需要从两头重新遍历一遍求出左右两侧的最大高度，这里是有很多重复计算的，
很明显最大高度是可以记忆化的，具体在这里可以用数组边递推边存储，也就是常说的动态规划，DP。
具体做法：定义二维dp数组 int[][] dp = new int[n][2]，其中，
  dp[i][0] 表示下标i的柱子左边的最大值，
  dp[i][1] 表示下标i的柱子右边的最大值。
分别从两头遍历height数组，为 dp[i][0]和 dp[i][1] 赋值。
同方法1，遍历每个柱子，累加每个柱子可以储水的高度

代码如下

public static int solution2(int[] height){
		int n = height.length;
		if (n == 0) {
			return 0;
		}
		int res = 0;
		// 定义二维dp数组
        // dp[i][0] 表示下标i的柱子左边的最大值
        // dp[i][1] 表示下标i的柱子右边的最大值
		int[][] dp = new int[n][2];
		dp[0][0] = height[0];
		dp[n-1][1] = height[n-1];
		for (int i = 1; i < n; i++) {
			dp[i][0] = Math.max(dp[i - 1][0], height[i]);// 把当前遍历值与左侧前i-1个值最大值比较
		}

		for (int i = n - 2; i >= 0; i--) {
			dp[i][1] = Math.max(dp[i + 1][1], height[i]);
		}
		for (int i = 0; i < n; i++) {
			res += Math.min(dp[i][0], dp[i][1]) - height[i];
		}
		return res;
	}

【解法三】 双指针法
对方案二 动态规划的空间上的优化（感觉有点取巧了呀！！！个人想破脑袋估计是也想不到......）
每根柱子的接水量 = 左右两侧柱子最大值的较小值 - 当前柱子。
设左侧最大值为 l_max  右侧最大值为 r_max-
当前  i 处左边的最大值如果比右边最大值要的小，那么就可以不用考虑  i 处右边最大值的影响了，因为 i 处接水量由左右两侧较小值决定的。
 如果左侧最大值   <  右侧最大值  雨水量由左侧最大值决定 
         此时可以确定左侧指针指向柱子处的接水量，右侧指针的柱子接水量不能确定
如果左侧最大值   ≥  右侧最大值  雨水量由右侧最大值决定
        此时可以确定右侧指针指向柱子处的接水量，左侧指针的柱子接水量不能确定

代码如下

public static int solution3(int[] height){
		int n = height.length;
		if (n == 0) {
			return 0;
		}
		int res = 0;
		int left = 0, right = n - 1;
		int l_max = height[0], r_max = height[n-1];
		while(left <= right){
			if (l_max < r_max) {// 左边最大值  < 右边最大值   可以确定左指针处柱子的积水量，右指针处柱子接水量无法确定
				if (l_max > height[left]) {
					res += l_max-height[left];// 计算左指针指向的柱子的积水量，右侧指针处柱子不动
				}else{
					l_max = height[left];// 更新左侧最大值
				}
				left++;// 移动左侧指针，右指针不动
			} else{// 左边最大值 ≥ 右边最大值  可以确定右指针处柱子的积水量，左指针处柱子接水量无法确定
				if(r_max > height[right]){
					res += r_max - height[right];// 计算右指针指向的柱子的积水量，左侧侧指针处柱子不动
				}else{
					r_max = height[right];// 更新右侧最大值
				}
				right--;// 移动右指针，左指针不动
			}
		}
		return res;
	}

        /**
	 * 双指针法   代码简化版
	 * 
	 */
	public static int solution4(int[] height){
		int n = height.length;
		if (n == 0) {
			return 0;
		}
		int res = 0;
		int left = 0, right = n - 1;
		int l_max = height[0], r_max = height[n-1];
		while(left <= right){
			if (l_max < r_max) {// 左边最大值  < 右边最大值   可以确定左指针处柱子的积水量，右指针处柱子接水量无法确定
				l_max = Math.max(l_max, height[left]);
				res += l_max-height[left];// 计算左指针指向的柱子的积水量，右侧指针处柱子不动
				left++;// 移动左侧指针，右指针不动
			} else{// 左边最大值 ≥ 右边最大值  可以确定右指针处柱子的积水量，左指针处柱子接水量无法确定
				r_max = Math.max(r_max, height[right]);
				res += r_max - height[right];// 计算右指针指向的柱子的积水量，左侧侧指针处柱子不动
				right--;// 移动右指针，左指针不动
			}
		}
		return res;
	}

【解法三】 单调栈
使用单调递增栈来计算接水量，只有形成凹槽时才能接水，单调栈求接水量时一层一层的计算的，与前三种方案不同（前三种方案按照每根柱子单独来求节水量），单调栈是横向的求积水面积，而动态规划及双指针是纵向的的求接水量。
单调栈求解接水量需要注意两个地方

1. 只有形成凹槽时才能积水，我们可以使用单调增栈来存储遍历的数据，栈中数据从栈底到栈顶依次递减，出栈时数据依次递增，形成凹槽时，必须要当前遍历值与栈顶元素形成反差，即当前遍历值大于栈顶元素，弹出栈顶元素后，栈中依然有数据(不为空)，则可以形成凹槽。如第二个 1 入栈时与栈顶元素 0形成反差，弹出栈顶元素 0 后，栈中依然有数据 1，则可以形成凹槽，如果栈中数据为空，说明弹出的栈顶的元素左侧没有比它要大的数据，不能形成凹槽，就不能接水。
   
   
   
   
    
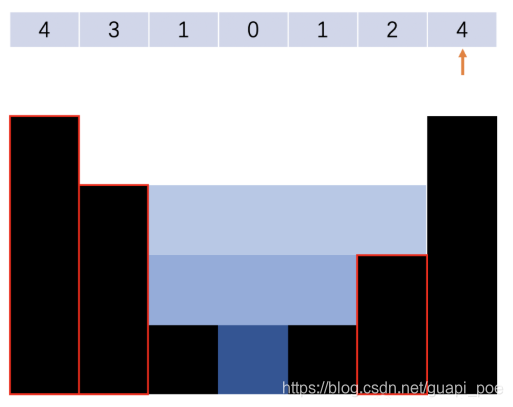
2. 因为我们求积水是一层一层的横向的计算的，当出现相同值情况，如下 2 入栈时，栈中从栈底到栈顶依次为  4  3  1  1 ，我们需要将两个 1 同时弹出，如下图求绿色区域的积水量，即我们需要将所有相同值全部弹出，然后再求横向的绿色区域积水量。

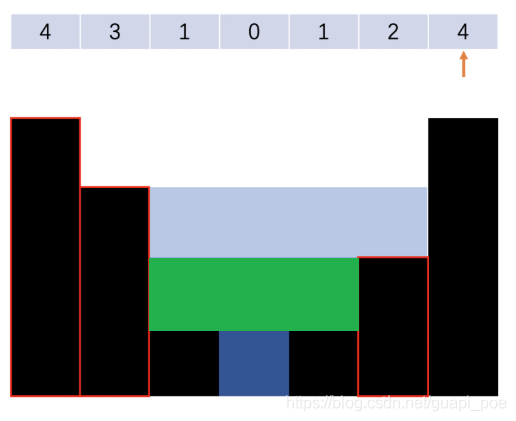
     3.凹槽积水量的计算，遇到凹槽时即违反单调栈递减规律时，弹出栈顶元素，我们计算弹出的栈顶元素的接水量时，需要将当          前值与栈顶元素比较取较小值来形成积水的高度，如下图两种情况：绿色区域的积水量与两侧柱子高度较小值有关。

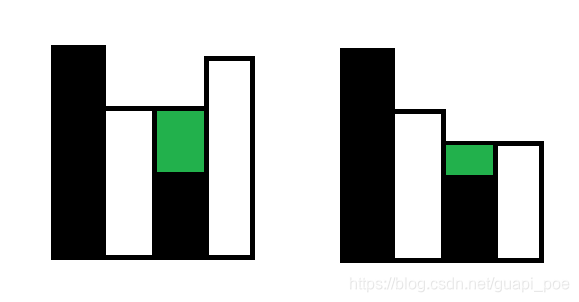
代码如下

public static int solution5(int[] height){
		int res = 0;
		Deque<Integer> stack = new ArrayDeque<>();
		for (int i = 0; i < height.length; i++) {
			while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
				int top = stack.pop();
				while (!stack.isEmpty() && height[top] == height[stack.peek()]) {
					stack.pop();// 需要考虑重复元素
				}
				if (!stack.isEmpty()) {
					int min = Math.min(height[i], height[stack.peek()]);// 取当前遍历值 与 栈顶元素的较小值
					res += (min - height[top]) * (i - stack.peek() - 1);
				}

			}
			stack.push(i);
		}
		return res;
	}

后记

接雨水问题到此全部的解法已全部搞定，算法练习刚刚起步，跟大佬差距还是蛮大的呀，努力呀还得。。。。