基于ASQVD与边匹配的隐写术

5 基于加减的QVD和边匹配的图像隐写术

5.1 引言

近年来，互联网已成为数据通信的首选媒介。然而，互联网传输的数据面临着安全挑战。因此，密码学和隐写术等技术引起了研究人员的关注。隐写术通过将数据隐藏在其他文件（如图像、视频和音频）中来保障数据的安全性[1]在图像中进行数据隐藏时，应不改变其固有属性，以使图像看起来无害[2]自数字图像隐写术问世以来，研究人员一直通过修改最低有效位（LSB）来在图像中隐藏数据。但这种方法容易被正则‐奇异（RS）测试检测到[3]图像中的一种流行隐写方案是像素值差分（PVD），该方法由吴和蔡提出[4]在此方案中，一个 1×2大小像素块内两个像素值之间的差值决定了该块的数据隐藏容量（HC）。但此方案可被像素差分直方图（PDH）测试所检测[5]通过在 2 × 2和 3× 3大小的块中使用PVD隐写术， HC得到了进一步提升[6–8]。

在吴和蔡最初的PVD中，每个像素块都使用一个固定且预定义的范围表。罗等人[9]使范围表具有自适应性，并使用了 1× 3大小的块。目标像素中的隐藏容量（HC）取决于其下界（LB）和上界（UB）。其LB和UB值是从块中的其他像素导出的。因此，该范围表是自适应的。这种自适应PVD概念已被进一步扩展到 2× 2和 3× 3大小的块，以隐藏更多的数据量[10]。普拉丹等人[11]使用 2× 3和 3× 2大小的像素块，相较于 2× 2和 3× 3大小的块获得了更好的结果。这些方案的隐藏容量（HC）小于传统PVD方案的隐藏容量（HC）。此外，还提出了基于PVD的自适应LSB修改隐写术[12,13]。在这些技术中，利用PVD概念来确定块中像素的隐藏容量（HC），并据此决定使用多少个最低有效位来隐藏数据。

Wu等人[14]认为，在纹理区域应用PVD，在非纹理区域应用LSB替换，可以降低失真，同时提高隐藏容量。Yang等人[15]指出，Wu等人的方案将大多数块分类为平滑类别，而较少数量的块被分类为纹理类别。因此，主要执行的是最低有效位替换数字媒体隐写术。htt p s://doi.or g /10.1016/B978-0-12-819438-6.00013-X版权所有© 2020爱思唯尔公司保留所有权利。

81
82 数字媒体 隐写术

大多数块，因此RS分析可以检测到它。霍达伊与法兹 [16]利用 1 × 3大小的像素块，对中心像素进行LSB替换，对其两个相邻像素进行PVD处理。该技术可被PDH检测发现，并受越界问题（FOBP）影响。斯温 [17]提出了一种改进版本的技术，使用 2× 2大小的像素块以获得更高的隐藏容量。

王等人[18]提出了基于模函数的差值扩展（MFPVD），其中他们使用余数值代替差值。
赵等人[19]提出了该方法的改进版本。斯温[20]证明了王等人的技术存在范围不匹配问题，此外，他在 2 × 3大小的像素块中提出了一种改进版本，并成功避免了范围不匹配问题。杨等人[21]在 2× 2大小的像素块中进行了水平、垂直和对角配对，并在不同合适的方向上应用PVD，实现了更低失真下的更高隐藏容量。普拉丹等人[22]将图像块分为两类：（i）边缘区域和（ii）平滑区域。他们在边缘区域应用PVD与LSB替换相结合的方法，而在平滑区域则采用利用修改方向（EMD）与LSB替换相结合的方法。

唐等人[23]认为，在使用彩色像素的三个通道时，这三个通道应全部为正向取向或全部为负向取向，以保持三个通道之间的统计相关性。李等人[24]也认为，为了提高安全性，图像中高纹理区域的像素值应朝同一方向进行修改。数据隐藏技术有许多实际应用。已有研究指出，隐写术可用于基于物联网的应用中传输医疗数据[25]。隐写术还可应用于社交网络中的一批图像来隐藏数据[26]。

郑[27]从一个 1× 2大小的像素块中提取了高位平面和低位平面，然后在低位平面中应用最低有效位修改，在高位平面中应用差值扩展方法。高位平面由六个最高有效位（MSB）组成，低位平面由两个最低有效位（LSBs）组成。最后，在嵌入完成后，将低位平面和高位平面合并形成一个隐写块。斯温[28]通过案例研究指出郑方案存在首比特翻转问题，并使用 3 × 3块开发了一个改进版本。该改进方案避免了首比特翻转问题，并且能够抵抗RS检测和 PDH检测。普拉丹等人[7]将吴与蔡的差值扩展方法扩展到多个方向，使用 3× 3块进行处理。

但其隐藏容量仅为2.39每字节比特数（BPB）。斯温[29]将霍达伊与法兹的技术扩展到 3× 3大小的块，从而获得了相对更好的性能并增强了对PDH分析的防护能力。

刘等人 [30]提出了一种在 3×3大小的像素块中的隐写方案。他们将PVD应用于中心像素及其左、右、上和下相邻像素。在获得这些像素的隐写值后，他们采用边匹配方法在块中剩余的四个角像素中进行嵌入。哈米德等人 [31]提出了一种在 2× 2大小的像素块中的隐写方法，通过为RGB图像中每个颜色通道选择合适的隐藏方向，以实现最大的隐藏容量。由于在不同通道中动态使用不同的嵌入方向来隐藏可变数量的数据位，安全性得到了提高。萨胡和斯温 [32]提出了一种隐写技术，其中像素的隐写值取决于载体图像像素的 n‐最低有效位的十进制值以及

章 5 •基于加减QVD和边匹配的图像隐写术 83

秘密数据位的十进制值。它不存在首比特翻转问题，并具有更高的嵌入容量。萨胡和斯温 [33]提出了一种基于双隐写图像的嵌入新隐写方案，该方案从原始图像生成两幅镜像，然后使用LSB匹配将数据隐藏在这些图像中。尽管其嵌入容量并未显著提高，但该方案具有可逆性。

一般来说，PVD技术存在首比特翻转问题（FOBP）以及易被PDH检测发现等问题。为解决这些问题，本文结合了基于加减的商值差分（ASQVD）和边匹配（SM）原理。该方法实现了平均隐藏容量（HC）为3.55每字节比特数（BPB），平均峰值信噪比（PSNR）为 33.89分贝（dB）。此外，RS检测和PDH检测均无法追踪到这种隐写术。

5.2 提出的ASQVD+SM技术

5.2.1 嵌入过程

原始图像的像素进行光栅扫描，并被逻辑地划分为 3 × 3个不相交的像素块，参见图5.1A。
该块上的嵌入操作分两个阶段进行：(i)第一阶段和(ii)第二阶段。第一阶段执行ASQVD和余数替换，第二阶段执行边匹配嵌入。

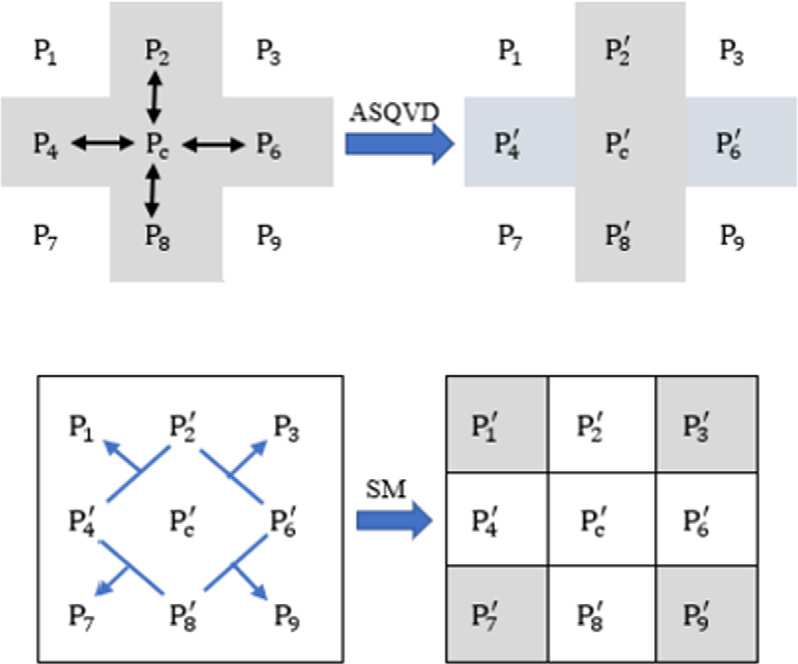
第一阶段的嵌入过程对像素Pc、P2, P4, P6,和P8应用ASQVD。该过程在步骤1至8中进行描述。

步骤1： Pc是块中的中心像素。其上下左右相邻像素分别是P2,、P4,、P6,和P8,。对Pc应用4位LSB替换，得到其隐写值P′ c。

84 数字媒体 隐写术

步骤2： 设decold表示Pc的四个最低有效位，decnew表示P′c的四个最低有效位。现在确定变化量 var = decold−decnew，并按照公式(5.1)计算P′c的修改值。此过程称为4位改进型最低有效位 (MLSB)替换。

$$
P′c=
\begin{cases}
P′c+ 2^4 & \text{if } var> 2^3 \text{ and } 0 ≤ P′c+ 2^4 ≤255, \
P′c −2^4 & \text{if var< −2^3 \text{ and } 0 ≤ P′c −2^4 ≤255, \
P′c & \text{otherwise.}
\end{cases}
\quad (5.1)
$$

步骤3： 从像素 P′c, P2, P4, P6,和 P8中，分别使用公式(5.2)和公式(5.3)计算商和余数。

$$
Q′c= P′c \div 4, \quad \text{and} \quad Qi= Pi \div 4 \quad \text{for } i= 2,4,6,8; \quad (5.2)
$$
$$
R′c= P′c \mod 4, \quad \text{and} \quad Ri= Pi \mod 4 \quad \text{for } i= 2,4,6,8. \quad (5.3)
$$

步骤4: 利用Q′c和Qi代入公式(5.4)以确定四个差值

$$
di= |Q′c −Qi| \quad \text{for } i= 2,4,6,8. \quad (5.4)
$$

对于 i = 2,4,6,8, di属于表 5.1 的范围。设 Li和 ti分别表示该范围的低边界和隐藏容量。对于 i = 2,4,6,8, 确定 Si，即 ti个秘密位的十进制值。

表5.1 所提ASQVD技术的范围表。

像素差值范围	{0,7}	{8,15}	{16,31}	{32,63}
范围容量	2	2	3	3

步骤5: 利用公式(5.5)确定d′ i,的新值i：

$$
d′ i= Li+ Si \quad \text{for } i= 2,4,6,8. \quad (5.5)
$$

步骤6: 对于每个商值Qi，计算Q′′ i和Q′′′ i，使用公式(5.6)并根据公式(5.7)确定Q′ i：

$$
Q′′ i= Q′ c − d′ i \quad \text{and} \quad Q′′′ i= Q′ c+ d′ i \quad \text{for } i= 2,4,6,8; \quad (5.6)
$$

$$
Q′ i=
\begin{cases}
Q′′ i & \text{if}(Q′′′ i> 63) \text{ or }((0 ≤ Q′′ i ≤63) \text{ and }(0 ≤ Q′′′ i ≤63) \text{ and }(|Qi −Q′′ i| ≤|Qi −Q′′′ i|)), \
Q′′′ i & \text{if}(Q′′ i < 0) \text{ or }((0 ≤ Q′′ i ≤63) \text{ and }(0 ≤Q′′′ i ≤63) \text{ and }(|Qi −Q′′′ i| < |Qi −Q′′ i|)),
\end{cases}
\quad \text{for } i= 2,4,6,8.
\quad (5.7)
$$

步骤7: 对于每个余数 R2, R4, R6,和 R8,，需要找到它们的隐写值。对于 i = 2,4,6,8，确定 R′ i ,，即对应 2 个秘密比特的十进制数字。假设 R′ i是 Ri的隐写值。

第 5 •基于加减QVD和边匹配的图像隐写术 85

步骤8: 利用公式(5.8)，确定 P′i,的隐写值 Pi：

$$
P′i= Q′i × 4+ R′i \quad \text{for } i= 2,4,6,8. \quad (5.8)
$$

通过这种方式，我们将数据隐藏在像素 Pc、P2,、P4,、P6, 和 P8 中（见图 5.2）。

应用上述步骤后，原始块被转换为中间隐写块；见图5.1B。

阶段2 的嵌入过程在像素P1, P3, P7,和P9上应用SM方法。图5.1C表示这些像素中的每一个的两个侧像素。步骤9–12描述了嵌入过程的第二阶段。

步骤9: 像素P1的两个相邻像素是P′2和P′4。类似地，像素P3的两个相邻像素是P′2和P′6。像素P7的两个相邻像素是P′4和P′8。像素P9的两个相邻像素是P′6和P′8。使用公式(5.9)计算四个差值d1,、d3,、d7,和d9：

$$
d1= |P′2 − P′4|, \quad d3= |P′2 − P′6|, \quad d7= |P′4 − P′8|, \quad d9= |P′6 − P′8|. \quad (5.9)
$$

步骤10: 对于 i = 1,3,7,9，使用公式(5.10)计算 ni。如果 ni ≥4，则设置 ni= 4。

$$
ni=
\begin{cases}
1 & \text{if } 0 ≤ di ≤1, \
\lfloor \log_2 di \rfloor & \text{if } di> 1.
\end{cases}
\quad (5.10)
$$

步骤11: 对于 i = 1,3,7,9，确定 bi，即 ni个秘密位的十进制值。在将 bi嵌入 Pi后，使用公式(5.11)计算隐写值 P′ i。

$$
P′ i= Pi −Pi \mod 2^{ni}+ bi. \quad (5.11)
$$

步骤12: 对于 i = 1,3,7,9，计算差值 i= P′ i − Pi。应用公式(5.12)对 P′ i进行进一步调整。

$$
P′ i=
\begin{cases}
P′ i −2^{ni} & \text{if}(2^{ni−1}<i< 2^{ni}) \text{ and }(P′ i ≥2^{ni}), \
P′ i+ 2^{ni} & \text{if}(−2^{ni}< i< −2^{ni−1 }) \text{ and }(P′ i ≤255 −2^{ni}).
\end{cases}
\quad (5.12)
$$

应用步骤9–12后，我们得到最终隐写块；参见图 5.1D。

5.2.2 提取过程

与嵌入过程类似，隐写图像被分割为 3 × 3大小的像素块，如图 5.1D所示。从此块中分两个阶段进行数据提取，(i) 第一阶段 和 (ii) 第二阶段。

第一阶段 提取过程应用于像素 P′ c, P′ 2 , P′ 4 , P′ 6 ,和 P′ 8。该过程在步骤1–4中执行。

86 数字媒体隐写术

第 5 •基于加减QVD和边匹配的图像隐写术 87

步骤1: 提取 P 的 4 个最低有效位′c并将其保留在提取的二进制数据流 (EBDS) 中。对于 i = 2, 4,6,8, 使用公式 (5.13) 确定 P′i的余数和商。进一步，使用公式 (5.14) 确定 P′c的商。

$$
Q′i= P′i \div 4, \quad \text{and} \quad R′i= P′i \mod 4, \quad (5.13)
$$
$$
Q′c= P′c \div 4. \quad (5.14)
$$

步骤2: 现在使用公式 (5.15) 计算四个差值

$$
d′i= |Q′c −Q′i| \quad \text{for } i= 2,4,6,8. \quad (5.15)
$$

步骤3: 查看表 5.1。d′i落入其某一个范围内。该范围的 HC 为 ti，LB 为 Li。对于 i = 2, 4,6,8, 使用公式 (5.16) 确定 Si。它是 ti个二进制位的十进制值。

$$
Si= d′ i −Li. \quad (5.16)
$$

现在对于 i = 2,4,6,8，将 Si 转换为 ti 个二进制位并追加到 EBDS。

步骤4： 对于 i = 2,4,6,8，将 R′ i 转换为 2 位并追加到 EBDS 中。因此，数据提取的第一阶段完成。

第二阶段的提取过程 应用于像素 P′ 1, P′ 3, P′ 7, 和 P′ 9。该过程在步骤5–7中执行。

步骤5: 像素P′ 1的两个相邻像素是P′ 2和P′ 4。类似地，像素P′ 3的两个相邻像素是P′ 2和P′ 6。像素 P′ 7的两个相邻像素是P′ 4和P′ 8。像素P′ 9的两个相邻像素是P′ 6和P′ 8。计算d′ 1,、d′ 3,、d′ 5,和d′ 7,这 4个差值，使用公式(5.17)。

$$
d′ 1= |P′2 − P′4|, \quad d′ 3= |P′2 − P′6|, \quad d′ 7= |P′4 − P′8|, \quad d′ 9= |P′6 − P′8|. \quad (5.17)
$$

步骤6： 对于 i = 1,3,7,9, 使用公式 (5.18) 计算 ni，如果 ni ≥4，则令 ni= 4。

$$
ni=
\begin{cases}
1 & \text{if } 0 ≤ d′ i ≤ 1, \
\lfloor \log_2 di \rfloor & \text{if } d′ i > 1.
\end{cases}
\quad (5.18)
$$

步骤7： 对于 i = 1,3,7,9, 计算 bi= P′ i模 2ni, 将每个 bi转换为 ni位二进制数据，并附加到 EBDS。因此，提取过程的第二阶段完成。（见图 5.3。）

5.2.3 嵌入与提取示例

考虑图5.4A中所示的示例块。像素的十进制值为P1=100、P2= 101、P3= 102、P4= 101、 Pc= 102、P6= 103、P7= 101、P8= 102和P9= 104。假设要嵌入的秘密数据是 (0111 01 00 01 10 01 00 10 11 1 0 10 1)2。下面逐步说明将该数据嵌入到块中的过程。

88 数字媒体隐写术

5 基于加减的QVD和边匹配的图像隐写术（续）

5.3 实验分析

所提出的隐写技术已在MATLAB® R2015a中编程实现。实验使用了来自SIPI图像数据库的多种图像。[34]表5.2记录了八个样本的结果。图5.5列出了四个测试图像样本，图5.6展示了它们对应的四个隐写图像。这些隐写图像看起来无异常，其中没有任何可见痕迹。

表5.2 所提方案的性能测量。

测试图像 (尺寸 = 512× 512× 3)	PSNR	容量	QI	BPB
Pot	34.30	2,502,088	0.9978	3.18
房子	34.38	2,864,210	0.9961	3.64
Boat	33.36	2,863,565	0.9968	3.64
Jet	34.51	2,727,179	0.9941	3.47
辣椒	33.32	2,714,012	0.9965	3.45
蒂芙尼	33.69	2,727,278	0.9918	3.47
狒狒	32.77	3,190,636	0.9945	4.06
Lena	34.80	2,765,439	0.9969	3.52
平均	33.89	2,794,301	0.9956	3.55

该方案的效率通过三个参数进行衡量。第一个参数是PSNR，用于计算隐写图像的失真程度。第二个重要参数是HC，表示可嵌入图像中的总数据量。有时每字节的HC被称为每字节比特数（BPB）。第三个参数称为质量指数QI，用于估计两幅图像之间的相似性。

PSNR的计算如公式(5.19)所示，其中Pij为原始像素，Qij为隐写像素，m× n表示图像尺寸。对于彩色图像，每个字节可视为一个计算单位，并可应用公式(5.19)。对于图5.5中的测试图像，m = 512和n = 1536。

$$
\text{PSNR} = 10 \times \log_{10} \left( \frac{255 \times 255 \times m \times n}{\sum_{i=1}^{m} \sum_{j=1}^{n}(P_{ij} - Q_{ij})^2} \right). \quad (5.19)
$$

92 数字媒体隐写术

表5.3 各种现有方案与所提方案的性能比较。

隐写技术	平均PSNR	平均HC	平均QI	平均BPB
[7]中的7‐方向PVD	39.78	1,885,371	0.9985	2.39
LSB+PVD 在[16]类型1中	40.11	2,385,386	0.9988	3.03
LSB+PVD 在[16]类型2中	38.57	2,466,275	0.9984	3.13
[29]类型1中的8方向PVD	39.55	2,361,368	0.9986	3.00
[29]类型2中的8方向PVD	37.22	2,603,604	0.9977	3.31
所提出的ASQVD+SM方案	33.89	2,794,301	0.9956	3.55

为了测量QI，可以使用式(5.20)。在式(5.20)中，P和Q分别表示原始图像和隐写图像的平均像素值。

$$
\text{QI} = \frac{4 \times P \times Q \times \left{ \sum_{i=1}^{m} \sum_{j=1}^{n}(P_{ij} - P)(Q_{ij} - Q) \right}}{\left{ \sum_{i=1}^{m} \sum_{j=1}^{n}(P_{ij} - P)^2 + \sum_{i=1}^{m} \sum_{j=1}^{n}(Q_{ij} - Q)^2 \right} \times \left{ (P)^2 + (Q)^2 \right}}. \quad (5.20)
$$

该方案的PSNR、HC、QI和BPB值如表5.3所示。不同技术之间这些参数的比较如表 5.3所示。PSNR和QI的计算是基于隐藏了70万比特数据的隐写图像进行的。从该表中可以看出，我们方案的平均HC为3.55 BPB。技术[7]的平均HC为2.39 BPB。技术[16]的两个变体的平均HC分别为3.03 BPB和3.13 BPB。类似地，技术[29]的两个变体的平均HC分别为 3.00 BPB和3.31 BPB。我们方案的PSNR为33.89 dB，处于{30,40}的可接受范围内。理想情况下，PSNR值大于40 dB的隐写图像是不可察觉的；PSNR低于30 dB的隐写图像由于失真过高而不可接受；PSNR值小于40 dB但大于30 dB的隐写图像失真适中，是可以接受的。

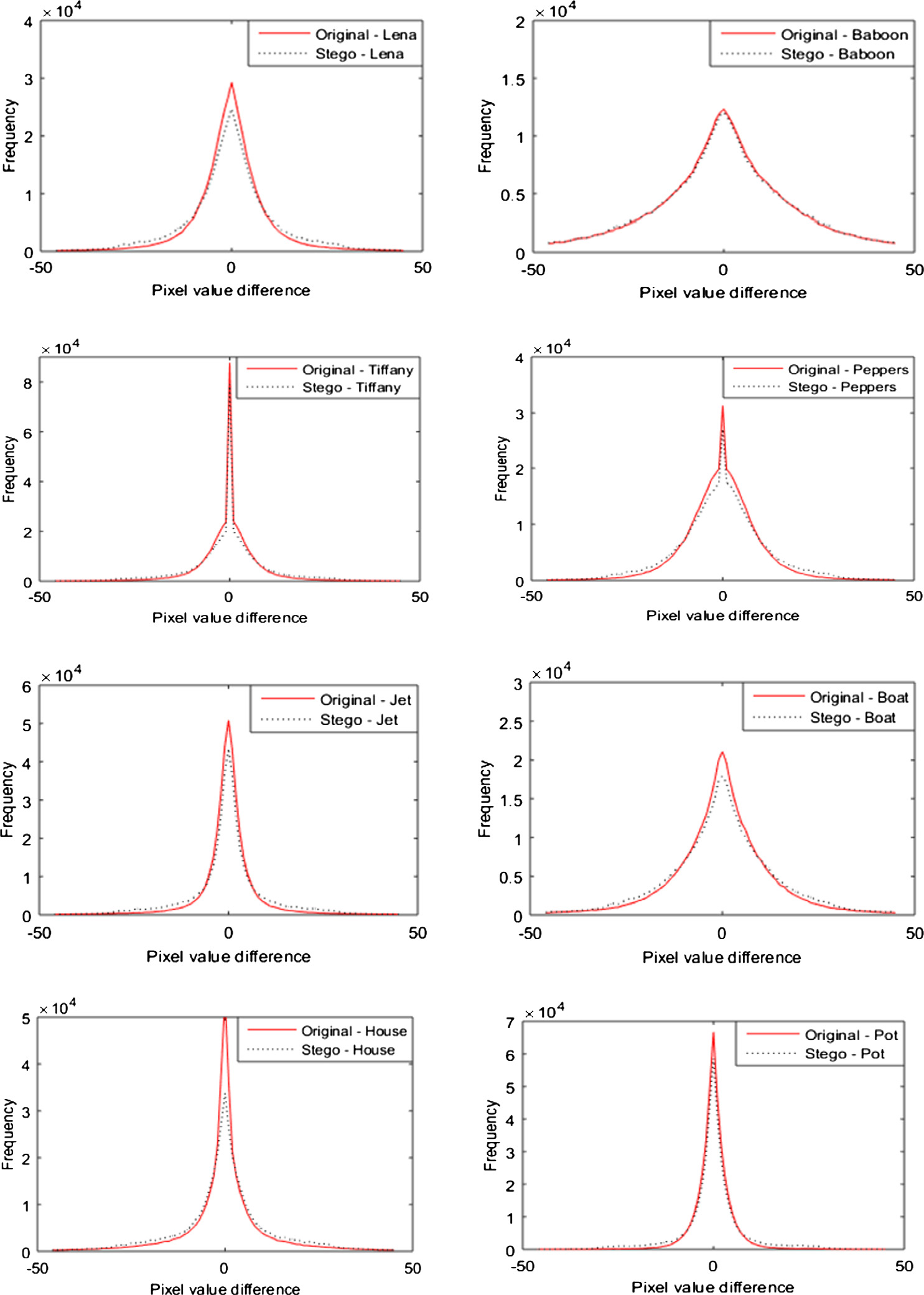
所开发的方案采用了差值和替换的原理。因此，通常通过PDH分析和RS检测来评估其安全性。PDH是一个二维曲线。其中 x轴表示像素差， y轴表示像素差频率[37,38]。研究发现，对于自然图像，PDH曲线具有较平滑的特性，即曲线不会呈现锯齿形状。但在传统 PVD技术的隐写图像中，会出现这种锯齿形状[35]。图5.8展示了八幅测试图像的PDH分析结果。共有八个子图，每幅图像对应一个。在每个子图中，原始图像的PDH用实线表示，隐写图像的PDH用虚线表示。请注意，每个子图中的虚线曲线均无锯齿状外观，这表明PDH检测无法识别所提方案。

The RS测试通过参考四个估计值Rm、R−m、Sm和S−m[36]应用于所提出的技术。步骤如下：将图像M分成fi‐

第 5 •基于加减QVD和边匹配的图像隐写术 93

有限数量的等尺寸块。设G为其中一个块，其组成像素为g1, g2, g3, …, gn。然后使用函数 $ f(g_1, g_2, g_3, …, g_n) = \sum_{i=1}^{n-1} |g_{i+1} - g_i| $ 计算G的平滑度。此外，定义两个函数F1: 2n ↔ 2n + 1和F−1: 2n ↔ 2n −1。F1表示由于最低有效位替换，像素2n变为2n + 1，反之亦然。类似地，F−1表示由于最低有效位替换，像素值2n变为2n−1，反之亦然。然后在M的所有块上应用F1和F−1，利用公式(5.21)–(5.24)解释Rm、Sm、R−m和S−m。

$$
R_m = \frac{\text{No of blocks satisfying the condition } f(F_1(G)) > f(G)}{\text{Total number of blocks}}, \quad (5.21)
$$

$$
S_m = \frac{\text{No of blocks satisfying the condition } f(F_1(G)) < f(G)}{\text{Total number of blocks}}, \quad (5.22)
$$

$$
R_{-m} = \frac{\text{No of blocks satisfying the condition } f(F_{-1}(G)) > f(G)}{\text{Total number of blocks}}, \quad (5.23)
$$

$$
S_{-m} = \frac{\text{No of blocks satisfying the condition } f(F_{-1}(G)) < f(G)}{\text{Total number of blocks}}. \quad (5.24)
$$

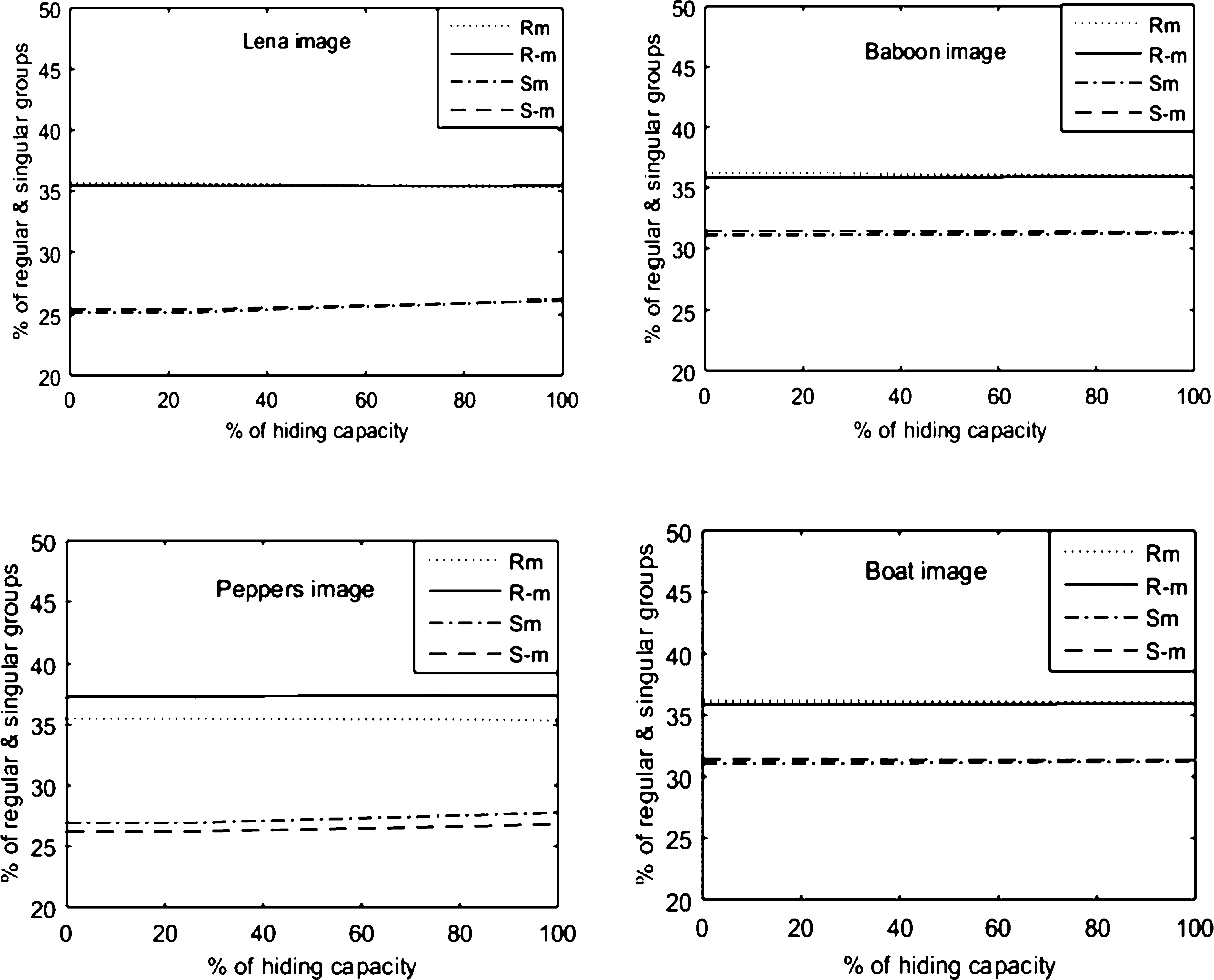
根据RS检测的概念，如果$ R_{-m} - S_{-m} > R_m - S_m $成立，则图像中包含数据。如果$ R_m ≈ R_{-m} > S_m ≈ S_{-m} $成立，则图像中没有数据。图5.9表示四幅图像的RS检测结果。其中有四个子图，每个图像对应一个子图。我们可以观察到Rm接近R−m，并且它们几乎相互平行，这意味着实现了$ R_m ≈ R_{-m} $。类似地，Sm接近S−m，并且它们也几乎相互平行，这意味着实现了$ S_m ≈ S_{-m} $。此外，由Rm或R−m表示的线位于由Sm或S−m表示的线之上。因此我们可以得出结论：$ R_m ≈ R_{-m} > S_m ≈ S_{-m} $成立，这意味着所提方案无法被RS检测发现。

94 数字媒体 隐写术

第 5 •基于加减QVD和边匹配的图像隐写术 95

Lena、(B) 狒狒、(C) 辣椒和(D) 船的分析 图像。)

5.4 结论

本章提出了一种基于ASQVD和SM两种原理的新型隐写机制。该机制在 3 × 3大小的不相交像素块中进行两个阶段的隐藏。在第一阶段，对中心像素及其四个侧向相邻像素（即左、右、下和上相邻像素）执行ASQVD和余数替换。根据这五个像素的新值，在第二阶段对四个角像素采用SM嵌入方法。所开发的方案已在MATLAB中编程实现，并在PSNR、HC和QI方面与相关现有方案进行了比较。从记录的观测结果可以看出，所提出的技术在这些参数值上表现令人满意。此外，我们还注意到，该方案的HC大于相关现有技术的HC。为了评估所提方案的安全性，进行了RS和PDH检测。从实验结果和PDH曲线可以看出，PDH检测无法识别所提出的隐写方案。类似地，从RS曲线可以观察到$ R_m ≈ R_{-m} > S_m ≈ S_{-m} $，因此RS检测也无法识别该方案。