动态规划（一）

动态规划(一)

一个问题可以分解成子问题，通过子问题进行求解
例题1.爬台阶问题：
⚫ TT想去图书馆学习，他现在要爬台阶进去，其中：一共有 n 级台阶，一
步可以走 1 阶或 2 阶，问走到第 n 阶有多少种方案。
⚫ n <= 1000000
⚫ n = 2，ans = 2
⚫ 1+1
⚫ 2
⚫ n = 4，ans = 5
⚫ 1+1+1+1
⚫ 1+1+2
⚫ 1+2+1
⚫ 2+1+1
⚫ 2+2

定义fi --表示走到第i级台阶的方案数

         f1 = 1,f2 = 2
         f i = f i-1 + f i-2 ,i >= 3

方案一递归

int solve(int n){
	if(n==1)
	return 1;
	if(n==2)
	return 2;
	return solve(n-1) + solve(n-2);
}

引入 – 记忆化

int f[maxn];

int solve(int n){
	if(f[n]) return f[n];
	if(n==1) return f[1] = 1;
	if(n==2) return f[2] = 2;
	return f[n] = solve(n-1) + solve(n-2);
}

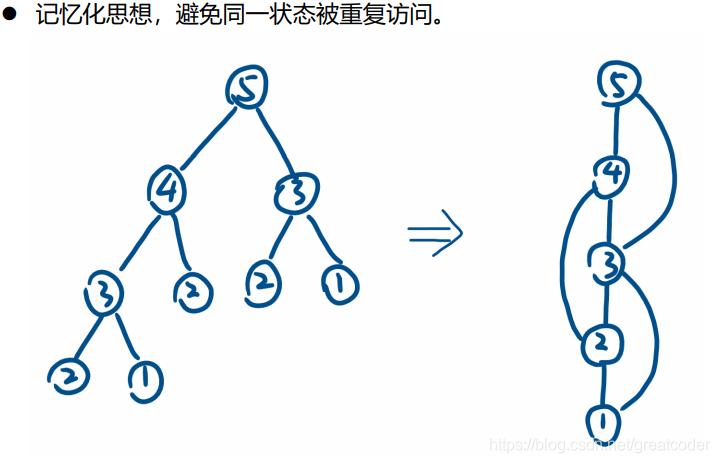
方案二递推

int solve(int n){
    f[1] = 1;
    f[2] = 2;
    for(int i =3 ;i <= n;i++)
    	f[i] = f[i-1] + f[i-2];
    return f[n];
}

动态规划的两种基本思想

带备忘的自顶向下法

按自然递归白那些过程，保存每个子问题的解。当需要一个子问题的解时，检查是否已经保存过此解，若果是，直接返回，否则计算子问题的解。

自底向上法

热河子问题的且介都只依赖于更小的子问题求解。按照从小到大的顺序依次求解子问题的过程。

例题2 爬台阶问题II

还是TT，他要去 N3 楼做实验，要爬台阶到三楼，其中一共有 n 级台阶，
一步可以走 1, 2, 3, …, k 阶，诶，同时有些台阶不能落脚，问走到第 n 阶
的方案数。
⚫ n <= 1000000
⚫ n = 4，不能落脚的台阶 = [2], k = 2, ans = 1
⚫ 0→1→3→4
⚫ n = 5，不能落脚的台阶 = [2], k = 3, ans = 5
⚫ 0→1→3→4→5
⚫ 0→1→3→5
⚫ 0→1→4→5
⚫ 0→3→4→5
⚫ 0→3→5

定义f i 为走到第 i 级台阶的方案数

初始化 f 0 = 1；
转移过程 ： f i = sum(f j) （i - k <= j < i , 当第 j 级台阶可以落脚时）
对于不能落脚的台阶 f i = 0; 表示可以通往此台阶的方案数为 0

例题3 最大区间和

⚫ N 个数字，每个数字∈[-1e9,1e9]，TT想选定一个区间使得和最大，求这
个和。
⚫ [1,2,3,4,5] → [1,2,3,4,5]
⚫ [1,2,-100,4,5] → [1,2,-100,4,5]
⚫ n <= 1000000

贪心，使用前缀和

ans = sum[R] - sum[L - 1];
用一个变量minX 维护R之前的所有的sum中的最小值， SUM[R] - minX为 R位置的最优解。
可以通过方法O（n）求解答案

动态规划

因为区间是连续的，当考虑一个数时，要么将这个数加入之前区间的尾部，要么以这个数单独作为区间的开头。找到一个连续的和最大的区间

定义状态dp i 以 i 位置为区间右端点时，可以取到的最大和

dp i = max(dp i-1 + ai , ai )
仔细分析：当遇到一个数 ai，如果说之前的区间的和为负， 那么把这个数加入之前的区间得到的新的和 X1， 和把这个数作为一个区间的起始相比，肯定是将这个数作为区间的起始得到的结果要大。
考虑对后面的数求和的影响，如果不管我们选择了哪一个，对于后面的数这都是最优的选择。用一个较大的值，和后面的连续的数相加，才能得到较大的结果。

例题4 最大区间和II：

在 例题3 的基础上，TT会一个魔法，使得其中一个数变成 X，如果这个魔
法至多能使用 1 次，求答案。
⚫ X = 100，[1,2,3,4,5] → [100,2,3,4,5]
⚫ X = 100，[1,2,-100,4,5] → [1,2,100,4,5]
⚫ n <= 1000000

定义dp i,0 – 表示 i 为右端点，并且没有使用魔法时，可以取到的最大和

定义dp i ,1 – 表示 i 为右端点，并且使用魔法时，可以取到的最大和

状态转移方程

dp i,0 = max( dp i-1,0 + ai , ai )

dp i, 1 从dp i - 1 没有使用过魔法转移过来，和使用魔法过转移过来
dp i - 1,1 之前已经使用过魔法，dp i -1 ,0 之前没有使用故过
dp i,1 = max( dp i-1,1 + ai, ai, dp i-1,0 + x , x )
答案是 max ( dp[ i ][ 0] , dp [ i ] [ 1] )

动态规划常用于解决统计类问题（统计方案总数）和最优值问题（最大值或最小值），尤其普遍适用于最优化问题

动态规划问题的特征

一、最优子结构

二、重叠子问题

三、无后效性原则

动态规划步骤：

1. 分析题目特性，转化为抽象模型（找出最优解的性质）；
2. 设计动态规划方程；
3. 定义初始化条件；
4. 以自底向上（递推）或带备忘的自顶向下（记忆化搜索）的方式进行计算；
5. 统计答案并输出。

for U取遍所有状态 do //枚举状态
for X取遍所有决策 do //枚举决策
// 状态转移

动态规划常见模型

⚫ 线性型
⚫ 坐标型
⚫ 背包型
⚫ 区间型
⚫ 状态压缩型
⚫ 树型
⚫ 矩阵型

例题5 走地图

TT在一个 n×m 的地图上，起点为左下角，终点为右上角，TT只能向右或
向上行走，询问走到终点的方案数。
⚫ n,m <= 1000
⚫ （其实可以通过排列组合解决，可以自行思考）
⚫ 假定有些点存在障碍物而不可行走，又应当如何设计？

定义状态 ：f [ i ] [ j ] 表示从起点，到 （ i ，j ）点的方案数。

状态转移：f [ i ][ j ] = f [ i -1][ j ] + f [ i ][ j - 1] (当 （i-1，j）（i，j-1）合法时)

初始化 f [ 1 ][ 1 ] = 1
输出答案 f 【n】【m】

例题6 拿数问题

给 n 个数，每一步能拿走一个数，比如拿第 i 个数， Ai = x，得到相应的
分数 x，但拿掉这个 Ai 后，x+1 和 x-1 (如果有 Aj = x+1 或 Aj = x-1 存在) 就
会变得不可拿（但是有 Aj = x 的话可以拿这个 x）。求最大分数。
⚫ n, Ai <= 100000

题意说的不明白，比如有四个数 98 99 100 99 ，拿了99，有两个99都可以拿，但是98 ，100不可以拿， 因为 98 = 99 - 1， 100 = 99 +1

解决方案，定义一个数组cnt[MAXN] ,cnt[i]表示序列中 i 的个数，对cnt[i]进行dp

定义dp[i]为考虑值为 1 - i的所有的数，能求得的最大值

状态转移方程

dp[ i ] = max( dp[ i - 2] + i * cnt [ i ] , dp[ i -1 ])
输出答案dp[ n ]

例题7 弹钢琴

一段旋律中的每个音符都可以用一个小写英
文字母表示。当组成一段旋律的字符 ASCII码是非递减的，旋律被称为是
高昂的，例如 aaa,bcd.
现在TT已经学会了 n 段高昂的旋律，他想利用它们拼接处一个尽可能长
的高昂的旋律，问最长长度是多少？(n<=1e6, 字符串长度和 <=1e6)
⚫ 5
bcdefhijk
bcd
aaa
eeeefghhh
zzzz
⚫ 答案是 19（aaa, bcd, eeeefghhh, zzz）

例题8. 矩阵选数（作业） ：

⚫ 发现每一列只会和前一列关联
⚫ 定状态：定义 dp[i][0/1/2] 表示仅考虑前 i 列，并且第 i 列选的是第 0/1/2
数的最小答案 。
⚫ 状态转移方程为：
⚫ dp[i][0]=min(dp[i-1][0]+|a[0][i]-a[0][i-1]|,
dp[i-1][1]+|a[0][i]-a[1][i-1]|,
dp[i-1][2]+|a[0][i]-a[2][i-1]|)
⚫ 其他两个转移方程 dp[i][1]、dp[i][2] 同理
⚫ 初始化：dp[][]=INF, dp[1][0/1/2]=0
⚫ 输出答案：max{dp[n][i], 0<=i<=2}