深度学习基础算法-神经网络之激活函数_将网络结构中的权重改为激活函数-优快云博客

本文链接：https://blog.youkuaiyun.com/gracejpw/article/details/103060765

本文深入解析神经网络算法，探讨其在深度学习与人工智能领域的核心作用。从感知机到多层感知机，再到神经网络的结构与工作原理，文章详细介绍了激活函数如sigmoid与ReLU的应用，并对比了它们与阶跃函数的区别。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

神经网络算法

神经网络算法试图模拟生物神经系统的学习过程，以此实现强大的预测性能。不过由于是模仿人类大脑，所以神经网络的模型复杂度很高也是众所周知。在现实应用中，神经网络可以说是解释性最差的模型之一，商业环境中很少使用神经网络。然而除了商业分析，还有许多算法应用的部分，其中最重要的是深度学习和人工智能的领域，现在大部分已经成熟的人工智能技术：图像识别，语音识别等等，背后都是基于神经网络的深度学习算法。因此，作为机器学习中（可能是）最复杂的，深度学习中基础的算法，神经网络的了解和学习是很有必要的。

从感知机到神经网络

神经网络与多层感知机还是有一点区别的。用图来表示神经网络的话，如下图所示。我们把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层（有的教材也称为隐藏层）。所谓"隐藏"的意思，在这里面的神经元我们是看不见的。我们把下图的三层依次称为第0层，第1层，第2层，分别对应输入层，中间层，输出层。
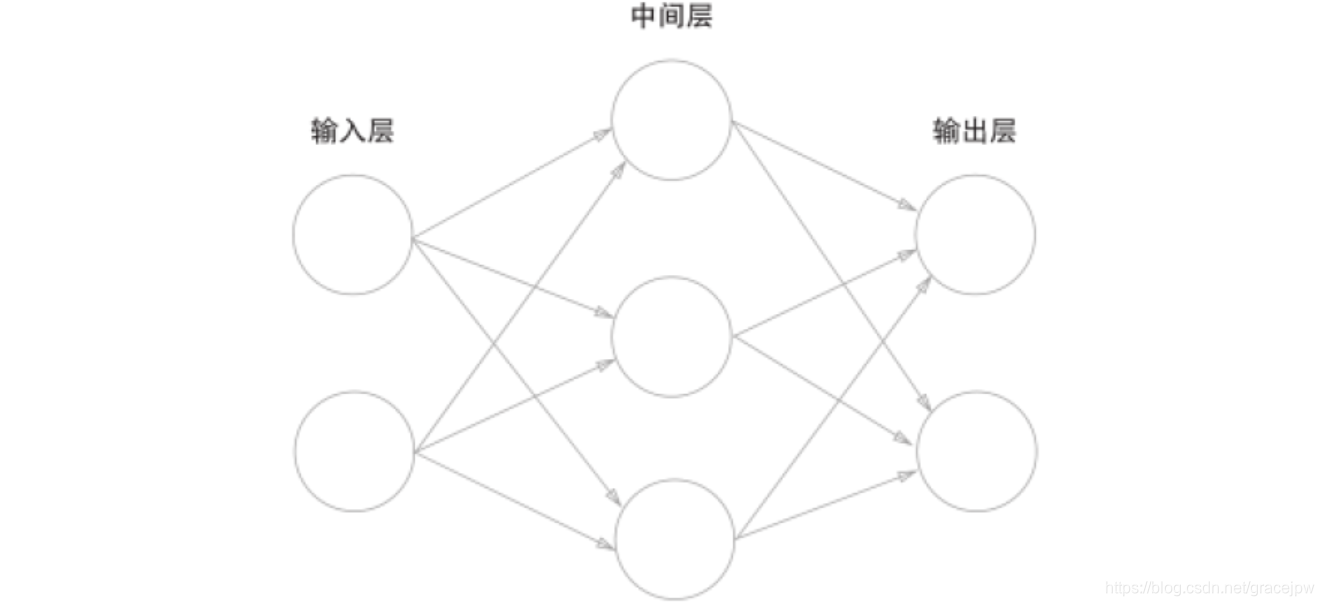
在这里插入图片描述
单就神经网络的这种连接方式，和之前的感知机是没有任何差别的。感知机的公式:

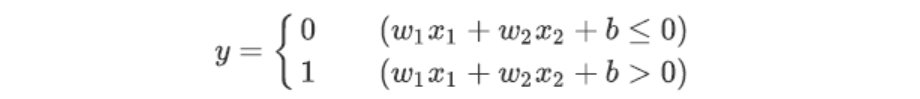
在之前的图片中，偏置并没有在图像中显示出来，我们可以把图片改成下图来表示权重，它对应的输入信号固定为1。
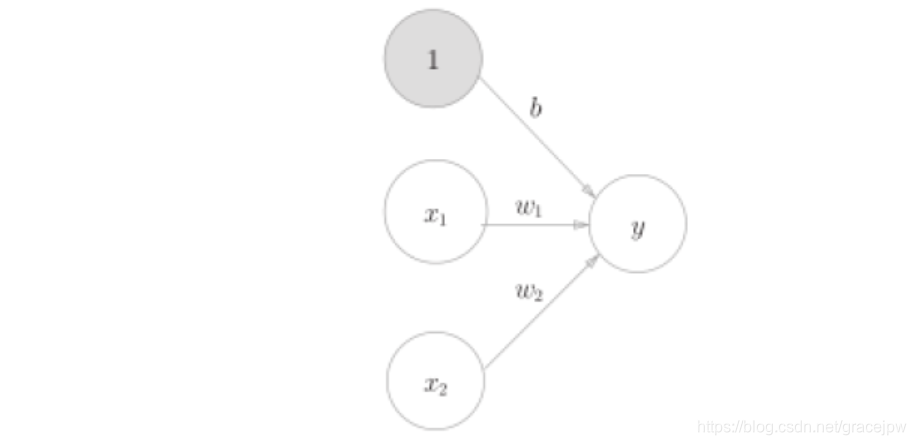
在这里插入图片描述
这个感知机将x₁ 、x₂、1 三个信号作为神经元的输入，将其和各自的权重相乘后，传送至下一个神经元。在下一个神经元中，计算这些加权信号的总和。如果这个总和超过0，则输出1，否则输出0。而偏置部分的信号始终是1，是不变的。现在，我们为了能够进一步简化公式，为之后使用线性代数计算更方便，我们把公式再一次进行改造：
$y=h(b+ω_1x_1~+ω_2x_2)$
而h(x)就应该是这样的:
$0x⩽01x⩾0h(x)=\left\{ \begin{array}{ll} 0 & x \leqslant 0\\1 & x \geqslant 0 \end{array} \right.$