LogisticRegression类的格式
sklearn.linear_model.LogisticRegression (penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100, multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)
重要参数penalty & C
正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数ω向量的L1范式和L2范式的倍数来实现。这个增加的范式,被称为“正则项”,也被称为"惩罚项"。
损失函数改变,基于损失函数的最优化来求解的参数取值必然改变,以此来调节模型拟合的程度。其中L1范式表现为参数向量中的每个参数的绝对值之和,L2范数表现为参数向量中的每个参数的平方和的开方值。
J(ω)L1=C∗J(ω)+∑j=1n∣ωj∣(j≥1)J(\omega)_{L1}=C*J(\omega)+\sum_{j=1}^n|\omega_j|\quad (j\ge1)J(ω)L1=C∗J(ω)+j=1∑n∣ωj∣(j≥1)
J(ω)L2=C∗J(ω)+∑j=1n∣ωj∣2(j≥1)J(\omega)_{L2}=C*J(\omega)+\sqrt{\sum_{j=1}^n|\omega_j|^2}\quad (j\ge1)J(ω)L2=C∗J(ω)+j=1∑n∣ωj∣2(j≥1)
其中J(ω)是损失函数,C是用来控制正则化程度的超参数,n是方程中特征的总数,也是方程中参数的总数,j代表每个参数。j要大于等于1,是因为参数向量中,第一个参数是截距ω0,其通常不参与正则化。
许多书籍中也有如下的写法:
J(ω)L1=J(ω)+12b2∑j∣ωj∣J(\omega)_{L1}=J(\omega)+\frac1{2b^2}\sum_j|\omega_j|J(ω)L1=J(ω)+2b21j∑∣ωj∣
J(ω)L2=J(ω)+ωTω2σ2J(\omega)_{L2}=J(\omega)+\frac{\omega^T\omega}{2\sigma^2}J(ω)L2=J(ω)+2σ2ωTω
其实和上面展示的式子本质一样。不过在大多数教材和博客中,常数项是乘以正则项,通过调控正则项来调节对模型的惩罚。
而sklearn当中,常数项C是在损失函数的前面,通过调控损失函数本身的大小,来调节对模型的惩罚。
参数说明
penalty
可以输入"l1"或"l2"来指定使用哪一种正则化方式,不填写默认"l2"。
注意,若选择"l1"正则化,参数solver仅能够使用求解方式”liblinear"和"saga“,若使用“l2”正则化,参数solver中所有的求解方式都可以使用。
注:
solver:优化算法选择参数,有五个可选参数,即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了对逻辑回归损失函数的优化方法:
liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅用一部分的样本来计算梯度,适合于样本数据多的时候。
saga:快速梯度下降法,线性收敛的随机优化算法的的变种。
C
C正则化强度的倒数,必须是一个大于0的浮点数,不填写默认1.0,即默认正则项与损失函数的比值是1:1。C越小,损失函数会越小,模型对损失函数的惩罚越重,正则化的效力越强,参数会逐渐被压缩得越来越小。
L1正则化和L2正则化虽然都可以控制过拟合,但效果并不相同。当正则化强度逐渐增大(即C逐渐变小),参数的取值会逐渐变小,但L1正则化会将参数压缩为0,L2正则化只会让参数尽量小,不会取到0。
在L1正则化在逐渐加强的过程中,携带信息量小的、对模型贡献不大的特征的参数,会比携带大量信息的、对模型有巨大贡献的特征的参数更快地变成0,所以L1正则化本质是一个特征选择的过程,掌管了参数的“稀疏性”。L1正则化越强,参数向量中就越多的参数为0,参数就越稀疏,选出来的特征就越少,以此来防止过拟合。因此,如果特征量很大,数据维度很高,我们会倾向于使用L1正则化。由于L1正则化的这个性质,逻辑回归的特征选择可以由Embedded嵌入法来完成。
注:Embedded嵌入法
嵌入法是一种让算法自己决定使用哪些特征的方法,即特征选择和算法训练同时进行。
在使用嵌入法时,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性,比如决策树和树的集成模型中的feature_importances_属性,可以列出各个特征对树的建立的贡献,可以基于这种贡献的评估,找出对模型建立最有用的特征。
因此,相比于过滤法,嵌入法的结果会更加精确到模型的效用本身,对于提高模型效力有更好的效果。并且,由于考虑特征对模型的贡献,因此无关的特征(需要相关性过滤的特征)和无区分度的特征(需要方差过滤的特征)都会因为缺乏对模型的贡献而被删除掉,可谓是过滤法的进化版。
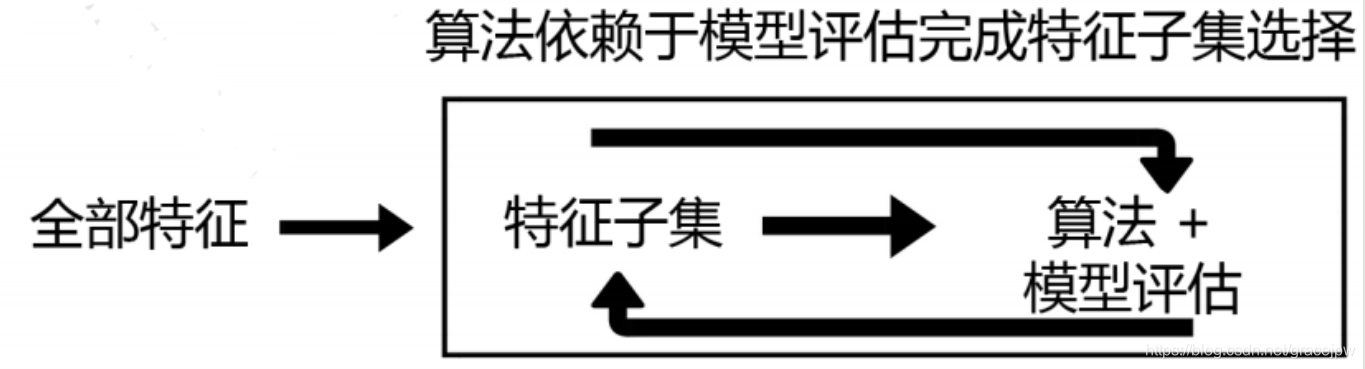
过滤法中使用的统计量可以使用统计知识和常识来查找范围(如p值应当低于显著性水平0.05),而嵌入法中使用的权值系数却没有这样的范围可找——可以说,权值系数为0的特征对模型丝毫没有作用,但当大量特征都对
模型有贡献且贡献不一时,很难去界定一个有效的临界值。此时,模型权值系数就是我们的超参数,或许需要学习曲线,或者根据模型本身的某些性质去判断这个超参数的最佳值究竟应该是多少。
*以上关于“Embedded嵌入法”的内容引自:https://www.cnblogs.com/zhange000/articles/10751525.html
相对的,L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大的特征的参数会非常接近于0。通常,如果主要目的只是为了防止过拟合,选择L2正则化就足够了。但是如果选择L2正则化后还是过拟合,模型在未知数据集上的效果表现很差,就可以考虑L1正则化。
而两种正则化下C的取值,都可以通过学习曲线来进行调整。
建立两个逻辑回归,L1正则化和L2正则化的差别一目了然:
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
data = load_breast_cancer()
X = data.data
y = data.target
data.data.shape
lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)
#逻辑回归的重要属性coef_,查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_
array([[ 3.98998625, 0.03175695, -0.13568613, -0.01621048, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.50488002, 0. , -0.07129652, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , -0.245602 , -0.12839197, -0.01441751, 0. ,
0. , -2.05368234, 0. , 0. , 0. ]])
lrl2 = lrl2.fit(X,y)
lrl2.coef_
array([[ 1.61543234e+00, 1.02284415e-01, 4.78483684e-02,
-4.43927107e-03, -9.42247882e-02, -3.01420673e-01,
-4.56065677e-01, -2.22346063e-01, -1.35660484e-01,
-1.93917198e-02, 1.61646580e-02, 8.84531037e-01,
1.20301273e-01, -9.47422278e-02, -9.81687769e-03,
-2.37399092e-02, -5.71846204e-02, -2.70190106e-02,
-2.77563737e-02, 1.98122260e-04, 1.26394730e+00,
-3.01762592e-01, -1.72784162e-01, -2.21786411e-02,
-1.73339657e-01, -8.79070550e-01, -1.16325561e+00,
-4.27661014e-01, -4.20612369e-01, -8.69820058e-02]])
可见,当选择L1正则化的时候,许多特征的参数都被设置为了0,这些特征在真正建模的时候,不会出现在模型中,而L2正则化则是对所有的特征都给出了参数。
究竟哪个正则化的效果更好呢?还是都差不多?
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest =
train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1,19):
lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
lrl1 = lrl1.fit(Xtrain,Ytrain)
l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):
plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例例的位置在哪⾥里里?4表示,右下⻆角
plt.show()
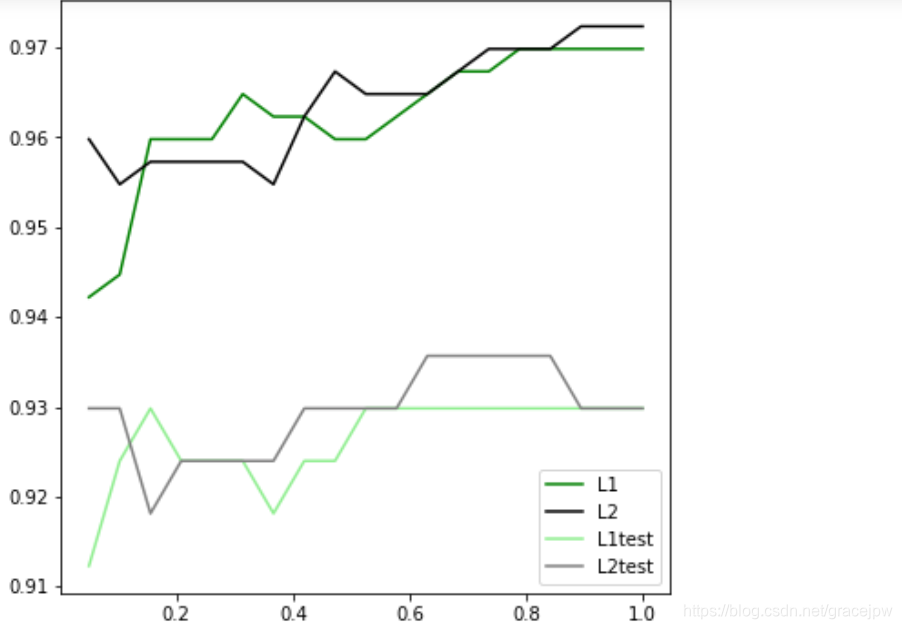
可见,至少在乳腺癌数据集下,两种正则化的结果区别不大。但随着C的逐渐变大,正则化的强度越来越小,模型在训练集和测试集上的表现都呈上升趋势,直到C=0.8左右,训练集上的表现依然在走高,但模型在未知数据集上的表现开始下跌,这时候就是出现了过拟合。可以认为,C设定为0.8比较好。实际工作中,默认使用L2正则化,如果感觉模型效果不好,就换L1试试。








 本文介绍了sklearn的LogisticRegression模型中,正则化参数penalty(L1或L2)和C的含义及作用。C是正则化强度的倒数,控制模型对损失函数的惩罚程度。L1正则化导致参数稀疏,适用于特征选择;L2正则化则让所有特征都有小的贡献,防止过拟合。选择合适的C值可以通过学习曲线来确定。
本文介绍了sklearn的LogisticRegression模型中,正则化参数penalty(L1或L2)和C的含义及作用。C是正则化强度的倒数,控制模型对损失函数的惩罚程度。L1正则化导致参数稀疏,适用于特征选择;L2正则化则让所有特征都有小的贡献,防止过拟合。选择合适的C值可以通过学习曲线来确定。
















 8101
8101










