机器学习：基于原型的聚类技术K-Means_机器学习中原型网络中计算全局质心的方法-优快云博客

本文链接：https://blog.youkuaiyun.com/gracejpw/article/details/102552964

本文介绍了基于原型的聚类，特别是K-Means算法。K-Means通过寻找最优质心来划分数据，其中质心可以是簇中点的平均值。算法执行包括选择初始质心，然后不断迭代更新质心和重新分配点。距离衡量部分讨论了数据距离（如欧氏距离、曼哈顿距离和余弦相似性）和文本距离。误差平方和（SSE）是聚类效果的重要指标，目标是找到最小化SSE的模型。聚类目标函数和质心计算方法与所选距离度量和邻近度函数密切相关。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

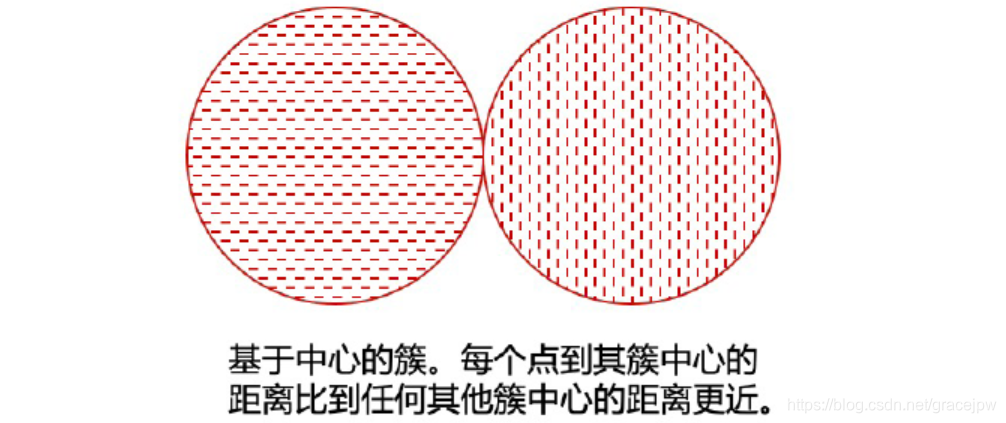
基于原型的簇

此时簇是对象的集合，并且其中每个对象到定义该簇的原型的距离比到其他簇的原型的距离更近（或更加相似）。对于具有连续属性的数据，簇的原型通常是质心，即簇中所有点的平均值。当质心没有意义时（例如当数据具有分类属性时），原型通常是中心点，即簇中最有代表性的点。对于许多数据类型，原型可以视为最靠近中心的点；在这种情况下，通常把基于原型的簇看作基于中心的簇（center-based cluster）。毫无疑问，这种簇趋向于呈球状。下图是一个基于中心簇的例子。
在这里插入图片描述

K-Means

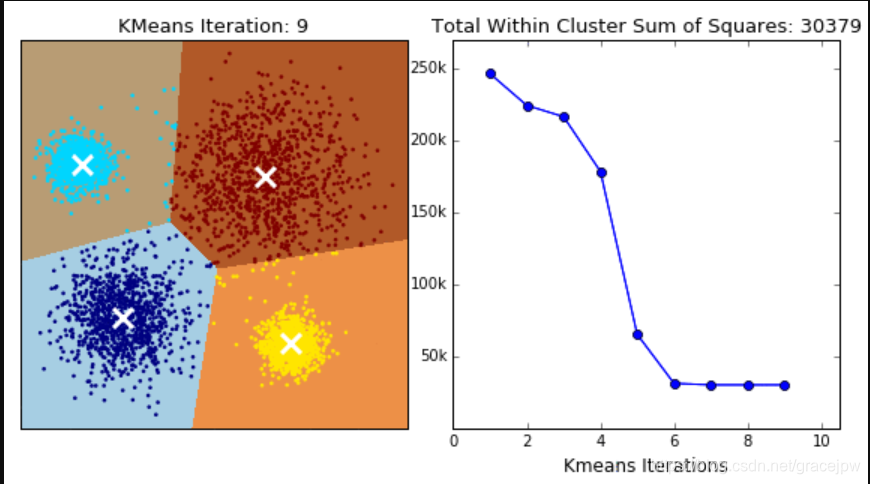
K均值算法比较简单，从介绍它的基本算法开始。首先，选择K个初始质心，其中K是我们指定的参数，即所期望的簇的个数。每个点指派到最近的质心，而指派到一个质心的点集为一个簇。然后，根据指派到簇的点，更新每个簇的质心。重复指派和更新步骤，直到簇不发生变化，或等价地，直到质心不发生变化。
K-Means的核心任务就是根据我们设定好的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下：
在这里插入图片描述
什么情况下，质心的位置不再变化呢？当我们找到一个质心，在每次迭代中被分配到这个质心上的样本都是一致的，即每次新生成的簇都是一致的，所有的样本点都不会再从一个簇转移到另一个簇，质心就不会变化了。
在这里插入图片描述